DeepLearning与CNN入门基础总结

原创

已于 2022-05-17 21:15:31 修改 · 1.3k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#cnn #python #人工智能 #深度学习 #图像处理

于 2022-05-17 21:15:01 首次发布

由于想入门深度学习的一些框架，所以就自己开始学习了关于深度学习的入门知识以及python代码的实现过程。对于下面的文章的基础是掌握一定的python还有numpy的技巧。而且这篇文章真的是像我这种没有接触过的入门者而言，所以对于掌握很多东西的大佬就可以没有必要看我这篇文章了。

神经网络可能大家听起来确实是一个有挑战性的事情，其实它的本质是一个线性回归以及逻辑回归的问题。那么我们回过头看看机器学习的流程：数据获取->特征工程->建立模型->评估与应哟。

那么深度学习是在干什么的：

其实深度学习一直在做的事情就是提取特征，我们可以称之为特征工程，那么特征工程的作用：

数据特征决定了模型的上限
预处理和特征提取是最核心的
算法与参数选择决定了如何逼近这个上限

那么这一切从一个感知机开始说起：

0x01 从感知机开始

感知机：接收多个输入信号，输出一个信号。感知机的信号只有0和1，表达不传递信号以及传递信号。其实到最后会发现其实感知机就是我们的一个神经单元。

下面是一个接收两个输入信号的感知机的例子：

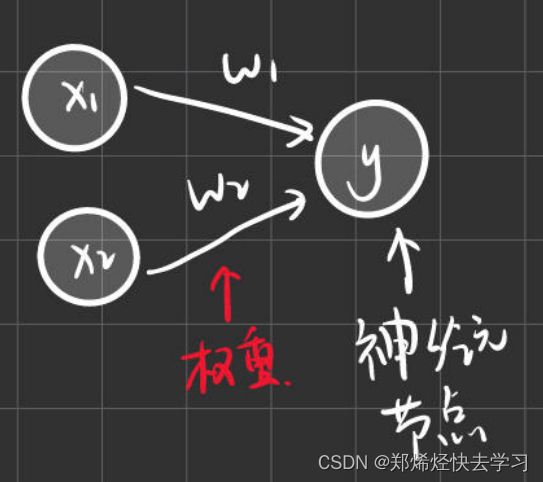
输入信号被送往神经元时，会被分别乘以固定的权重(w1x1,x2w2)。神经元会计算传送过来的信号的总和，只有当这个总和超过了某个界限时才会输出1。这里称为“神经元激活”，并且我们将这个界限称为阈值。

那么使用数学表达式来表达上面那个东西：

感知机的多个输入信号都有各自固定的权重，这些权重都控制着各自信号的重要性作用，权重越大，对应该权重的信号的重要性就越高。

我们先回顾一下关于简单逻辑电路：

与门：x1和x2同时为1时，信号加权总和才会超过给的阈值。
与非门：颠倒了与门的输出。
非门：把实现与门的参数值的符号取反。

以上，感知机可以通过适当地调整参数即可改变其门的表达形式。需要注意的时感知机无法表达异或门。

那么我们可以首先写一个python函数来实现刚刚的逻辑电路AND：

def AND(X1,X2):
    W1,W2,theta = 0.5,0.5,0.7
    tmp=x1*w1+x2*w2;
    if tmp<=theta:
        return 0;
    elif tmp>theta:
        return 1;

那么我们因此可以倒入权重和偏置这么两个概念：

我们可以利用numpy去实现上面的那个功能np.sum(w*x)，最后得到的就是各个元素的总和。

要实现那个上面的公式，我们可以使用如下：tmp=np.sum(w*x)+b

那么对于参数w1、w2、b：

w1、w2：控制输入信号的重要性参数

b：偏置是调整神经元被激活的容易程度（输出信号为1的容易程度）

感知机的局限性就在于它只能表示由一条直线分割的空间，对于弯曲的曲线，是无法使用感知机表示的。

非线性空间：由曲线分割而成的空间。

线性空间：由直线分割而成。

可是在实际的神经网络中，我们不可能让一个网络是线性的性质。

我们可以使用多重感知机来实现异或门的操作：

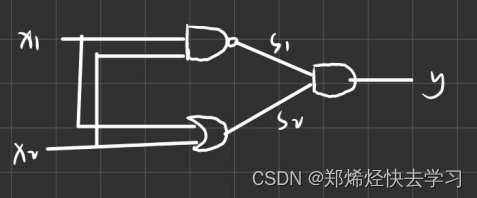
在python中有实现与非门等语句：

AND(x1,x2)	#与门
NAND(x1,x2) #与非门
OR(x1,x2)	#或门

异或门是一种多层结构的神经网络，也就是多层感知机。那么使用代码可以如下表示：

def XOR(x1,x2):
	s1=NAND(X1,X2)
	S2=OR(x1,x2)
	y=AND(s1,s2)
	return y

实际上，与门、或门是单层感知机，而异或门是2层感知机。叠加了多层的感知机也称为多层感知机。单层感知机只能表示线性空间，而多层感知机可以表示非线性空间；多层感知机理论上可以表示计算机。

0x02 从感知机到神经网络

对于复杂的神经网络，感知机也隐含着能够表示它的可能性。那为什么要引入神经网络，对于我们上面感知机，它是需要人工设定权重的工作，即需要人工的确定合适的、能符合预期的输入与输出的权重。那么神经网络重要的性质，就是可以自动从数据中学习到合适的权重参数。

对于神经网络的表示：最左边为输入层，最右边为输出层，中间称为隐藏层。

那么我们回到我们最熟悉的感知机上，我们使用一个神经网络来表示我们的函数：

对于w的初始化可以为一个随机的参数，之后我们要进行不断地更新，使其可以达到我们所预期的值。其实这个处理的函数我们称之为线性函数y=wx+b。

看看下面这幅图：

上面的图像使用的是一个[3,4]的矩阵，也就是权重w，输入一副图像x，之后再加上一个偏置b。最后矩阵的计算可以表达为如下：[3,4] * [4,1] + [3,1] = [3,1]。而且我们可以发现，我们要输出的矩阵的大小，是与偏置b的大小可以说是一样的。

对于我们函数的输出，其实需要一个函数h(x)进行转换，那么这个h(x)就是我们经常听到的激活函数。为什么要使用激活函数呢，因为我们使用了线性的函数进行输出，可是我们使用那么多线性权重去计算，我们要实现一个函数xw1w2w3，那我们为什么不做一个一个权重w4直接等于w1w2w3呢？其实这种线性的处理，在神经网络中是不可取的，我们需要在一次线性函数的输出后，将其转化为非线性输出，这个时候就需要激活函数。

0x03 激活函数

激活函数可以说是连接感知机和神经网络的桥梁了。我们熟悉的神经网络有Relu、Sigmoid等。

朴素的感知机：单层网络，激活函数使用的是阶跃函数的模型。
多层感知机：神经网络，采用sigmoid函数等平滑的激活函数的多层函数。

使用激活函数就开始说明我们已经进入神经网络的世界了。激活函数是为了进行信号转换，转换后的信号即传递给下一个神经元。

sigmoid函数

这个函数的表达式如下：

若使用numpy进行表达是如下的：

def sigmoid(x):
	return 1/(1+np.exp(-x))

阶跃函数

这个函数是最为简单的函数，其解释为当输入超过0时，输出1，否则输出0。

def step_function(x):
    if x>0:
        return 1;
    else:
        return 0;

这里的参数只可以接收实数或者是浮点数，那么对于数组怎么实现：

def step_function(x):
    y = x > 0;					#返回bool类型的数组
    return y.astype(np.int)		#进行类型转换，将bool转为int

也可以将上述合并为如下：

def step_function(x):
	return np.array(x>0,dtype=np.int)

那么对于阶跃函数以及sigmoid函数的区别可以如下：

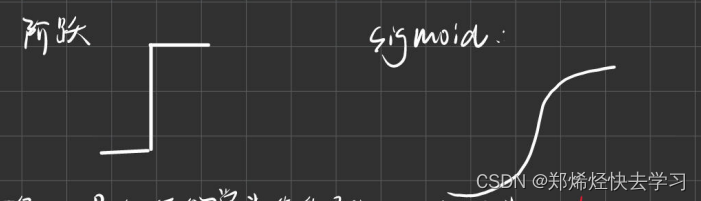
两个函数的平滑性不同，sigmoid是一条平滑的曲线，输出随着输入发生连续的变化。而阶跃函数以0为界，输出发生急剧性变化。sigmoid函数的平滑性对神经网络的学习具有重要意义。

输出值是输入值的常数倍的函数称为线性函数，h(x)=cx。否则就为非线性函数。

神经网络的激活函数必须使用非线性函数。如果使用线性函数，则不管怎么加深层数，总是存在与之等效的“无效”隐藏层的神经网络。因为对于一个线性函数，加深层只会让它一直在乘以一个常数，最后输出一直为y=ax，这根本无法满足叠加层所带来的优势。

ReLu函数

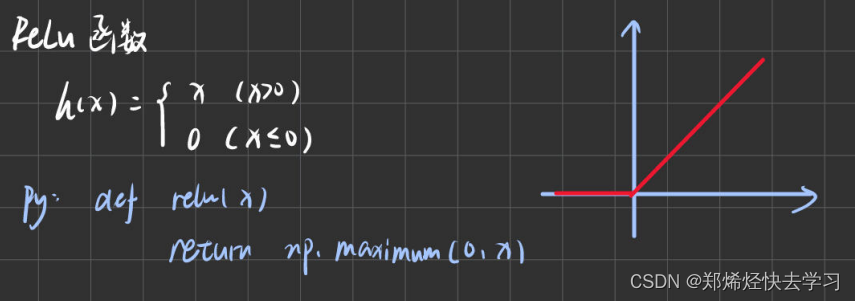
这个函数是比较常用的，现在还在继续使用，对于上面的sigmoid函数，当他遇到大数据的处理时，容易出现数据无法实现更新的情况，就是他曲线上面的那一段平滑的线。比较实用的还是relu函数。

0x04 实现三层神经网络

在实现三层神经网络之前，我们需要了解清楚numpy的一些处理机制，对于多维数组的运算：

数组维度可以使用numpy中np.ndim()进行获取。
数组的形状可以使用A.shape()，返回值为元组，若为一维数组则使用A.shape[0]
实现矩阵间的点积计算：np.dot(A,B)，此函数的使用前提是A列=B行，运算结果C为矩阵A的行数和矩阵B的列数构成。

>>> B=np.array([[1,2],[3,4],[5,6]])
>>> printf(B)
[[1 2]
 [3 4]
 [5 6]]
 >>> np.ndim(B)
 2
 >>> B.shape
 (3,2)

那么我们先看一下三层神经网络的结构：

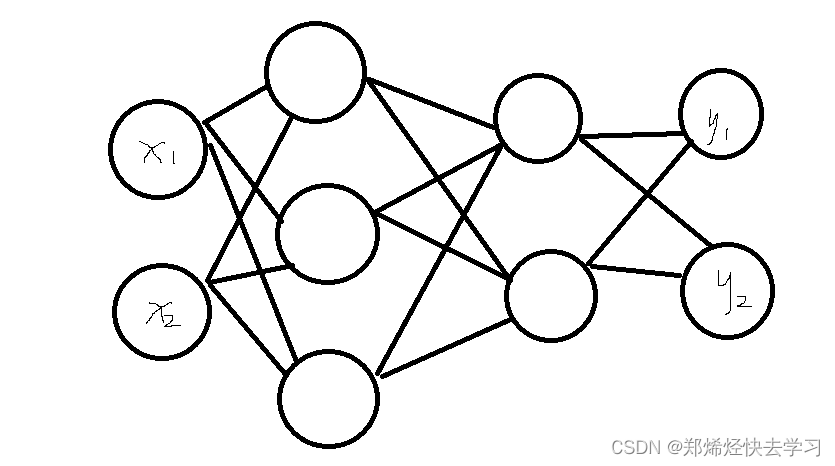
三层神经网络：输入层（第0层）有两个输入的神经元，第一个隐藏层（第1层）有三个神经元，第二个隐藏层（第2层）有两个神经元，输出层（第3层）有两个神经元。

上面的前三层，我们都加上一个偏置b：

那么我们输入层到第一层的第一个神经元的信号传递过程可以表示为如

最低0.47元/天解锁文章