《统计学习方法——感知机》学习笔记

  去年的时候，选修过《机器学习》这门课程，学习过后，很多知识不理解。最近重新学习机器学习的知识，在实验室找到一本前辈们留下的机器学习理论书籍《统计学习方法》，这次打算留下点学习痕迹，做个笔记，方便日后复习。

1.感知机模型

1.1预备知识

  感知机是一个线性的二分类模型，该模型的目的是在输入空间中找到一个超平面S，将输入空间中的样本实例分成正、负两个类别。其中感知机的输入为特征向量，输出为实例的类别，即+1和-1两个值。

1.2 感知机模型定义

  我们首先来定义一下什么是感知机。输入空间是 $X\subseteq {\mathbb{R}}^n$，输出空间是 Y = { + 1 , − 1 } Y=\{+1,-1\} Y={+1,−1}，输入$x\in X$表示实例的特征向量，对应于输入空间的点；输出$y\in Y$表示实例的类别。则感知机可以被定义为如下函数：
$$f(x)=sign(w\cdot x+b)\text{\hspace{1em}(1)}$$
q其中w和b为感知机参数，w为权值（weight），b为偏置（bias）。sign为符号函数：
$$sign(x)=\{\begin{array}{l}+1,x\ge 0\\ \\ -1,x<0\end{array}\text{\hspace{1em}(2)}$$
  感知机模型的假设是定义在特征空间中的所有线性分类模型或者线性分类器$f\mid f(x)=(w\cdot x+b)$ 。在线性方程$w\cdot x+b=0$对应于问题空间中的一个超平面S(超平面的知识可以参考我的上一篇博客)，这个超平面将特征空间分为两个部分，如下图所示。oo作为一类，xx作为另一类，它们的特征很简单，就是它们的坐标。

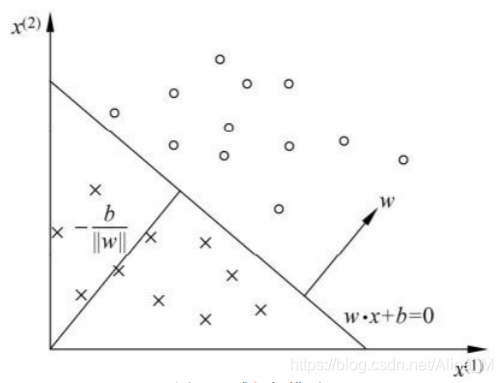
作为监督学习的中的一种二分类方法，感知机学习通过训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\} T={(x1​,y1​),(x2​,y2​),...,(xn​,yn​)}求得模型参数 $w,b$。感知机预测，通过学习得到的感知机模型，对于新输入的实例给出其对应的输出类别。

2.感知机学习策略

2.1 数据集的线性可分性

  任意的数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\} T={(x1​,y1​),(x2​,y2​),...,(xn​,yn​)}，其中$x\in \mathrm{X}=R^n$， y i ∈ Y = { + 1 , − 1 } y_i\in Y=\{+1,-1\} yi​∈Y={+1,−1}，如果存在某个超平面$S$能够将数据集的正实例和负实例完全正确的划分道超平面的两侧，则说明数据集$T$是线性可分数据集，否则，称数据集$T$线性不可分。

2.2 感知机学习策略

  如果训练的数据集是线性可分的，感知机学习的目的是学习一个可以将训练集划分为两部分的分离超平面，如何确定这个超平面就是确定这个超平面的模型参数$w，b$。如何求得模型参数，就需要有一个学习的策略，即定义一个损失函数，并且将损失函数极小化。
  在感知机中，我们选择误分类的样本点到超平面S的总距离为损失函数，则输入空间中任意一点$x_0$到超平面的距离可以表示为：

$$\frac{1}{\mid \mid w\mid \mid }\mid w\cdot x+b\mid \text{\hspace{1em}(3)}$$

公式(3)中的$\mid \mid w\mid \mid$为$L_2$范数，又称为$L_2$正则化。
然后，对于误分类的数据$(x_i,y_i)$来说，$-y_i(w\cdot x_i+b)>0$成立。因为当 $w\cdot x_i+b>0$时，$y_i=-1$，而当$w\cdot x_i+b<0$时，$y_i=+1$。所以，误分类的点$x_i$到超平面$S$的距离为：
$$-\frac{1}{\mid \mid w\mid \mid }{y}_i(w\cdot x_i+b)\text{\hspace{1em}(4)}$$
  通过上式可知，假设超平面$S$的误分类点集合为$M$，那么所有误分类点到超平面S的总距离为:
$$-\frac{1}{\mid \mid w\mid \mid }\sum _{x_i\in M}{y}_i(w\cdot x_i+b)\text{\hspace{1em}(5)}$$
如果不考虑$\frac{1}{\mid \mid w\mid \mid }$,则公式(5)就是感知机学习的 损失函数。
  给定训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\} T={(x1​,y1​),(x2​,y2​),...,(xn​,yn​)}，其中$x\in \mathrm{X}=R^n$， y i ∈ Y = { + 1 , − 1 } y_i\in Y=\{+1,-1\} yi​∈Y={+1,−1}。感知机的$sign(w\cdot x+b)$学习的损失函数定义为：
$$L(w,b)=-\frac{1}{\mid \mid w\mid \mid }\sum _{x_i\in M}{y}_i(w\cdot x_i+b)\text{\hspace{1em}(6)}$$
其中$M$为误分类点的集合。通过公式(6)可知$L(w,b)$函数非负，如果没有误分类的点，则损失函数的值为0,同时误分类的点越少，误分类的点离超平面越近，损失函数的值就越小。其实就是说误分类的点是参数$w，b$的线性函数。因为损失函数是连续可导函数，则就可以通过梯度下降方法寻找最优值。

3.感知机学习算法

  通过上一节的学习，我们将感知机学习的问题转换为了求解损失函数的最优化问题，使用的方法就是梯度下降方法。

3.1 感知机学习原始方法

  求损失函数的最优解。就是参数$w，b$，使其为损失函数极小化问题的解。
$$minL(w,b)=-\frac{1}{\mid \mid w\mid \mid }\sum _{x_i\in M}{y}_i(w\cdot x_i+b)\text{\hspace{1em}(7)}$$
  感知机学习算法是误分类驱动的，具体采用随机梯度下降的方法。首先，任意选取一个超平面$w_0,b_0$，然后用梯度下降法不断的极小化损失函数，极小化的过程不是一次使$M$中所有的误分类的点的梯度下降，而是随机选取一个误分类的点使其梯度下降。
  假设误分类点的集合$M$是固定的，那么损失函数$L(w,b)$的梯度(分别对$w,b$求偏导)为：
$$\frac{\partial L}{\partial w}=-\sum _{x_i\in M}{y}_i{x}_i\text{\hspace{1em}(8)}$$
$$\frac{\partial L}{\partial b}=-\sum _{x_i\in M}{y}_i\text{\hspace{1em}(9)}$$
  随机选取一个误分类点$(x_i,y_i)$，对$w,b$进行更新：
$$w\leftarrow w+\eta y_i{x}_i\text{\hspace{1em}(10)}$$
$$b\leftarrow b+\eta y_i\text{\hspace{1em}(11)}$$
上式中的$\eta (0<\eta \le 1)$是学习率，通过不断迭代可以期待损失函数$L(w,b)$不断减小，直至为0。综上所述给出感知机学习算法的原始形式。

  算法解释：当一个实例点被误分类，即位于分离超平面的错误一侧时，则调整w,b的值，使分离超平面向该误分类点的一侧移动，以减少该误分类点与超平面 间的距离，直至超平面越过该误分类点使其被正确分类。
例题2.1

题解：初始取$w_0=0,b_0=0$,其他具体的解释在此不再啰嗦，请参考《统计学习方法》。下面用代码实现。

"""
《统计学习方法书中的例题》
例题2.1
如图所示的训练数据集，其正实例的点是x1(3,3),x2(4,3)。负实例点是x3(1,1)。用感知机学习算法的原始形式求感知机模型的f(x)=sign(wx+b).
这里,w=(w(1),w(2)),x=(x(1),x(2))。学习率α=1
"""
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


class MyPercptron:
    # 感知机类
    def __init__(self):
        """初始属性，就是变量"""
        self.w = None  # 参数初始的时候不知道是多少维，所以要根据数据集的维度确定，初始为None
        self.b = 0  # 偏置为常数，定义为0
        self.l_rate = 1  # 学习率为1
    def fit(self,X_train,y_train):
        """
        :param X_train: 训练样本
        :param y_train: 标签
        :return:
        """
        # 根据训练数据的维度初始化参数w。如x1=(3,3），则self.w=(0,0)
        # shape[0]是行维度，shape[1]是列维度
        self.w = np.zeros(X_train.shape[1])

        # 检测每一个点是否被正确分类
        i=0
        while i<X_train.shape[0]:
            x = X_train[i]
            y= y_train[i]
            # 如果y*(wx+b)<=0，则该点为误判点，跟新w,b
            if  y*(np.dot(self.w, x) + self.b) <= 0:
                self.w = self.w + self.l_rate * np.dot(y, x)
                self.b = self.b +self.l_rate * y
                # print(self.w,self.b)  #输出每一的跟新参数
                # 如果是误判点，从头进行判断。判断跟新后的超平面是否对这些点进行了真确的分类
                i=0
            else:
                i+=1


def draw(X,w,b):
    #生产分离超平面上的两点
    X_new=np.array([[0], [6]])
    y_predict=-b-(w[0]*X_new)/w[1]
    #绘制训练数据集的散点图
    plt.plot(X[:2,0],X[:2,1],"g*",label="1")
    plt.plot(X[2:,0], X[2:,0], "rx",label="-1")
    #绘制分离超平面
    plt.plot(X_new,y_predict,"b-")
    #设置两坐标轴起止值
    plt.axis([0,6,0,6])
    #设置坐标轴标签
    plt.xlabel('x1')
    plt.ylabel('x2')
    #显示图例
    plt.legend()
    #显示图像
    plt.show()


# 主函数
def main():
    # 构造训练数据 numpy array
    X_train = np.array([[3,3],[4,3],[1,1]])
    y_train = np.array([1,1,-1])
    # 构建感知机对象，对数据集基线训练
    percptron = MyPercptron()
    percptron.fit(X_train,y_train)

    # 打印出结果
    print("===============")
    print(percptron.w,percptron.b)
    # 结果绘制
    # draw(X_train,percptron.w,percptron.b)


if __name__ == '__main__':
    main()

3.2 算法的收敛性

  书中证明了Novikoff定理，证明过程书中有详细的过程，因为本人数学功底较差，整个证明过推了几遍才程勉强理解。在此就不再说明了，需要弄懂完整证明过程的同学可以参考其他博客。

3.2 感知机学习算法的对偶形式

  书中感知机的对偶形式的基本思想是，将$w$和$b$表示为实例$x_i$和标签$y_i$的线性组合的形式，通过求解其系数求得$w$和$b$。在算法2.1中可以假设初始值$w_0$和$b_0$都为0,对于误分类的点$(x_i,y_i)$通过：
$$w\leftarrow w+\eta y_i{x}_i\text{\hspace{1em}(10)}$$
$$b\leftarrow b+\eta y_i\text{\hspace{1em}(11)}$$
不断的跟新$w,b$的值，设修改了$n$次，则$w,b$关于$(x_i,y_i)$的增量分别是${\alpha }_i{y}_i{x}_i$和${\alpha }_i{y}_i$，其中${\alpha }_i=n_i\eta$,然后，通过学习的过程可以看出，最后学习到的$w,b$可以分别表示为如下所示：
$$w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i\text{\hspace{1em}(12)}$$
$$b=\sum _{i=1}^N{\alpha }_i{y}_i\text{\hspace{1em}(13)}$$
这里的${\alpha }_i\ge 0$，当$\eta =1$时，表示第$i$个实例点由于误分类而进行更新的次数，实例点跟新的次数越多，意味着他离超平面$S$越近，也就是那正确的区分。
下面是感知机对偶形式的学习算法

由于训练实例仅以内积的形式出现，为方便，可预先将训练集中实例间的内积计算出来并以矩阵形式存储，这就是所谓的Gram矩阵。这可以方便计算。

例题2.2

求解：通过对偶形式求解。

"""
《统计学习方法书中的例题》
例题2.2
如图所示的训练数据集，其正实例的点是x1(3,3),x2(4,3)。负实例点是x3(1,1)。用感知机学习算法的对偶形式求感知机模型的f(x)=sign(wx+b).
这里,w=(w(1),w(2)),x=(x(1),x(2))。学习率α=1
"""

import numpy as np
import matplotlib.pyplot as plt


class Percetron:
    """
    感知机对偶形式实现
    """

    def __init__(self):
        """
        定义参数
        """
        self.a = None
        self.b = 0
        self.l_rate = 1
        self.w = None

    def Gram(self, X):
        """
        :param X: 训练样本
        :return:
        求解Gram矩阵
        """
        n_sample = X.shape[0]  # Gram矩阵的行列数值一样
        self.gram = np.zeros((n_sample, n_sample))  # Gram矩阵的大小维度N*N
        # 计算Gram矩阵
        # for i in range(n_sample):
        #     for j in range(n_sample):
        #         self.gram[i][j] = np.sum(X[i] * X[j])
        self.gram = np.dot(X,X.T)


    def jude(self, X, Y, index):
        """
        :param X:
        :param Y:
        :param index:
        :return:
        判定条件 yi(aj*yj*xj*xi+b)<=0
        """
        temp = self.b
        n_sample = X.shape[0]
        for j in range(n_sample):
            temp += self.a[j] * Y[j] * self.gram[index][j]
        return temp * Y[index]

    def fit(self, X, Y):
        """
        :param X:
        :param Y:
        :return:
        训练感知机模型
        """
        n_samples = X.shape[0]
        n_features = X.shape[1]
        self.a, self.b = [0] * n_samples, 0
        self.w = np.zeros(n_features)

        self.Gram(X)
        
        i = 0
        while i < n_samples:
            if self.jude(X, Y, i) <= 0:
                self.a[i] = self.a[i] + self.l_rate
                self.b = self.b + self.l_rate * Y[i]
                i = 0
            else:
                i += 1

        for j in range(n_samples):
            self.w += self.a[j] * X[j] * Y[j]
        return self


def draw(X, w, b):
    # 生产分离超平面上的两点
    X_new = np.array([[0], [6]])
    y_predict = -b - (w[0] * X_new) / w[1]
    # 绘制训练数据集的散点图
    plt.plot(X[:2, 0], X[:2, 1], "g*", label="1")
    plt.plot(X[2:, 0], X[2:, 0], "rx", label="-1")
    # 绘制分离超平面
    plt.plot(X_new, y_predict, "b-")
    # 设置两坐标轴起止值
    plt.axis([0, 6, 0, 6])
    # 设置坐标轴标签
    plt.xlabel('x1')
    plt.ylabel('x2')
    # 显示图例
    plt.legend()
    # 显示图像
    plt.show()


def main():
    # 数据集
    X = np.array([[3, 3], [3, 4], [1, 1]])
    Y = np.array([1, 1, -1])
    percetron = Percetron()
    percetron.fit(X, Y)
    print(percetron.w, percetron.b)
    draw(X, percetron.w, percetron.b)


if __name__ == '__main__':
    main()

问题1：感知机模型的假设空间是什么？模型的复杂度体现在哪里？
感知机模型的假设空间是分类超平面 $w\cdot x+b=0$
模型的复杂度主要体现在特征向量上，如果维度越大，模型就越复杂。
问题2：原始算法和对偶算法的复杂的对比？
原始算法，样本维度越大，复杂度越大
对偶算法，样本数量越大，复杂度越大

正则化知识补充

  正则化（Regularization）是机器学习中一种常用的技术，其主要目的是控制模型复杂度，减小过拟合。最基本的正则化方法是在原损失函数中添加惩罚项，对复杂度高的模型进行“惩罚”。其数学表达形式为：
$$\overline{L}(w;X;y)=L(w;X;y)+\alpha \Omega (w)\text{\hspace{1em}(补1)}$$
其中$X，y$为训练样本和对应的标签，$w$为权重系数，$L()$为损失函数，$\Omega (w)$
为惩罚项，可以理解为模型“规模”的某种度量。参数 $\alpha$控制正则化的强弱，不同的$\Omega$函数对权重$w$的最优解有不同的偏好，因此会产生不同的正则化效果，最常用的$\Omega$有两种，即$L_1$范数和$L_2$范数。相应称之为$L_1$ 正则化和$L_2$正则化。此时有：
$$L_1:\Omega (w)=\mid \mid W\mid {\mid }_1=\sum _{1=1}^n\mid w_i\mid \text{\hspace{1em}(补2)}$$
$$L_2:\Omega (w)=\mid \mid W\mid {\mid }_2^2=\sum _{1=1}^n{w}_i^2\text{\hspace{1em}(补3)}$$

$L_1$和$L_2$正则化推导

  模型的复杂程度可以用VC维来衡量。在统计学习理论中提供了量化模型的很多不同方法，其中VC维最有名，VC维度量二分类器的容量.VC维定义了该分类器能分类的训练样本的最大数目，例如假设存在$m$个不同$x$点的训练集，分类器可以任意的标记该$m$个不同的$x$点，VC维被定义为$m$的最大可能值。
  通常情况下，模型的VC维与系数$w$的个数成线性关系。系数$w$数量越多，VC维越大，模型就越复杂。因此，为了限制模型的复杂度，很自然的思路是减少系数 $w$ 的个数，即让 $w$向量中一些元素为0或者说限制 $w$ 中非零元素的个数。详细的推导过程可以参考：知乎

$L_1$和$L_2$正则化的理解、

• 基于约束条件最优化

  $L_1$ 正则化等价于在原优化目标函数中增加约束条件：$\mid \mid W\mid {\mid }_1\le C$
  $L_2$ 正则化等价于在原优化目标函数中增加约束条件：$\mid \mid W\mid {\mid }_2^2\le C$

• 基于最大后验概率估计

  $L_1$ 正则化可通过假设权重 $w$ 的先验分布为拉普拉斯分布，由最大后验概率估计导出。
  $L_2$ 正则化可通过假设权重 $w$ 的先验分布为高斯分布，由最大后验概率估计导出。

4 总结

  《统计学习方法中》的第一个算是写完了，基本是跟着书本来的，很多和书中的内容一样。也欢迎各位大佬指正。

5 参考

https://www.zhihu.com/question/26526858
https://zhuanlan.zhihu.com/p/29360425
https://zhuanlan.zhihu.com/p/59181670
https://blog.youkuaiyun.com/Alina_M/article/details/107045773
https://bigquant.com/community/t/topic/126061
https://github.com/SmallVagetable/machine_learning_python/blob/master/perceptron/perceptron_dual.py