【计量经济学】【高教版】第二次作业

第二次作业：
教材：伍德里奇。计量经济学导论：现代观点（第五版）。

第三章习题：必做 1，2，5，6，11，选做13
第四章习题：必做2，3，4，5，8，选做9，10，11

第三章

1.多元线性回归模型的基本假设是什么？在证明最小二乘估计量的无偏性和有效性的过程中，哪些基本假设起了作用？

多元线性回归模型的基本假设： 在多元线性回归模型中，我们通常假设以下条件成立： 线性关系：自变量和因变量之间存在线性关系；
多元正态性：误差项 $ϵ$ 服从均值为零、方差为常数 ${\sigma }^2$ 的多元正态分布；
没有多重共线性：自变量之间不存在高度相关的情况； 同方差性：误差项 $ϵ$ 的方差在不同自变量的取值范围内保持恒定；
独立性：误差项 $ϵ$ 是独立的，即不受其他误差项的影响。
在证明最小二乘估计量的无偏性和有效性的过程中，主要起作用的假设是多元正态性和同方差性。其中，多元正态性假设使得最小二乘估计量服从正态分布，从而能够进行假设检验和置信区间估计；同方差性假设则使得最小二乘估计量具有最小方差的性质，从而具有较好的精确性和可靠性。此外，若多重共线性存在，则最小二乘估计量可能会偏离真实值，失去无偏性和有效性。因此，多重共线性的检验和处理也是建立可靠多元线性回归模型的重要步骤。

2.在多元线性回归分析中，t检验与F检验有何不同？在一元线性回归分析中，二者是否有等价的作用？

t检验与F检验在多元线性回归分析中的不同：
t检验通常用于检验单个自变量对因变量的显著性，它计算了该自变量系数与标准误的比值，从而判断该系数是否显著不为零；
F检验通常用于检验所有自变量对因变量的联合显著性，它计算了回归平方和与残差平方和的比值，从而判断所有自变量的联合效应是否显著不为零。
在一元线性回归分析中，t检验与F检验有等价的作用：
当只有一个自变量时，t检验与F检验的结果是等价的。此时，t检验可以用于检验单个自变量对因变量的显著性，F检验可以用于检验回归模型的整体显著性，这两种方法得到的结果应该是一致的；
具体而言，当只有一个自变量时，F检验的计算公式等价于对该自变量的t检验的平方，即$F=t^2$。
总之，t检验和F检验在多元线性回归分析中有不同的作用，但在一元线性回归分析中，它们有等价的作用。

5.考虑下列两个模型：

1. $Y_i={\alpha }_0+{\alpha }_1{X}_{i1}+{\alpha }_2{X}_{i2}+u_i$
2. $Y_i-X_{i1}={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+v_i$

(1)证明：$\widehat{{\beta }_1}={\hat{\alpha }}_1-1,\widehat{{\beta }_0}={\hat{\alpha }}_0,\widehat{{\beta }_2}={\hat{\alpha }}_2$.
(2)证明：两个模型的最小二乘残差相等，即对任何$i$，有$\widehat{u_i}={\hat{v}}_i$
(3)在什么条件下，模型2的$R^2$小于模型1的$R^2$?

(1) 首先，将模型2转化为标准形式：$Y_i={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+(v_i+X_{i1})$。
然后，将模型1和模型2的误差平方和分别表示为：

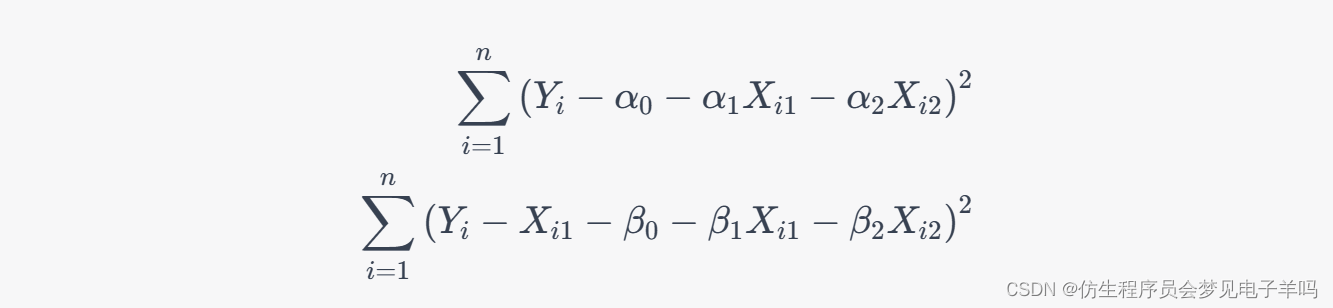
为了证明$\widehat{{\beta }_1}={\hat{\alpha }}_1-1,\widehat{{\beta }_0}={\hat{\alpha }}_0,\widehat{{\beta }_2}={\hat{\alpha }}_2$，我们只需要将模型2的误差平方和中的第二个括号展开，然后将模型1和模型2的误差平方和分别代入，得到：

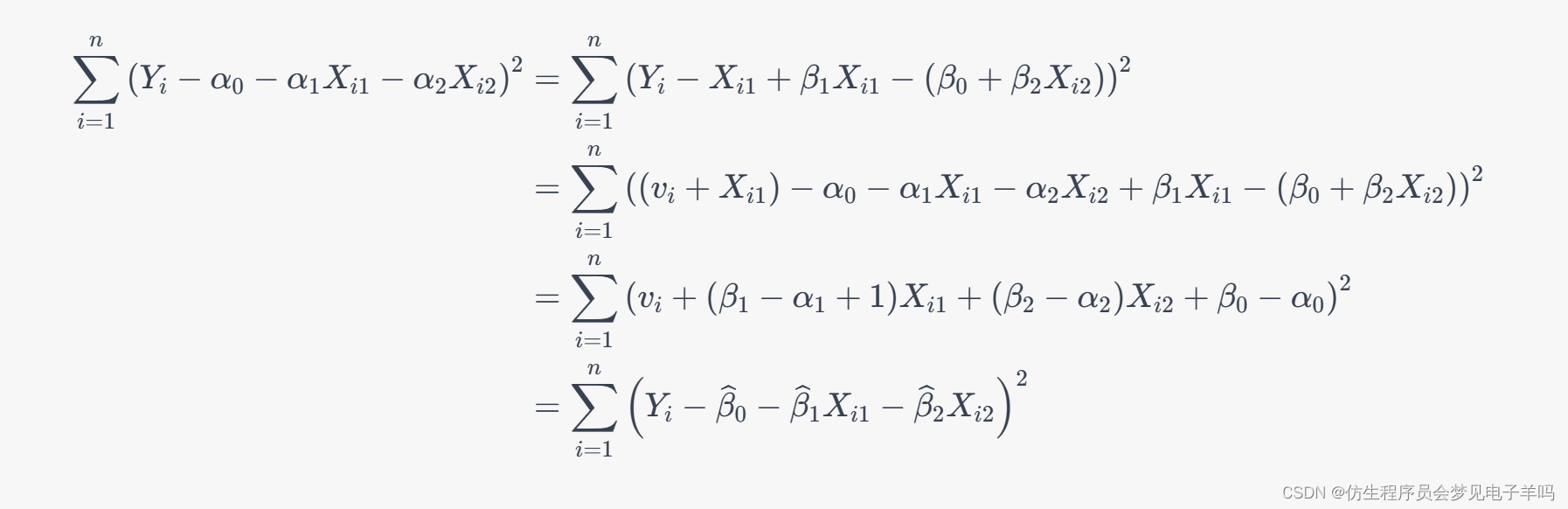
因此，我们可以得到$\widehat{{\beta }_1}={\hat{\alpha }}_1-1,\widehat{{\beta }_0}={\hat{\alpha }}_0,\widehat{{\beta }_2}={\hat{\alpha }}_2$。

(2) 为了证明两个模型的最小二乘残差相等，即对任何$i$，有$\widehat{u_i}={\hat{v}}_i$，我们只需要将模型2的误差平方和中的第二个括号展开，然后将模型1和模型2的误差平方和分别代入，得到：

6.考虑下列三个实验步骤：

6.考虑下列三个实验步骤：
（1）对$Y_i={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+u_i$进行回归；
（2）对$X_i={\alpha }_0+{\alpha }_1{X}_{i2}+v_i$进行回归,计算残差${\hat{v}}_i$；

（3）对$Y_i={\gamma }_0+{\gamma }_1\widehat{v_i}+{\gamma }_2{X}_{i2}+w_i$进行回归。
试证明$\widehat{{\beta }_1}=\widehat{{\gamma }_1}$，并直观地解释该结果。

首先，我们可以将第一个回归方程重写为 $Y_i={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+{ϵ}_i$，其中 ${ϵ}_i$ 是误差项，因为这个方程与第一个步骤等价。然后，我们可以将 $\hat{v}i$ 插入到第一个方程中，得到 $Y_i={\beta }_0+{\beta }_{1}Xi1+{\beta }_2{X}_{i2}+{\alpha }_0+{\alpha }_1{X}_{i2}+\hat{v}i+{ϵ}_i$。将其简化为 $Y_i=({\beta }_0+{\alpha }_0)+({\beta }_1+{\alpha }_1)Xi2+{\beta }_2{X}_{i2}+{\hat{v}}_i+{ϵ}_i$。

接下来，我们将第三个方程重写为 $Y_i={\gamma }_0+{\gamma }_1\widehat{v_i}+{\gamma }_2{X}_{i2}+{\eta }_i$，其中 ${\eta }_i$ 是误差项。然后我们可以将 $\hat{v}i$ 替换为第二步中计算的残差 $\hat{v}i=X_i-\widehat{{\alpha }_0}-\widehat{{\alpha }_1}Xi2$，得到 $Y_i={\gamma }_0+{\gamma }_1(X_i-\widehat{{\alpha }_0}-\widehat{{\alpha }_1}Xi2)+{\gamma }_2{X}_{i2}+{\eta }_i$。将其简化为 $Y_i={\gamma }_0-{\gamma }_1\widehat{{\alpha }_0}+({\gamma }_1-{\gamma }_2\widehat{{\alpha }_1})X_{i2}+{\gamma }_1{X}_i-{\gamma }_2{X}_{i2}^2+{\eta }_i$。

现在我们可以比较两个方程中的 $X_{i2}$ 的系数。我们注意到，$({\beta }_1+{\alpha }_1)$ 在第一个方程中是 $X_{i2}$ 的系数，而 $({\gamma }_1-{\gamma }_2\widehat{{\alpha }_1})$ 在第二个方程中是 $X_{i2}$ 的系数。因此，如果我们证明 $\widehat{{\beta }_1}={\beta }_1+{\alpha }_1$ 和 $\widehat{{\gamma }_1}={\gamma }_1-{\gamma }_2\widehat{{\alpha }_1}$，那么我们就证明了 $\widehat{{\beta }_1}=\widehat{{\gamma }_1}$。

我们知道，在第一个步骤中，$\widehat{{\beta }_1}=\frac{{\sum }_{i=1}^n(X_{i1}-\overline{X_1})(Y_i-\bar{Y})}{{\sum }_{i=1}^n(X_{i1}-\overline{X_1}{)}^2}$，这是 $X_{i1}$ 对 $Y_i$ 的回归系数的最小二乘估计量。因此，我们可以将
$\widehat{{\beta }_1}$ 展开为 $\widehat{{\beta }_1}=\frac{{\sum }_{i=1}^n{X}_{i1}{Y}_i-\overline{X_1}{\sum }_{i=1}^n{Y}_i}{{\sum }_{i=1}^n{X}_{i1}^2-n{\overline{X_1}}^2}$。然后，我们将 $X_i$ 插入到这个方程中，得到 $\widehat{{\beta }_1}=\frac{{\sum }_{i=1}^n(X_{i1}-\overline{X_1})({\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+{ϵ}_i)-\overline{X_1}{\sum }_{i=1}^n({\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+{ϵ}_i)}{{\sum }_{i=1}^n(X_{i1}-\overline{X_1}{)}^2-n{\overline{X_1}}^2}$。然后，我们可以将 ${ϵ}_i$ 替换为 $Y_i-{\beta }_0-{\beta }_1{X}_{i1}-{\beta }_2{X}_{i2}$，得到

其中，$\widehat{\mathrm{Cov}}(X_{i1},Y_i)$ 和 $\widehat{\mathrm{Var}}(X_{i1})$ 分别是 $X_{i1}$ 和 $Y_i$ 的样本协方差和样本方差的最小二乘估计量。
接下来，我们考虑第二个步骤。在第二个步骤中，我们对 $X_i$ 进行回归，得到 ${\hat{X}}_i=\widehat{{\alpha }_0}+\widehat{{\alpha }_1}{X}_{i2}$，其中 $\widehat{{\alpha }_0}$ 和 $\widehat{{\alpha }_1}$ 分别是 ${\alpha }_0$ 和 ${\alpha }_1$ 的

继续上面的回答，我们现在来考虑第三个步骤。在第三个步骤中，我们对 $Y_i$ 进行回归，得到

$$Y_i={\gamma }_0+{\gamma }_1\hat{v}i+{\gamma }_{2}Xi2+w_i.$$

我们可以将 $\hat{v}i$ 替换为 $X_i-\widehat{{\alpha }_0}-\widehat{{\alpha }_1}Xi2$，得到

$$Y_i={\gamma }_0+{\gamma }_1(X_i-\widehat{{\alpha }_0}-\widehat{{\alpha }_1}{X}_{i2})+{\gamma }_2{X}_{i2}+w_i.$$

展开后可得

$$Y_i=({\gamma }_0-{\gamma }_1\widehat{{\alpha }_0})+({\gamma }_1-{\gamma }_2\widehat{{\alpha }_1})X_i+({\gamma }_2)X_{i2}+w_i-{\gamma }_1{X}_{i2}\widehat{{\alpha }_1}.$$

我们可以将该方程与第一步骤中的回归方程进行比较，可以看到

11.下表给出三变量模型

11.下表给出三变量模型$Y_i={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+u_i$的回归结果：

方差来源	平方和（SS）	自由度（d.f.）	平方和的均值（MSS）
来自回归	65965	——	——
来自残差	——	——	——
总离差	66042	14

（1）求样本容量n、残差平方和RSS、回归平方和ESS以及残差平方和RSS的自由度。
（2）求拟合优度$R^2$及调整的拟合优度$\overline{R^2}$。
（3）检验假设：X1和X2对Y无影响。 应采用什么假设检验？为什么？
（4）根据以上信息，你能否确定X1和X2各自对Y的影响吗？

(1) 样本容量$n$为14，总离差平方和$TSS=66042$，回归平方和$ESS=65965$，因此残差平方和$RSS=TSS-ESS=77$。由于模型有两个自变量，所以回归的自由度为2，残差的自由度为$n-3=11$。

(2) 拟合优度$R^2=\frac{ESS}{TSS}=0.9978$，调整的拟合优度$\overline{R^2}=1-\frac{RSS/(n-3)}{TSS/(n-1)}=0.9962$。

(3) 可以采用F检验来检验假设$H_0:{\beta }_1={\beta }_2=0$，即X1和X2对Y无影响。在本例中，回归平方和$ESS=65965$，回归自由度为2，残差平方和$RSS=77$，残差自由度为11。因此，F统计量为

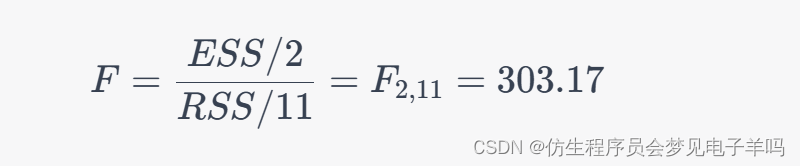
对于$H_0$，F统计量的p值极小，因此可以拒绝$H_0$，认为X1和X2对Y有影响。

(4) 由于该回归模型中有两个自变量，而只给出了总平方和、回归平方和和残差平方和的信息，无法准确确定X1和X2各自对Y的影响。需要进一步分析模型参数估计的显著性或进行模型诊断。

13.在考察两组回归函数是否有差异的F检验中，试证明：$RS{S}_U=RS{S}_1+RS{S}_2$
其中，$RS{S}_1$,$RS{S}_2$分别为两组对应各自样本下回归的残差平方和，$RS{S}_U$为两组对应样本合成的大样本下的回归的残差平方和。

设两组样本分别为样本1和样本2，样本1的回归模型为$Y_{1i}={\beta }_{10}+{\beta }_{11}{X}_{1i}+u_{1i}$，样本2的回归模型为$Y_{2i}={\beta }_{20}+{\beta }_{21}{X}_{2i}+u_{2i}$，则样本1和样本2的合成样本为$Y_i=\{\begin{array}{llc}{Y}_{1i}& \text{i=1,2,...,n1}{Y}_{2i-n_1}& \text{i=n1+1,n1+2,...,n1+n2}\end{array}$，其中$n_1$和$n_2$分别为样本1和样本2的样本容量，n为合成样本的总样本容量。

合成样本下的回归模型为$Y_i={\beta }_0+{\beta }_1{X}_{1i}+{\beta }_2{X}_{2i}+u_i$，其中${\beta }_0=\{\begin{array}{llc}{\beta }_{10}& \text{i=1,2,...,n1}{\beta }_{20}& \text{i=n1+1,n1+2,...,n1+n2}\end{array}$，${\beta }_1={\beta }_{11}$，${\beta }_2={\beta }_{21}$。合成样本下的残差平方和为$RS{S}_U={\sum }_{i=1}^{n_1+n_2}(Y_i-{\hat{\beta }}_0-\hat{\beta }1X1i-\hat{\beta }2X2i{)}^2$，其中${\hat{\beta }}_0$、${\hat{\beta }}_1$、${\hat{\beta }}_2$分别为合成样本下的回归系数估计值。由于样本1和样本2分别进行回归分析得到的残差平方和分别为$RS{S}_1$和$RS{S}_2$，则总的残差平方和为$RSS=RS{S}_1+RS{S}_2$。

将合成样本下的回归模型中的${\beta }_0$、${\beta }_1$、${\beta }_2$代入到$RS{S}_U$中，得到：

第四章

必做2，3，4，5，8，选做9，10，11

2.对一元回归模型

2.对一元回归模型$Y_i={\beta }_0+{\beta }_1{X}_i+{\mu }_i$，如果已知$Var({\mu }_i)={\sigma }_i^2$，则可对原模型以权1/$\sigma$相乘后变成如下的二元模型：
$\frac{Y_i}{{\sigma }_i}={\beta }_0\frac{1}{{\sigma }_i}+{\beta }_1\frac{X_i}{{\sigma }_i}+\frac{{\mu }_i}{{\sigma }_i}$
对该模型进行普通最小二乘估计就是加权最小二乘法。
试证明该模型的随机干扰项是同方差的，并求出${\beta }_1$的上述加权最小二乘估计量。

3.试证明，二元线性回归模型…

4.在教材中已指出，对截面数据，

在教材中已指出，对截面数据，引起解释变量内生性的原因主要有三种情形，其中第三种情形是解释变量存在着测量误差。对于一元回归模型$Y_i={\beta }_0+{\beta }_1{X}_i^{\ast }+{\mu }_i$,假设解释变量$X_i^{\ast }$的实测值$X_i$与之有偏误：$X_i=X_i^{\ast }-e_i$，其中$e_i$是具有零均值且与$X_i^{\ast }$及${\mu }_i$不相关的随机变量。
试问能否将$X_i=X_i^{\ast }-e_i$代入原模型，使之变换成$Y_i={\beta }_0+{\beta }_1{X}_i+v_i$后进行估计？其中，$v_i$为变换后模型的随机干扰项。

5试证明两式等价

试证明$\frac{1}{n}\Sigma Z_i^{{}^{\prime }}(Y_i-X_i\tilde{\beta })=0$与式$\frac{1}{n}\Sigma Z^{{}^{\prime }}(Y-X\tilde{\beta })=0$是等价的。

8如果X1和X2在给定的样本下不相关

如果X1和X2在给定的样本下不相关（正交），则通过教材式（4.4.7）证明：${\alpha }_1$的估计满足无偏性与一致性，但${\alpha }_0$的估计却是有偏且非一致的。

9记教材中正确设定的模型

记教材中正确设定的模型（4.4.1）$Y={\beta }_o+{\beta }_1{X}_1+{\beta }_2{X}_2+\mu$的随机干扰项的方差为${\sigma }_{\mu }^2$，非正确设定的模型（4.4.2）$Y={\alpha }_0+{\alpha }_1{X}_1+v$的随机干扰项的方差为${\sigma }_v^2$，试证明${\sigma }_{\mu }^2⩽{\sigma }_v^2$。

10却拟合了一个带截距项的模型

如果真实的模型是$Y_i={\beta }_1{X}_i+{\mu }_i$，但你却拟合了一个带截距项的模型$Y_i={\alpha }_0+{\alpha }_1{X}_i+v_i$ ，试评述这一设定误差的后果。

11 你却对过原点的模型进行了普通最小二乘回归

在习题10中，假设真实的模型是带截距项的模型，而你却对过原点的模型进行了普通最小二乘回归。请评述这一模型假设的后果。