算法与数据结构 树

1. 树的定义

• 树是由n （n >= 0）个结点所构成的有限集合
• 当 n = 0时，称为空树；
• 当n > 0时，n 个结点满足以下条件：
  （1）有且仅有一个称为根的结点；
  （2）其余结点可分为 m （m >= 0）个互不相交的有限集合，且每一个集合又构成一个树，这棵树称为根结点的子树。
  上述定义采用的是递归方式。事实上，树的层次结构体现了元素之间具有的层次关系，即对于一颗非空树，其中有且仅有一个没有前驱的结点，称为根结点。其余结点都有且仅有一个前驱，但是可以有多个后继。

2. 树的常用术语

• 树的结点：树的结点是由一个数据元素及关联其子树的边所组成。

• 结点的路径：结点的路径是指从根结点到该结点的所经历的结点和分支的顺序。

• 路径的长度：路径的长度是指结点路径中所包含的分支数。

• 结点的度：结点的度是指该结点所拥有子树的数目。

• 树的度：树的度是指树中所有结点的度的最大值。

• 叶结点（终端结点）：叶结点是指树中度为 0 的结点。

• 分支结点（非终端结点）：分支结点是指树中度不为 0 的结点。

• 孩子结点（子结点）：一个结点的孩子结点是指这个结点的子树的根结点。

• 双亲结点（父结点）：一个结点的双亲结点是指若树中某个结点有孩子结点，则该结点称为孩子结点的双亲结点。
  双亲结点和孩子结点也称为具有互为前驱和后继关系的结点，其中，双亲结点是孩子结点的前驱，而孩子结点是双亲结点的后继。

• 子孙结点：一个结点的子孙结点是指这个结点的所有子树中任意结点。

• 祖先结点：一个结点的祖先结点是指该结点的路径中除此结点之外的所有结点。

• 兄弟结点：兄弟结点是指具有同一双亲的结点。

• 结点的层次：规定树中根结点的层次为 0 ，则其他结点的层次是其双亲结点的层次数加 1 。

• 树的深度：树的深度是指树中所有结点的层次数的最大值加 1 。

• 有序树：有序树是指树中各结点的所有子树之间从左至右有严格的次序关系，不能互换位置。也就是说如果子树的顺序不同则对应着不同的有序树。如下图
  

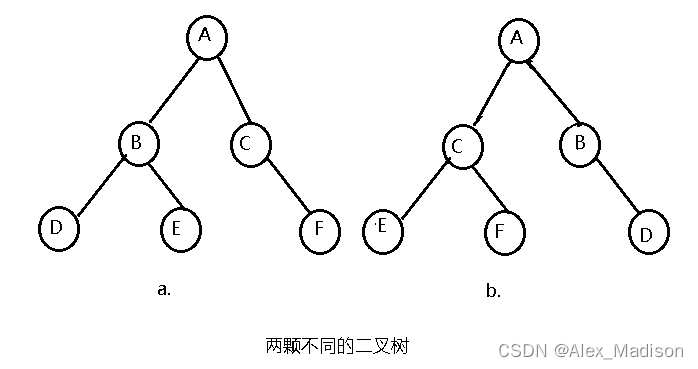
• 无序树：与有序树相反，无序树是指树中各结点的所有子树之间没有严格的次序之分，其次序可以任意更换。

• 森林：森林是指由（m >= 0）棵互不相交的树构成的集合。