机器学习：聚类

聚类是机器学习中的一种无监督学习方法，它旨在将数据集中的样本分成相似的组别或簇，使得同一组内的样本相互之间更为相似，而不同组之间的样本差异较大。以下是聚类的一些关键概念和方法：

1.K均值聚类（K-Means Clustering）：

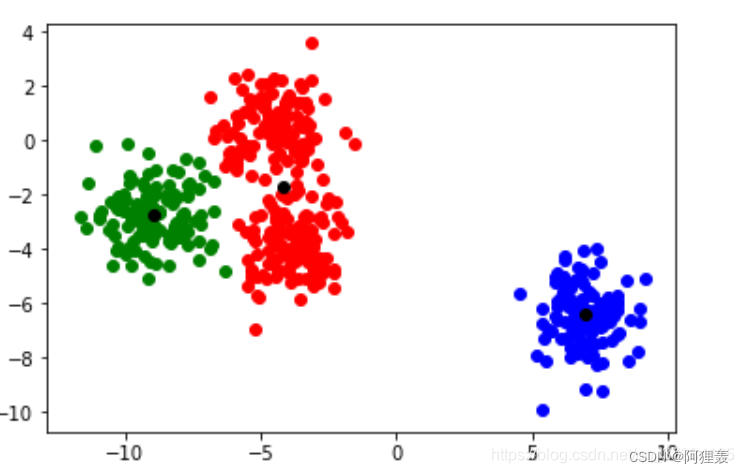
K均值聚类（K-Means Clustering）是一种常见的无监督学习算法，用于将数据集中的样本划分成K个簇。这里简要介绍K均值聚类的基本原理和步骤：

• 初始化： 选择K个初始中心点，通常从数据集中随机选择。这些中心点将作为簇的代表。

• 分配数据点： 对数据集中的每个样本，将其分配给距离最近的中心点所对应的簇。这一步使用欧氏距离或其他距离度量。

• 更新簇中心： 对每个簇，计算其所有成员样本的均值，将均值作为新的簇中心。

• 重复迭代： 重复步骤2和步骤3，直到簇中心不再发生显著变化或达到预定的迭代次数。

• 输出结果： 最终得到K个簇，每个簇包含一组相似的数据点。

K均值聚类的优点包括简单易实现、计算效率高，尤其对于大规模数据集较为适用。然而，它也有一些缺点，如对初始中心点的敏感性、对异常值的敏感性，以及对非球形簇结构的适应性较差。

在实际应用中，为了避免局部最优解，常常运行算法多次并选择最好的结果。同时，选择合适的簇数K也是关键，可以通过Elbow方法等方式进行估计。

2.层次聚类（Hierarchical Clustering）：

层次聚类（Hierarchical Clustering）是一种无监督学习方法，它以树状结构（树状图或树状图谱）表示数据集中样本的聚类关系。层次聚类可以分为两种主要方法：凝聚层次聚类和分裂层次聚类。

• 凝聚层次聚类（Agglomerative Hierarchical Clustering）：

  • 初始状态： 将每个数据点视为一个单独的簇。
  • 合并过程： 通过迭代地合并最相似的簇，形成一个层次结构，直至所有数据点合并为一个大的簇。
  • 相似度度量： 通过定义不同的相似度度量（如欧氏距离、曼哈顿距离等），确定簇的相似性。

• 分裂层次聚类（Divisive Hierarchical Clustering）：

  • 初始状态： 将所有数据点视为一个大的簇。
  • 分裂过程： 通过迭代地将最不相似的簇分裂为较小的簇，形成一个层次结构，直至每个数据点都成为一个独立的簇。
  • 相似度度量： 同样使用不同的相似度度量确定簇的相似性。

在层次聚类的结果中，树状结构的每个节点代表一个簇，叶子节点表示单个数据点。这种层次结构可以通过树状图直观地展示不同层次的聚类结果。

层次聚类的优点包括不需要预先指定簇的数量、结果的可视化直观，但缺点包括计算复杂度较高，特别是对于大型数据集。在选择相似度度量和连接方式（单链接、全链接等）时，需要根据具体问题和数据特征进行调整。

3.DBSCAN（Density-Based Spatial Clustering of Applications with Noise）：

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种密度聚类算法，它能够发现任意形状的簇，并在聚类的同时识别噪声点。以下是DBSCAN的基本原理和步骤：

• 核心对象（Core Points）： 对于每个数据点，以指定的半径（ε，epsilon）内的邻域内的数据点数量（包括自身），如果这个数量大于等于一个预定的阈值（MinPts），则该点被认为是核心对象。

• 密度可达（Density-Reachable）： 如果一个点在另一个点的邻域内࿰