python学习一点 快乐一点（5）判断一组不等式是否满足约束并输出最大差

判断一组不等式是否满足约束并输出最大差

要求：1s 65535k

给定一组不等式，判断是否成立并输出不等式的最大差（输出浮点数的整数部分）
要求：
1>不等式系数为double类型，是一个二维数组
2>不等式的变量类型为int类型，是一维数组
3>不等式的目标值为double类型，是一维数组
4>不等式的约束为字符串数组，只能是：">",">=","=","<=","<"

输入描述：a11,a12,a13,a14,a15;a21,a22,a23,a24,a25;a31,a32,a33,a34,a35;*1,*2,*3,*4,*5;b1,b2,b3,b4,b5;<=,<=,<=
输出描述：
true或者false,最大差

#!/usr/bin/python
# -*- coding: utf-8 -*-
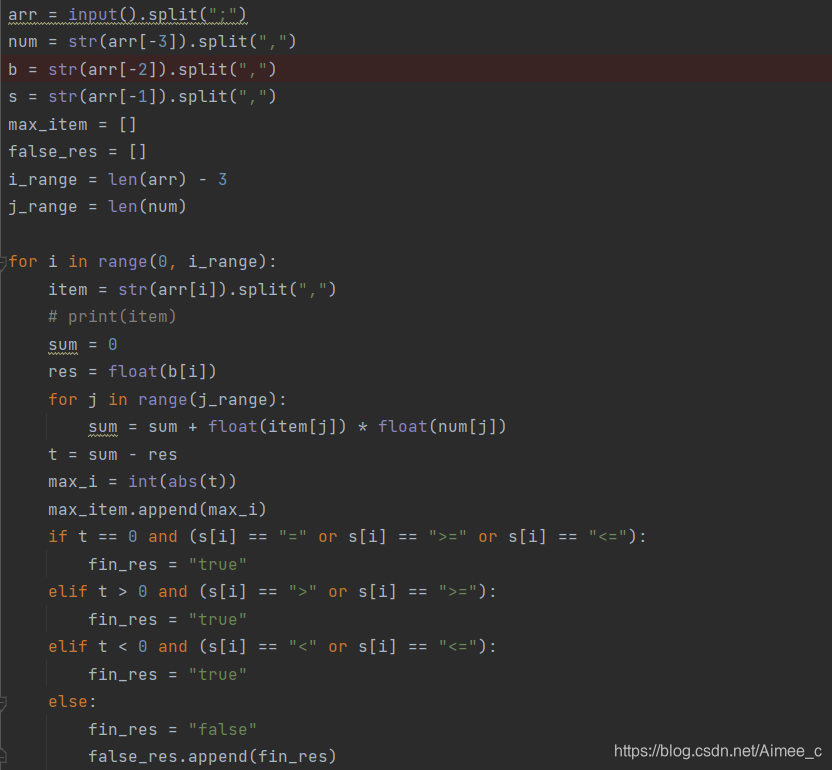
arr = input().split(";")
num=str(arr[-3]).split(",")
b=str(arr[-2]).split(",")
s=str(arr[-1]).split(",")
max_item = []
false_res = []
i_range = len(arr) - 3
j_range = len(num)

for i in range(0,i_range):
    item = str(arr[i]).split(",")
    # print(item)
    sum = 0
    res = float(b[i])
    for j in range(j_range):
        sum = sum + float(item[j])*float(num[j])
    t =sum-res
    max_i = int(abs(t))
    max_item.append(max_i)
    if t == 0 and (s[i]=="=" or s[i]==">=" or s[i]=="<="):
        fin_res="true"
    elif t > 0 and (s[i]==">" or s[i]==">=") :
        fin_res="true"
    elif t < 0 and (s[i]=="<" or s[i]=="<=") :
        fin_res="true"
    else:
        fin_res="false"
        false_res.append(fin_res)


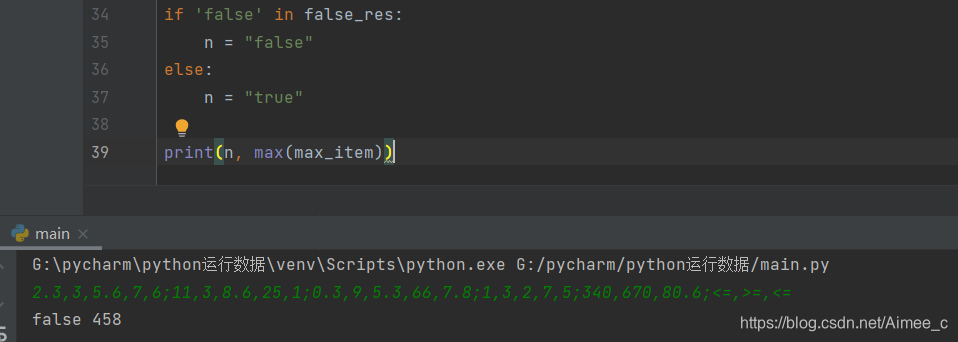
if 'false' in false_res:
    n = "false"
else:
    n = "true"
    
print(n,max(max_item))