一、人工智能研究的方法及途径
1. 符号主义学派(逻辑主义、心理学派、计算机学派) 主要观点:AI起源于数理逻辑,人类认知的基元是符号,认知过程是符 号表示上的一种运算 代表性成果:厄尔和西蒙等人研制的称为逻辑理论机的数学定理证明程 序LT 代表人物:纽厄尔、肖、西蒙和尼尔逊(Nilsson)等
符号主义 智能的基础是知识,其核心是知识表示和知识推理;知识可用符号表 示,也可用符号进行推理,因而可以建立基于知识的人类智能和机器智能 的统一的理论体系
2. 联结主义学派(仿生学派或生理学派) 主要观点:AI起源于仿生学,特别是人脑模型,人类认知的基元是神经 元,认知过程是神经元的联结活动过程 代表性成果:由麦克洛奇和皮兹创立的脑模型,即MP模型 代表人物:麦克洛奇和皮兹
联结主义 思维的基元是神经元,而不是符号;思维过程是神经元的联结活动过 程,而不是符号运算过程;反对符号主义关于物理符号系统的假设。
3. 行为主义学派(进化主义、控制论学派) 主要观点:AI起源于控制论,智能取决于感知和行为,取决于对外界复 杂环境的适应,而不是推理。 代表性成果:布鲁克斯研制的机器虫 代表人物: 布鲁克斯
行为主义 智能取决于感知和行动,提出了智能行为的“感知—动作”模型;智 能不需要知识、不需要表示、不需要推理;人工智能可以像人类智能那样 逐步进化。
二、产生式系统
1.产生式系统的组成
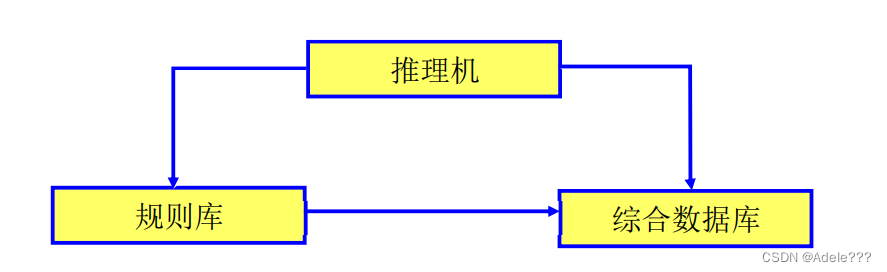
把一组产生式放在一起,让它们互相配合,协同作用, 一 个产生式的结论可以供给另个产生式作为前提使用,以这种 方式求得问题的解决,这样的系统称为产生式系统
规则库 用于描述某领域内知识的产生式集合,包含着将问题从初始状态转换成目标 状态(或解状态)的变换规则。是专家系统的核心。
综合数据库 又称为事实库,用于存放输入的初始事实、外部数据库输入的事实以及中间 结果(事实)和最后结果的工作区。 是动态的。
推理机 是一个或一组程序,用来控制和协调规则库与综合数据库的运行,包含了推 理方式、控制策略。 确定选用什么规则或如何应用规则
通常从选择规则到执行操作分3步完成:匹配、冲突解决和操作
匹配:匹配就是将当前综合数据库中的事实与规则中的条件进行比较, 如果相匹配,则这一规则称为匹配规则。
冲突解决:当有多条匹配规则时,通过冲突解决策略选中的在操作部 分执行的规则称为启用规则。冲突解决的策略有很多种 , 其中专一性 排序、规则排序、规模排序和就近排序是比较常见的冲突解决策略。
操作:操作就是执行规则的操作部分。经过操作以后,当前的综合数 据库将被修改,其他的规则有可能将成为启用规则。
三、最佳优先搜索
最佳优先搜索又称为有序搜索或择优搜索,OPEN表节点按估价函数f(x)的值排序, 选择函数值最小的节点作为下一个被考察的节点;最佳优先搜索又分 局部最佳优先搜索和全局最佳优先搜索。
局部最佳优先搜索 基本思想:当一个节点x被扩展以后,对每个子节点按f(x)的值排序, 并从新扩展的子节点中选择估计值最小的节点作为下一个考察对象。
全局最佳优先搜索基本思想:在OPEN表中的全部节点中选择一个估价函数值f(x)最小的 节点,作为下一个被考察的节点。因为选择的范围是OPEN表中的全部 节点,所以它称为全局最佳优先搜索或全局择优搜索
1.八数码问题
例:用全局最佳优先搜索方法求解八数码问题 S0 Sg 初始状态 目标状态
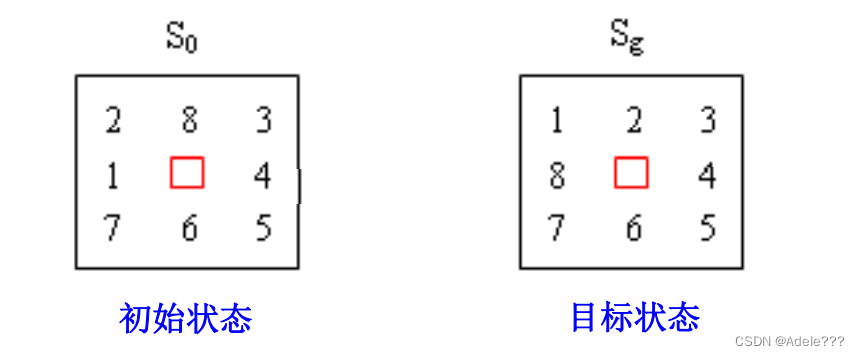
g(x):表示节点x的深度 h1 (x):表示节点x的格局与目标节点的格局错放的棋子个数
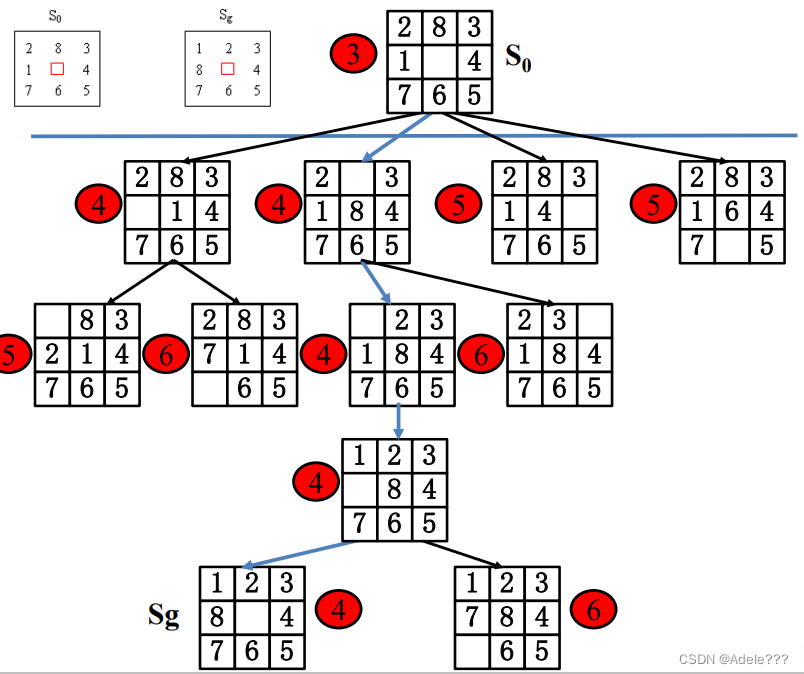
四、树的配置
解树的代价可按如下规则计算:
(1)若n为终止节点,则其代价h(n)=0;
(2)若n为或节点,且子节点为n1 , n2 , … ,nk,则n的代价为:
![]()
其中,c(n, ni )是节点n到其子节点ni的边代价。
(3)若n为与节点,且子节点为n1 , n2 , … ,nk,则n的代价可用和代价法或最大代价法 若用和代价法,则其计算公式为:
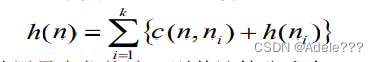
若用最大代价法,则其计算公式为:
![]()
(4)若n是端节点,但又不是终止节点,则n不可扩展,其代价定义为h(n)=∝ (5)根节点的代价即为解树的代价。
例题 :
例:设下图是一棵与/或树,它包括两棵解树,左边的解树由S0、A、 t1、C及t3组成;右边的解树由S0、B、t2、D及t4组成。在该树中,t1、 t2、t3、t4为终止节点;E、F是端节点;边上的数字是该边的代价。 请计算解树的代价。
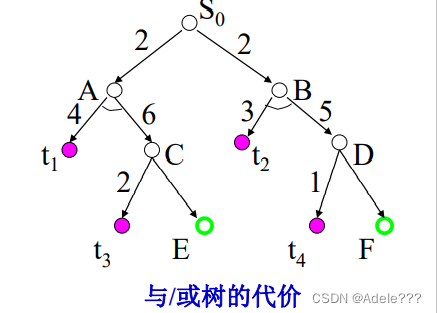
解:先计算左边的解树
按和代价:h(S0 )=2+4+6+2=14
按最大代价:h(S0 )=(2+6)+2=10
再计算右边的解树
按和代价:h(S0 )=1+5+3+2=11
按最大代价:h(S0 )=(1+5)+2=8
五、谓词公式的范式
前束型范式
一个谓词公式,如果它的所有量词均非否定地出现在公式的最前面,且 它的辖域一直延伸到公式之末,同时公式中不出现连接词→及 ,这 种形式的公式称作前束型范式。
例如,公式( x)(y)( z)(P(x)∧F(y,z)∧Q(y,z)),即是一个前束形的公式。
![]()
Skolem范式(斯克林范式)
从前束形范式中消去全部存在量词所得到的公式即为Skolem范式,或称 Skolem标准型。
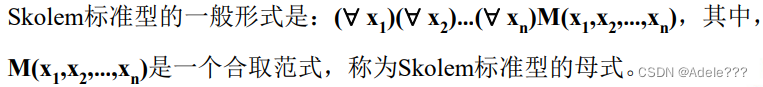
常用逻辑等价式和蕴含式


六、归结推理
归结演绎推理
鲁滨逊归结原理把永真性的证明转化为关于不可满足性的证明。
反证法:P ⇒ Q ,当且仅当 P∧~Q ⇔ F ,即 Q为 P 的逻辑结论,当 且仅当 P∧~Q 是不可满足的。
海伯伦(Herbrand)定理为自动定理证明奠定了理论基础。
鲁滨逊(Robinson)提出的归结原理使机器定理证明成为现实。
不可满足意义下的一致性
定理:设有谓词公式G,而其相应的子句集为S,则G是不可满足的充分 必要条件是S是不可满足的。
强调:公式G与其子句集S并不等值,只是在不可满足意义下等价。 P=P1∧P2∧… ∧Pn的子句集
当P=P1∧P2∧… ∧Pn时,若设P的子句集为SP,Pi的子句集为Si,则一般情 况下,SP并不等于S1∪S2∪S3…∪Sn,而是要比S1∪S2∪S3…∪Sn复杂得多。 但是,在不可满足的意义下,子句集SP与S1∪S2∪S3…∪Sn是一致的,即: SP不可满足
S1∪S2∪S3…∪Sn不可满足
命题逻辑中的归结原理
归结与归结式:设C1与C2是子句集中的任意两个子句,如果C1中的文字 L1与C2中的文字L2互补,则从C1和C2中可以分别消去L1和L2,并将二子 句中余下的部分做析取构成一个新的子句C12,称这一过程为归结,所 得到的子句C12称为C1和C2的归结式,而称C1和C2为C12的亲本子句。
可以用下面的式子解释这个定义。设两个子句:
C1 =P∨C1 ′
C2 =~P∨C2 ′
P和~P是两个互补文字,则消去互补文字后得: C12 = C1 ′∨C2 ′
这一归结过程就是一种推理规则。归结推理方法就只有这么一条规则。
归结原理
归结式C12是其亲本子句C1和C2的逻辑结论。
设C1和C2是子句集S上的子句,C12是C1和C2的归结式。如果把C12加入 子句集S后得到新子句集S1,则S1和S在不可满足的意义下是等价的。即: S是不可满足的 S1是不可满足的。
归结推理过程: 子句集S不可满足性的推理过程如下:
(1) 对子句集S中的各子句间使用归结推理规则。
(2) 将归结所得的归结式放入子句集S中,得新子句集S′。
(3) 检查子句集S′中是否有空子句(NIL),若有则停止推理;否则转(4)。
(4) 置S=S′,转步骤(1)。
例如:设已知的公式集为: { P, (P∧Q)→R, (S∨T)→Q, T },求证结论R。 解:假设结论R为假, 将﹁R加入公式集,并 化为子句集: S={P,﹁P∨﹁Q∨R, ﹁S∨Q, ﹁T∨Q, T, ﹁R} 其归结过程如右图的归结演绎树所示。该树 根为空子句。 子句集S不可满足,即假设﹁R为真是错误的, 于是R为真。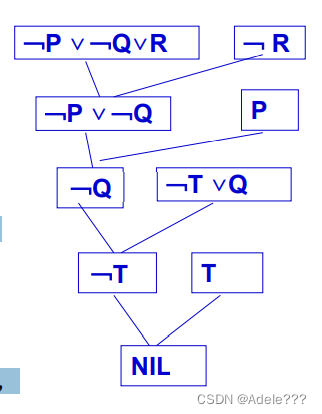

目录




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








