算法笔记习题 3-1小节~PAT

于 2019-03-08 20:20:34 发布
阅读量1k 收藏
点赞数
CC 4.0 BY-SA版权
分类专栏： 算法笔记 PAT 文章标签： 算法笔记 pAT
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/Ada_lake/article/details/88178840
本文详细解析PAT算法竞赛中的经典题目，涵盖卡拉兹猜想验证、挖掘机技能大赛评分、大整数运算等，通过实例代码展示算法设计与实现技巧。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

算法笔记@Ada_Lake

算法笔记代码保留地~~~

PAT上的习题

3.1小节——入门模拟->简单模拟

1001 害死人不偿命的(3n+1)猜想 （15 分）
  1. 题目描述 ，卡拉兹(Callatz)猜想：
    对任何一个正整数 n，如果它是偶数，那么把它砍掉一半；如果它是奇数，那么把 (3n+1) 砍掉一半。这样一直反复砍下去，最后一定在某一步得到 n=1。卡拉兹在 1950 年的世界数学家大会上公布了这个猜想，传说当时耶鲁大学师生齐动员，拼命想证明这个貌似很傻很天真的命题，结果闹得学生们无心学业，一心只证 (3n+1)，以至于有人说这是一个阴谋，卡拉兹是在蓄意延缓美国数学界教学与科研的进展……
    我们今天的题目不是证明卡拉兹猜想，而是对给定的任一不超过 1000 的正整数 n，简单地数一下，需要多少步（砍几下）才能得到 n=1？
  2. 输入格式：，每个测试输入包含 1 个测试用例，即给出正整数 n 的值
  3. 输出格式：，输出从 n 计算到 1 需要的步数。
  4. 样例输入,
    3
  5. 样例输出,
    5

我的理解
1.输出不要掉\n,否则PAT会检测为错误
2.我用的是c++编译器，因此将头文件改为了 #include

以下是代码

// Ada
#include<cstdio>

int main() {
	int n, flag = 0;
	scanf("%d", &n);
	while( (n != 1) &&(n <= 1000) ) {
		if(n % 2 == 0) {
			n /= 2;
		}
		else {
			n = ( 3 * n + 1 ) / 2;	
		}	
		flag++;
	}
	printf("%d\n", flag);
	
	
	return 0;
}
1032 挖掘机技术哪家强 （20 分）
  1. 题目描述 ，为了用事实说明挖掘机技术到底哪家强，PAT 组织了一场挖掘机技能大赛。现请你根据比赛结果统计出技术最强的那个学校。
  2. 输入，输入在第 1 行给出不超过 105
    的正整数 N，即参赛人数。随后 N 行，每行给出一位参赛者的信息和成绩，包括其所代表的学校的编号（从 1 开始连续编号）、及其比赛成绩（百分制），中间以空格分隔。
  3. 输出，在一行中给出总得分最高的学校的编号、及其总分，中间以空格分隔。题目保证答案唯一，没有并列。
  4. 样例输入,
    6
    3 65
    2 80
    1 100
    2 70
    3 40
    3 0
  5. 样例输出,
    2 150

我的理解
1.第一句话:给出的整数不超过105的参赛人数。即需要一个变量保存人数
2.有参赛者编号和成绩。 即有两个变量，一个存放参赛者编号，一个存放参赛者成绩
3.主要在于，要将同所学校的分数加起来。即如何看是不是同一个学校的。直接用一个数组存放参赛者的成绩。数组下标即为参赛者编号。当数组下标相同时，成绩就加起来
4.用一个变量表示总共有多少不同的学校
5.循环比较每一所学校的成绩，并最终输出最高值

**以下是代码**

// Ada
#include<cstdio>
const int maxn = 100010;
int school[maxn] = {0};
 
int main() {
	int n, schID, score; //参赛人数 
	scanf("%d", &n);
	for(int i = 0; i < n; i++){
		scanf("%d%d", &schID, &score);
		school[schID] += score;	
	}
	int k = 1, max = -1;
	for(int i = 1; i <= n; i++) {
		if(school[i] > max) {
			max = school[i];
			k = i;
		}
	}
	printf("%d %d", k, max); 
	
	return 0;
}

1.由题意第一句话，输入参赛人数 N 即scanf("%d", &N); 但人数不超过105
2.随后N行，每行给出一位参赛者的信息和成绩 即刚刚输入的N在这里被当作循环条件，输入两个整数，学校编号和比赛成绩。
3.要得到总得分最高的学校编号及总分，那么编号和总分就是一一对应的。并说明了学校编号从1开始连续编号，刚好数组可表示这种一一对应的关系，且下标是连续的数字。
即写出一个数组，初始值为零。下标范围刚好和前面的人数不超过105相对应。也就是说当所有人都来自不同学校的时候，取值最大。数字太大，用const常量简化表示 为什么这里是const int maxn = 100010 而不是 100000 ？？？谁能告诉我？？ - [x]
4.输入编号和成绩之后，恰好编号是数组下标，则下标相同的就可以相加得到同一下标的总分数。
5.现在比较最大值 将编号和最大值设一个初始值
// int k = 1, max = 0;
// k初始值只能是1，因为学校编号是从1开始连续编号。设为其他值没有意义。
// max值不可以是1，因为比赛成绩百分制， 有可能分数全为0，就是假分数了。
// 但我觉得。。。。。max是可以为0的，只能说设置为-1更有意义吧。。。

3.1小节——算法笔记上机训练实战指南

B001害死人不偿命的(3n+1)猜想 前方Get
1011 A+B 和 C （15 分）
  1. 题目描述 ，给定区间 [−2​31 ,2​31​​ ] 内的 3 个整数 A、B 和 C，请判断 A+B 是否大于 C。
  2. 输入格式：， 输入第 1 行给出正整数 T (≤10)，是测试用例的个数。随后给出 T 组测试用例，每组占一行，顺序给出 A、B 和 C。整数间以空格分隔。
  3. 输出格式：，对每组测试用例，在一行中输出 Case #X: true 如果 A+B>C，否则输出 Case #X: false，其中 X 是测试用例的编号（从 1 开始）。
  4. 样例输入,
    4
    1 2 3
    2 3 4
    2147483647 0 2147483646
    0 -2147483648 -2147483647
  5. 样例输出,
    Case #1: false
    Case #2: true
    Case #3: true
    Case #4: false

我的理解
1.给定区间 [−2​31 ,2​31​​ ] 内的 3 个整数 A、B 和 C。即输入三个数A, B，C。注意区间，要超出整型范围了
2.输入正整数T,是测试用例的个数，即是输入的循环条件
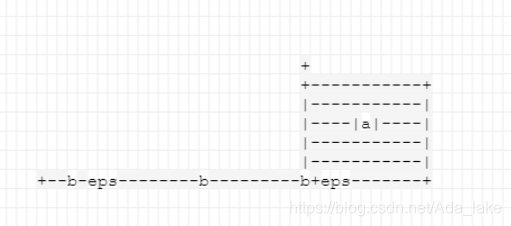
3.看A+B>C是否正确，用到了2.9的补充，浮点数的比较。大于是
#define More（a, b） (((a) - (b)) > (eps))
在这里插入图片描述

**以下是代码**

// Ada
#include<cstdio>

int main() {
	long long A, B, C;
	int T;
	scanf("%d", &T);
	for(int i = 1; i <= T; i++) {
		scanf("%lld %lld %lld", &A, &B, &C);
		if( A + B > C) {
			printf("Case #%d: true\n", i);
		}
		else {
			printf("Case #%d: false\n", i);
		}	
	}

	return 0;
}

弄错了

1.eps是浮点数 的比较，这里已经说明了是整数，直接比较
2.整型的范围在[−2​31 ,2​31​​-1 ]，这里的范围已经超过了整型的范围。并且相加范围会更有可能超出，因此这里应该使用long long

1016 部分A+B （15 分）
  1. 题目描述 ，正整数 A 的“D​A
    ​​ （为 1 位整数）部分”定义为由 A 中所有 D​A组成的新整数 P​A。例如：给定 A=3862767，D​A=6，则 A 的“6 部分”P​A是 66，因为 A 中有 2 个 6。现给定 A、D​A​​ 、B、D​B，请编写程序计算 P​A+P​B​​ 。
  2. 输入，输入在一行中依次给出 A、D​A、B、D​B，中间以空格分隔，其中 0<A,B<10​10。
  3. 输出，在一行中输出 P​A​​ + P​B的值。
  4. 输入样例 1：
    3862767 6 13530293 3
  5. 输出样例 1：
    399
  6. 输入样例 2：
    3862767 1 13530293 8
  7. 输出样例 2：
    0
    我的理解
    用数组或者直接数字相加。数字相加用枚举
    以下是代码
// Ada
#include<cstdio>

int main() {
	int p(char a[], int);
	char A[11], B[11];
	int C, D, SumA = 0, SumB = 0;
	
	scanf("%s %d %s %d", A, &C, B, &D);
	SumA = p(A, C);
	SumB = p(B, D);
	printf("%d", SumA + SumB); 
	
	return 0;
}

int p(char a[], int b) {
	int i = 0, sum = 0; 
	while(a[i] != '\0') {
		if ( (a[i] - '0') == b) {
			sum = sum * 10 + b; 
		}
		i++;	
	}
	return sum;  
}

如果是用字符数组，记得类型是%c,且a[i]里面放的是字符，要与数字相比较，就要用 a[i] - '0’变为数字

算法笔记上的方法：枚举
// Ada
#include<cstdio>

int main() {
	long long a, b, da, db;
	scanf("%lld%lld%lld%lld", &a, &da, &b, &db);
	long long pa = 0, pb = 0;
	while(a != 0) {
		if(a % 10 == da) {
			pa = pa * 10 + da;
		}
			a = a / 10;
	}
	while(b != 0) {
		if(b % 10 == db) {
			pb = pb * 10 + db;
		}
					b = b / 10;
	}
	printf("%lld\n", pa + pb);
	
	return 0;
}
1026 程序运行时间 （15 分）
  1. 题目描述 ，要获得一个 C 语言程序的运行时间，常用的方法是调用头文件 time.h，其中提供了 clock() 函数，可以捕捉从程序开始运行到 clock() 被调用时所耗费的时间。这个时间单位是 clock tick，即“时钟打点”。同时还有一个常数 CLK_TCK，给出了机器时钟每秒所走的时钟打点数。于是为了获得一个函数 f 的运行时间，我们只要在调用 f 之前先调用 clock()，获得一个时钟打点数 C1；在 f 执行完成后再调用 clock()，获得另一个时钟打点数 C2；两次获得的时钟打点数之差 (C2-C1) 就是 f 运行所消耗的时钟打点数，再除以常数 CLK_TCK，就得到了以秒为单位的运行时间。
    这里不妨简单假设常数 CLK_TCK 为 100。现给定被测函数前后两次获得的时钟打点数，请你给出被测函数运行的时间。
  2. 输入，输入在一行中顺序给出 2 个整数 C1 和 C2。注意两次获得的时钟打点数肯定不相同，即 C1 < C2，并且取值在 [0,107​​ ]。
  3. 输出，在一行中输出被测函数运行的时间。运行时间必须按照 hh:mm:ss（即2位的 时:分:秒）格式输出；不足 1 秒的时间四舍五入到秒。
  4. 样例输入,
    123 4577973
  5. 样例输出,
    12:42:59
    我的理解
    1.输入2个整数，取值在0-107
    2.要输出时、分、秒。秒数要四舍五入、
// Ada
#include<cstdio>
const int CLK_TCK = 100;
int main() {
	int c1, c2, hh, mm, ss, tt;
	scanf("%d %d", &c1, &c2);
	ss = ( c2 - c1 ) /  CLK_TCK;
	tt = ( c2 - c1 ) %  CLK_TCK;
	if( tt >= 50 ) {
		ss = ss + 1;
	} 
	hh = ss / 3600;
	mm = ( ss % 3600 ) / 60;
	ss = ( ss % 60 );

	printf("%02d:%02d:%02d", hh, mm, ss);
	
	return 0;
}

注意
1.不足1秒四舍五入----》这里得到的总秒数是总时间对100取整，则不足1秒就是对100取余。也就是整个数的后两位。即后两位>=50就总秒数+1.否则就-1.
2.得到总秒数之后，1h是3600秒，则hh = s / 3600.余下的就是总分钟。则余下的对60取整得到mm.总秒数对60取整得到的是总分钟，则余下的就是秒了。
3.一开始我是先算出小时分钟秒再判断是否要加1，这样就会有一个问题，比如总秒数为4999时，总秒数+1就变为 5000了。若不是一开始+1，得到的hh,mm,ss就会和后来再+1得到的不同。
4.注意最后一句说得到的输出格式是2位的时：分：秒。那么不足2位时前面就要补零。并规范好2位的位置。

1046 划拳 （15 分）
  1. 题目描述 ，划拳是古老中国酒文化的一个有趣的组成部分。酒桌上两人划拳的方法为：每人口中喊出一个数字，同时用手比划出一个数字。如果谁比划出的数字正好等于两人喊出的数字之和，谁就赢了，输家罚一杯酒。两人同赢或两人同输则继续下一轮，直到唯一的赢家出现。
    下面给出甲、乙两人的划拳记录，请你统计他们最后分别喝了多少杯酒。
  2. 输入，输入第一行先给出一个正整数 N（≤100），随后 N 行，每行给出一轮划拳的记录，格式为：
    甲喊 甲划 乙喊 乙划
    其中喊是喊出的数字，划是划出的数字，均为不超过 100 的正整数（两只手一起划）。
  3. 输出，在一行中先后输出甲、乙两人喝酒的杯数，其间以一个空格分隔。
  4. 样例输入,
    5
    8 10 9 12
    5 10 5 10
    3 8 5 12
    12 18 1 13
    4 16 12 15
  5. 样例输出,
    1 2
    我的理解
    1.N控制循环
    2.给出4个正整数 a, b, c, d
    3.看a + c是否 等于b或 d
    4.如果等于b则 2加1
    如果等于d则1加1
    5.输出结果
// Ada
#include<cstdio>

int main() {
	int N, a, b, c, d, P1 = 0, P2 = 0;
	scanf("%d", &N);
	while(N--) {
		scanf("%d %d %d %d", &a, &b, &c, &d);
		if ((( a + c != b ) && ( a + c ==  d ))){
			P1++;
		}
		if((( a + c  == b )&&( a + c != d ))){
				P2++;
		}
		
	} 
	printf("%d %d\n", P1, P2);
	
	return 0;
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值