数据结构——循环链表与双向链表

最新推荐文章于 2025-02-17 19:29:54 发布

Acc222222

最新推荐文章于 2025-02-17 19:29:54 发布

阅读量445

点赞数

分类专栏：数据结构C语言实现文章标签：数据结构链表

本文链接：https://blog.youkuaiyun.com/Acc222222/article/details/119348186

版权

数据结构C语言实现专栏收录该内容

10 篇文章

订阅专栏

循环链表：一种头尾相接的链表（表中最后一个结点的指针域指向头结点，整个链表形成一个环）

注：由于循环链表种没有NULL指针，故涉及遍历操作时，其终止条件就不再像非循环链表那样判断p或p->next是否为空，而是判断他们是否等于头指针。（p!=L）

1.创造循环链表

void CreateList_R(LinkList& L, int n)
{
    LNode *r, *p;//不能写成 LNode* r,p;
    L = new LNode;
    L->next = NULL;
    r = L;
    for (int i = 0; i < n; i++)
    {
        p = new LNode;
        cin >> p->data;
        p->next = NULL;
        r->next = p;//把p结点放在最后
        r = p;//更新尾指针
    }
    r->next = L;//回到头结点
}

创造循环链表一般使用尾插法——因为有一个尾指针，可以直接对尾结点进行操作。而对于头插法，如果想对尾结点进行操作，还需要遍历链表。

r->next = L;//回到头结点

在单链表尾插法的最后加上一句这个代码即可，L指向的是头结点。当然，根据情况，尾结点的指针域可以指向任何区域。

遍历示例：

int main() {
    LinkList L;//约定：LinkList用于声明表，LNode用于声明结点
    int n;
    cout << "请输入链表长度：";
    cin >> n;
    CreateList_R(L, n);
    LNode* p;
    p = L->next;
    while (p)
    {
        printf("%d ", p->data);
        p = p->next;
    }
    return 0;
}

这是与单链表相同的遍历方法：

很明显会无限循环下去。（头结点的数据域是没有内容的）

int main() {
    LinkList L;//约定：LinkList用于声明表，LNode用于声明结点
    int n;
    cout << "请输入链表长度：";
    cin >> n;
    CreateList_R(L, n);
    LNode* p;
    p = L->next;
    while (p!=L)
    {
        printf("%d ", p->data);
        p = p->next;
    }
    return 0;
}

循环条件改为：p!=L

2.带尾指针循环链表的合并

（保留La的头结点，Tb与Ta都是各自链表的尾指针）

LinkList Connect(LinkList Ta, LinkList Tb)
//Ta,Tb分别为L1，L2的尾指针,这里用尾指针来代表整个循环链表
{
    LNode* p = Ta->next;//p为L1的头结点
    Ta->next = Tb->next->next;//L1的尾结点接上L2的首元结点
    delete Tb->next;//删除L2的头结点
    Tb->next = p;//L2尾结点接上L1头结点
    return Tb;
}//Tb->next==p(也就是L1的头结点)

整体思路：首先要得出两个链表的尾指针，然后链表L1尾结点的next域指向链表L2的首元结点，链表L2尾结点的next域指向L1的头结点，删除L2的头结点。

得到尾结点的代码：

LNode* Find_R(LinkList L)
{
    LNode* p=L;
    while (p->next!=L)
    {
        p = p->next;
    }
    return p;
}//返回尾指针

当p->next==L的时候为尾指针（循环链表），把p作为返回值即可。

示例：

int main() {
    LinkList L1;//约定：LinkList用于声明表，LNode用于声明结点
    LinkList L2;
    int n,m;
    cout << "请输入第一个链表的长度和第二个单链表的长度：";
    cin >> n >> m;
    CreateList_R(L1,n);
    CreateList_R(L2,m);
    LNode *p,*q;
    p = Find_R(L1);
    q = Find_R(L2);
    LinkList L3 = Connect(p, q);
    LNode* j = L3->next->next ;//首元结点
    while (j != L3->next)
    {
        printf("%d ", j->data);
        j = j->next;
    }
    return 0;
}

1.使用尾插法创造循环链表。

2.得出两个循环链表的尾指针。

3.用L3作为合并后的链表。

4.合并后的链表状态：由于返回值为L2的尾指针，因此：

返回值->next==头结点

返回值->next->next==首元结点

根据循环链表的定义进行遍历（j!=L3->next即指针没有指向头结点时）

3.双向链表结点的定义

typedef struct DuLNode {
    int data;
    struct DuLNode* prior, * next;   
}DuLNode,*DuLinkList;

在单链表的每个结点里再增加一个指向其前驱的指针域prior，形成两个不同方向的链，称为双向链表。因此双向链表结点的定义就是在单链表的基础上加一个前驱指针域。

注：双向循环链表——1.头结点的前驱指针指向尾结点。2.尾结点的后继指针指向头结点。

4.尾插法创建双向链表

void CreateDList_R(DuLinkList& L, int n) {
    DuLNode* p, * r;
    L = new DuLNode;
    L->prior = NULL;
    L->next = NULL;
    r = L;
    for (int i = 0; i < n; i++)
    {
        p = new DuLNode;
        cin >> p->data;
        r->next = p;
        p->prior = r;
        r = p;
    }
    r->next = NULL;//双向循环链表改这个
}

（1）双向链表的初始化

L = new DuLNode;
L->prior = NULL;
L->next = NULL;
r = L;

把头结点的两个指针域都置空。r代表尾指针，刚开始指向头结点。

（2）核心代码

r->next = p;
p->prior = r;
r = p;

每次生成一个结点，放在最后（r->next=p），然后修改它的前驱（p->prior=r），最后更新尾指针即可（r=p）。

（3）最后处理

r->next = NULL;//双向循环链表改这个

把尾结点的next域置空，如果是双向循环链表的话，就需要指向头结点，然后头结点的prior域为尾结点（r->next=L,L->prior=r）。

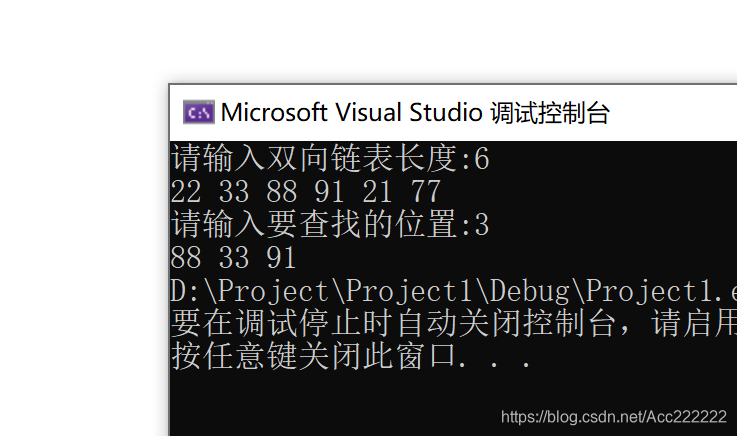
示例：输入一个位置，然后输入它，它的前驱，它的后继数据域的值

int main() {
    DuLinkList L;
    int n;
    cout << "请输入双向链表长度:";
    cin >> n;
    CreateDList_R(L, n);
    int m, i = 1;
    cout << "请输入要查找的位置:";
    cin >> m;
    DuLNode* p=L->next;
    while (p && i < m)
    {
        p = p->next;
        i++;
    }
    if (!p || i > m)
        cout << "查找失败！";
    else
    {
        if (m == n || m == 1)
            cout << "数据不合法";//要么没有后继，要么没有前驱
        else
            printf("%d %d %d", p->data, p->prior->data, p->next->data);
    }
    return 0;
}

5.双向链表的插入

int ListInsert(DuLinkList& L, int i, int e)
{
    DuLNode* p=L;
    int j = 0;
    while (p && j < i-1)
    {
        p = p->next;
        j++;
    }
    if (!p || j > i-1)
        return 0;
    DuLNode* s;
    s = new DuLNode;
    s->data = e;
    if (p->next == NULL)//要插入的前一个结点是最后一个结点
    {
        p->next = s;
        s->prior = p;
        s->next = NULL;
        return 1;
    }
    p->next->prior = s;
    s->next = p->next;
    p->next = s;
    s->prior = p;
    return 1;
}

（1）找到插入位置的前一个结点

while (p && j < i-1)
{
    p = p->next;
    j++;
}
if (!p || j > i-1)
    return 0;

其实也可以找到插入位置的结点（i），只不过后续的操作有所不同。这里为了与单链表的插入操作保持同步，也是找到第i-1个结点。

（2）生成新结点

DuLNode* s;
s = new DuLNode;
s->data = e;

（3）特殊情况处理

if (p->next == NULL)//要插入的前一个结点是最后一个结点
{
     p->next = s;
     s->prior = p;
     s->next = NULL;
     return 1;
}

如果插入的位置是尾结点后面，那么很明显会出现指针问题（NULL没有prior），因此需要做特殊处理，省略了后面结点的prior处理。（可以在第一个位置插入是因为有头结点）

（4）核心代码

  p->next->prior = s;
  s->next = p->next;
  p->next = s;
  s->prior = p;

注意顺序，有些是不能变的，建议写完后检查一下。

示例：

int main() {
    DuLinkList L;
    int n;
    cout << "请输入双向链表长度:";
    cin >> n;
    CreateDList_R(L, n);
    int e,i;
    cout << "请输入插入的数据以及位置:";
    cin >> e >> i;
    if (ListInsert(L, i, e)) {
        DuLNode* p = L->next;
        cout << "插入后的链表为:";
        while (p)
        {
            printf("%d ", p->data);
            p = p->next;
        }
    }
    else
        cout << "插入失败！";
    return 0;
}

6.双向链表的删除

int ListDelete(DuLinkList& L, int i, int& e)
{
    DuLNode* p=L;
    int j = 0;
    while (p && j < i)
    {
        p = p->next;
        j++;
    }
    if (!p || j > i)
        return 0;
    if (p->next == NULL)//删除的是最后一个结点
    {
        p->prior->next = NULL;
        e = p->data;
        delete p;
        return 1;
    }
    e = p->data;
    p->prior->next = p->next;
    p->next->prior = p->prior;
    return 1;
}

（1）找到要删除的结点

    DuLNode* p=L;
    int j = 0;
    while (p && j < i)
    {
        p = p->next;
        j++;
    }
    if (!p || j > i)
        return 0;

在单链表的删除中，是找到要删除的结点的前一个结点，因为单链表没有prior，没办法对前一个进行操作。而在双向链表中，则解决了这个问题，因此直接对要删除的结点进行操作即可。

（2）特殊情况的处理

    if (p->next == NULL)//删除的是最后一个结点
    {
        p->prior->next = NULL;
        e = p->data;
        delete p;
        return 1;
    }

特殊情况就是要删除的结点为尾结点，后面已经没有结点了，因此只需改变前一个结点的next域即可。

（3）核心代码

    p->prior->next = p->next;
    p->next->prior = p->prior;

修改删除结点前一个结点的后继和后一个结点的前驱。

示例：

int main() {
    DuLinkList L;
    int n;
    cout << "请输入双向链表长度:";
    cin >> n;
    CreateDList_R(L, n);
    int e,i;
    cout << "请输入删除的位置:";
    cin >> i;
    if (ListDelete(L,i,e)){
        DuLNode* p = L->next;
        cout << "删除后的链表为:";
        while (p)
        {
            printf("%d ", p->data);
            p = p->next;
        }
        cout << endl << "删除的元素为:" << e;
    }
    else
        cout << "删除失败！";
    return 0;
}