堆的实现及应用

原创 已于 2024-05-15 15:44:33 修改 · 668 阅读 · 14 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #算法 #c语言 #c++

于 2024-05-06 22:27:19 首次发布
本文详细介绍了堆的概念，包括逻辑结构和物理存储，以及堆的性质。讨论了堆的创建、插入、删除操作及其时间复杂度，并重点讲解了堆排序和解决TOP-K问题的方法。

目录

 堆的概念及结构

二叉树的存储结构

堆向下调整算法

堆的创建

建堆时间复杂度

堆的插入

堆的删除

堆的实现代码

堆实现的心得体会

堆的应用

 堆排序

TOP-K问题

 堆的概念及结构

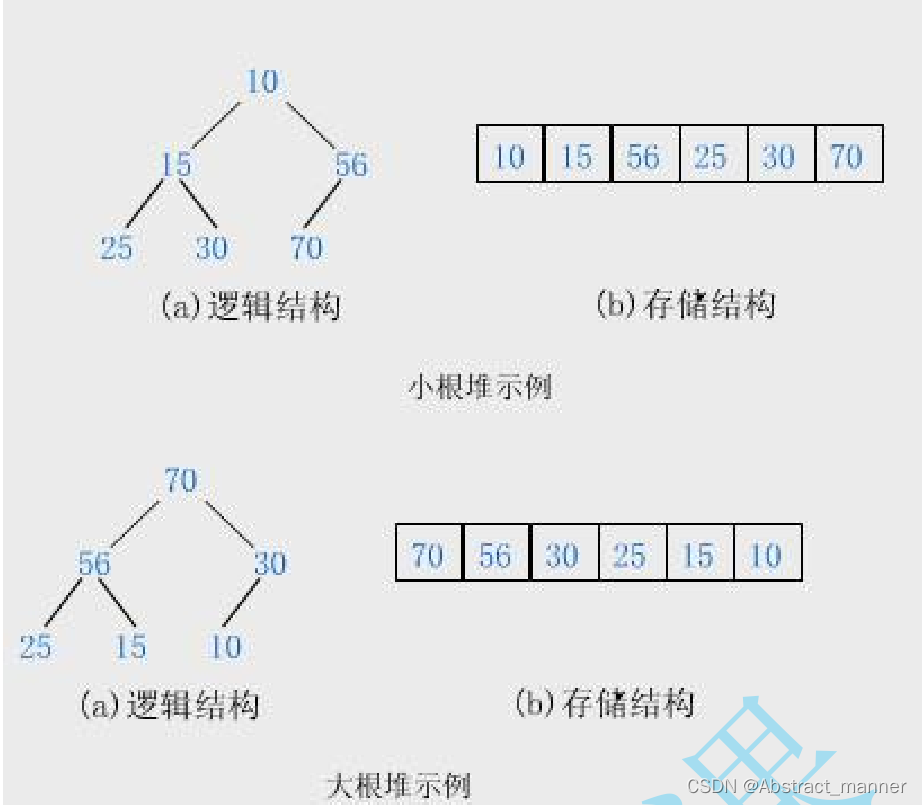
堆的逻辑结构是完全二叉树，物理存储的结构是顺序表

堆的性质：
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树

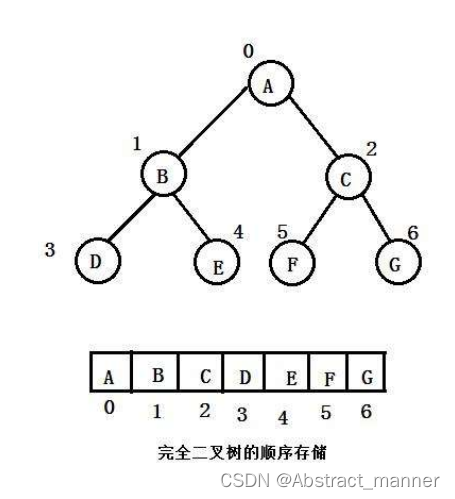
二叉树的存储结构

顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树或满二叉树，因为不是完全二叉树会有空

间的浪费。而现实中使用中只有堆才会使用数组来存储，关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

父子结点下标的规律关系

Leftchid=parent*2+1

Rightchid=parent*2+2

Parent=(child-1)/2 不区分左右孩子。

非完全二叉树就不适合数组存储结构，适合链式结构存储。

堆向下调整算法
 

现在我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整
成一个小堆。向下调整算法有一个前提：左右子树必须是一个堆，才能调整。、

void Adjustdown(HPDataType* a, int size,int parent)
{
	int child = parent * 2 + 1;
	
	while (child < size)//只是保证了孩子没有越界
	{
		if (child+1<size&&a[child] > a[child + 1])
		{
			++child;//child++的前提是child+1没有越界

		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			break;
		}

	}
	

}

堆的创建

下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算
法，把它构建成一个堆。根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的
子树开始调整，一直调整到根节点的树，就可以调整成堆。

新的建堆方法

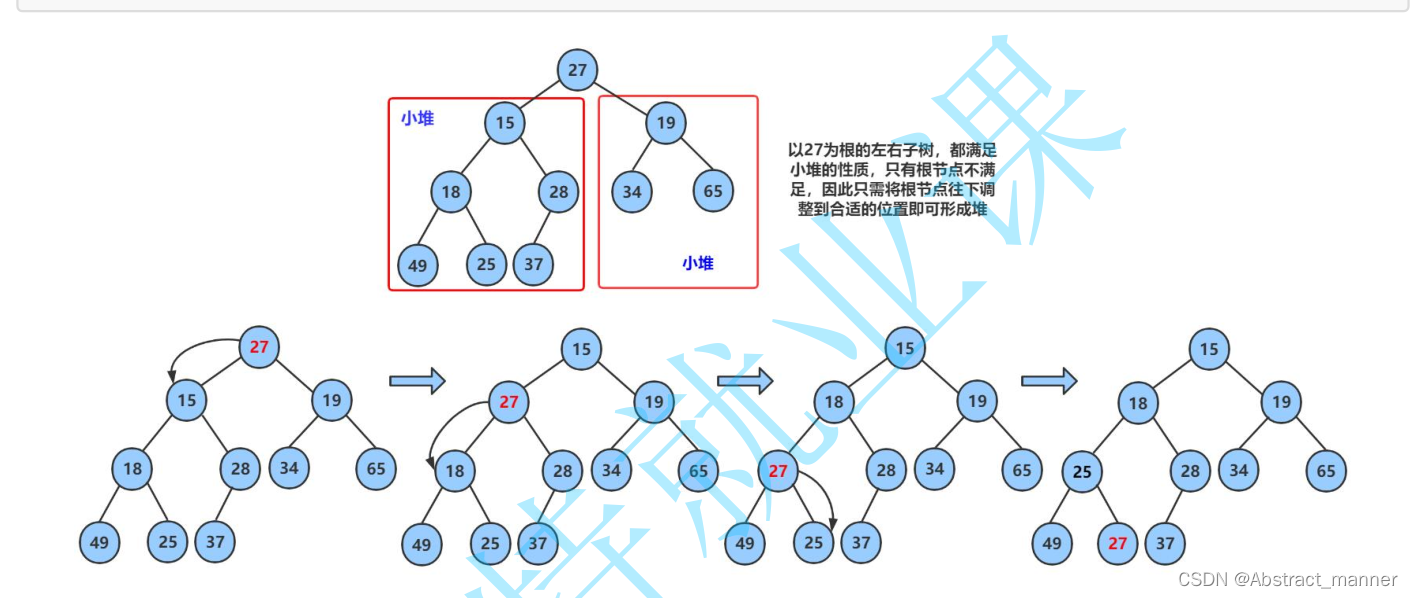
1左右子树都是小堆，向下调整即可，能变成小堆。

2如果不是，倒着调整，（目的是把左右子数都调成小堆）叶子不需要调，从倒数第一个非叶子结点开始调，也是最后一个节点的父结点。

最后一个位置是n-1，（n-1-1）/2是其父结点的下标，也是第一个非叶子结点。  

针对每一个非叶结点都能找到其子结点进行向下调整，从而使这个非叶结点所构成的子数变成小堆，随着非叶结点向上遍历与每次的向下调整，最终使左右子数都变成小堆。

   只写一个向下调整问题就能解决。效率高 时间复杂度O（N）

它的调整次数是随非叶结点的位置的变化而变化的。

建堆时间复杂度

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的
就是近似值，多几个节点不影响最终结果)：

向下调整建堆的时间复杂度

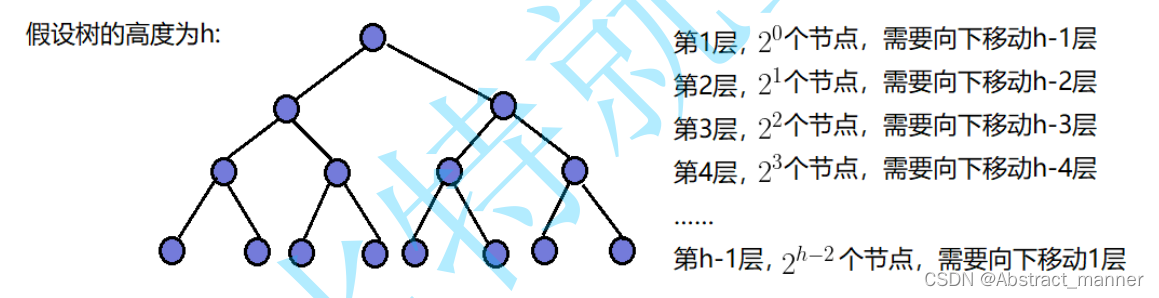
第h层：2^(h-1)个结点

第h-1层：2^(h-2)个结点

T（h）是建堆的累积调整次数

T（h）=2^(h-2)*1+2^(h-3)*2+………………….+2^0 *(h-1)等差乘等比 (错位相减法)

T(h)=2^h -1-h

 H是树的高度 N是树的节点个数

满二叉树：2^h-1=N  àh=log(N+1)

T(h)=2^h -1-h =N-log(N+1)=T(N)

因此时间是复杂度约为O（N）

向上调整建堆的时间复杂度

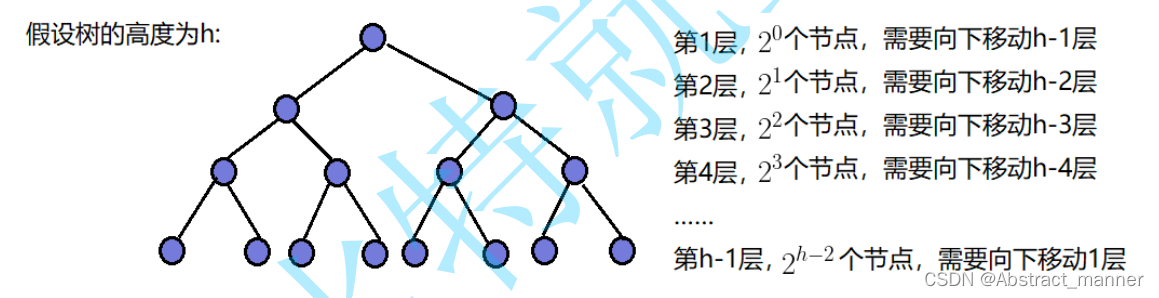
从第二层开始的原因：如果是从第一层开始的话：结点之间的伦理关系全都乱了。

从第二层往下走逐渐向上调整 二叉树的最后一层结点占一半

T（h）= 2^1*1+ 2^2*2+2^3*3………………………..+2^（h-1）*(h-1)

T(h) = -（2^h-1）+2^h*(h-1)+2^0

T(N)= -N+(N+1)*(log(N+1)-1)

与向下调整对比 一个多乘多 一个少乘多。且多了一行最多需要计算的一行，且最后一行时间复杂度就已经是O（N*logN）了。

总体的向上调整的算法复杂度O(N*logN)

选数的时间复杂度O(N*logN)

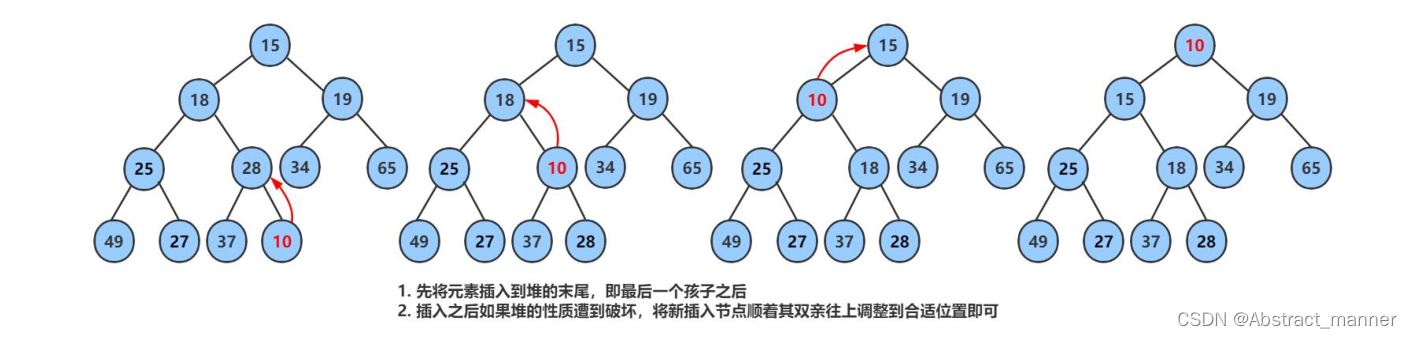
堆的插入

先插入一个10到数组的尾上，再进行向上调整算法，直到满足堆。

void Adjustup(HPDataType* a, int child)//孩子找父母 向上查找
{ 
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;

		}
		else
		{
			break;
		}
	}
}




void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->Capacity)
	{
		int newCapacity = php->Capacity == 0 ? 4 : php->Capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);

		}
		php->a = tmp;
		php->Capacity = newCapacity;

	}
	php->a[php->size] = x;
	php->size++;

	Adjustup(php->a, php->size-1);



}

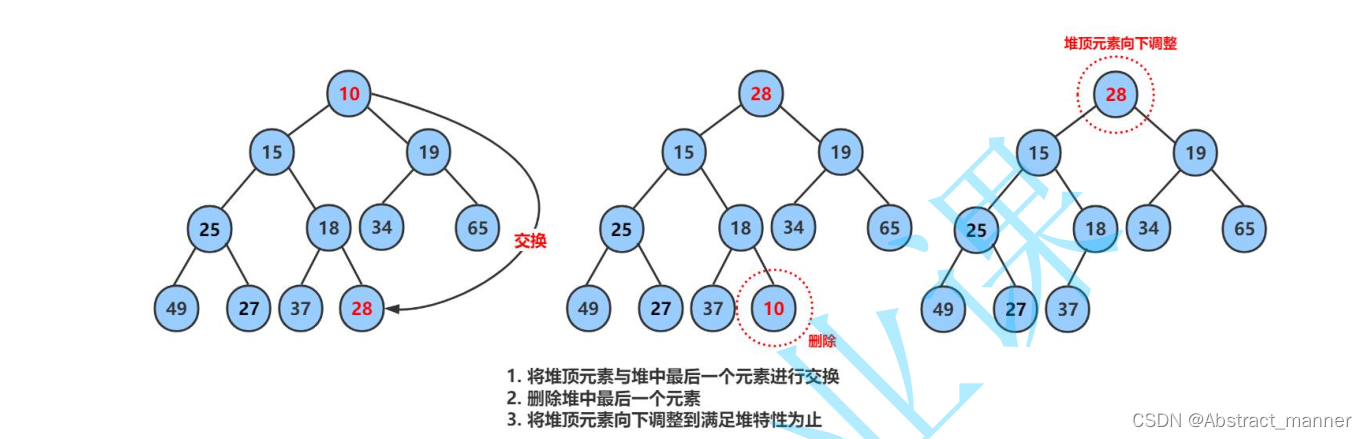
堆的删除

删除堆是删除堆顶的数据，将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。

void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	Adjustdown(php->a, php->size, 0);

}

堆的实现代码

#include<assert.h>
#include<stdbool.h>
#include<time.h>

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* a;
	int size;
	int Capacity;

}HP;

void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
size_t HeapSize(HP* php);
bool HeapEmpty(HP* php);
void Swap(HPDataType* p1, HPDataType* p2);
void Adjustup(HPDataType* a, int child);
void Adjustdown(HPDataType* a, int size, int parent);


#include"Heap.h"

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = 0;
	php->Capacity = 0;

}
void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = 0;
	php->Capacity = 0;
	
}
void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;

}

void Adjustup(HPDataType* a, int child)//孩子找父母 向上查找
{ 
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;

		}
		else
		{
			break;
		}
	}
}




void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->Capacity)
	{
		int newCapacity = php->Capacity == 0 ? 4 : php->Capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);

		}
		php->a = tmp;
		php->Capacity = newCapacity;

	}
	php->a[php->size] = x;
	php->size++;

	Adjustup(php->a, php->size-1);



}
void Adjustdown(HPDataType* a, int size,int parent)
{
	int child = parent * 2 + 1;
	
	while (child < size)//只是保证了孩子没有越界
	{
		if (child+1<size&&a[child] > a[child + 1])
		{
			++child;//child++的前提是child+1没有越界

		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			break;
		}

	}
	

}


void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	Adjustdown(php->a, php->size, 0);

}

HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}
size_t HeapSize(HP* php)
{
	assert(php);
	return php->size;

}
bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;

}

堆实现的心得体会

1 首先堆与顺序表最大的区别就是在于逻辑结构上的区别 物理上的存储是没有区别的

逻辑结构表现在数组的元素（结点）之间的伦理关系（连接关系）数字关系（大小关系）

2结构决定功能 因此在pop和push这两个功能上，堆与顺序表的差异是巨大的，且pop和push互为逆运算，因此在函数实现上也表现是相反的，push是在叶节点（最底部）增加元素，本身是child，是通过child找parent，逐渐向上做“互换”的运算，child靠parent自我运算向上跑，最后找到头结束，而pop是删除头元素（根结点），通过parent找child，逐渐向下做“互换”运算，parent靠child自我运算往下跑，直到parent的child找到尾。

因此在两个“Adjust”的传参时，都要传HP* 一个传child ，一个传parent。一个传size，一个不要传。因为头坐标为0.

堆的应用

 堆排序
 

1. 建堆
升序：建大堆
降序：建小堆
2. 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

void Heapsort(int* a, int n)
{
	//建大堆
	//向上调整算法 时间复杂度NlogN
	/*for (int i = 1; i >= 0; i++)
	{
		Adjustup(a, 1);

	}*/

	//向下调整算法
	int end = n - 1;
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		Adjustdown(a, n, i);


	}
	//调整成大堆之后在数组中实际上是降序排列的，所以要借助删除函数的思想，进行交换操作

	while (end > 0)
	{
		Swap(&a[end], &a[0]);
		Adjustdown(a, end, 0);//首尾元素交换之后，新的尾元素就是本次操作的最大元素，应将其排除堆，所以这里end=n-1正好是排除堆后新的size
		--end;
	}

}

TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：
1. 用数据集合中前K个元素来建堆
前k个最大的元素，则建小堆
前k个最小的元素，则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

具体思考：

1读取前K个值，建立K个树的小堆

2、依次再读取后面的值，跟堆顶比较，如果比堆顶大，替换对顶进栈（替换堆顶值，再向下调整） 用小堆的精髓就是最大的前K个在进堆时，一定有比上来给的前K个要大（个体与个体比），一定能够进堆，然后较大的数会因为向下调整算法不断下沉。

空间复杂度就是k大小的堆 

时间复杂度：O（N*logK）

void CreateNDate()
{
	// 造数据
	int n = 10000000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (int i = 0; i < n; ++i)
	{
		int x = (rand() + i) % 10000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}


void HeapTopK(const char* file,int k)
{
	FILE* fout = fopen(file,"r");

	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}

	int* minheap = (int*)malloc(sizeof(int)*k);
	if (minheap == NULL)
	{
		perror("malloc fail");
		return;
	}

	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &minheap[i]);
		Adjustup(minheap, i);

	}
	int x = 0;
	while (fscanf(fout, "%d", &x) != EOF)
	{
		/*if (x > 10000000)
		{
			int bb = 0;
		}*/
		if (x >= minheap[0])
		{
			minheap[0] = x;
			Adjustdown(minheap, k, 0);
		}
	}
	for (int i = 0; i < k; i++)
	{
		printf("%d ", minheap[i]);

	}
	printf("\n");
	free(minheap);
	fclose(fout);
}

评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值