本文详细探讨了Huffman编码的实质，包括无失真信源编码策略，以及半自适应和自适应统计模型的编码与解码方法。特别关注了半自适应模型中编码表的生成算法和解码过程，以及在图像压缩中的实践应用。
补充：
无失真信源编码的实质
对离散信源进行适当的变换，是变换后新的符号序列信源尽可能为等概分布，从而使新信源的每个码符号平均所含信息量达到最大！
Huffman算法概述
Huffman编码的分类
- 静态统计模型
- 码表根据训练数据得到，不同信源利用同一个概率表
- 无需传送Huffman码表/码树
- 半自适应统计模型
- 对每个输入信源符号，计算其概率
- 需要对输入进行两边扫描，无法适应于实时传输
- 必须传送Huffman码表和压缩流
- 自适应/动态统计模型
- 一遍扫描
- 当频率改变时，改变Huffman码表/树
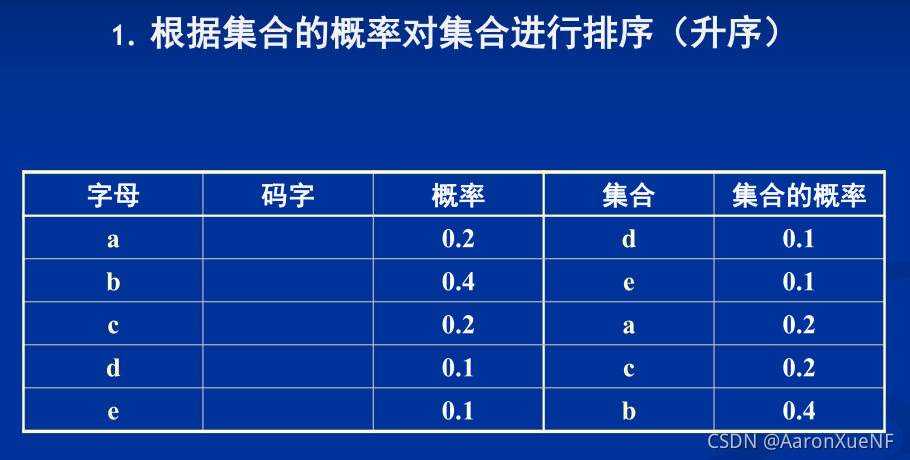
半自适应统计模型的Huffman码表生成算法：
- 第一次计算所有符号的频率/概率
- 对所有符号按其概率排序
- 将符号集合划为为两个概率差异最小集合
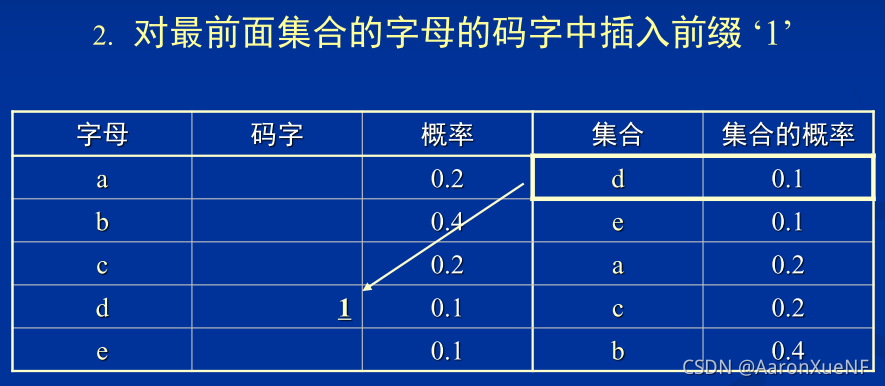
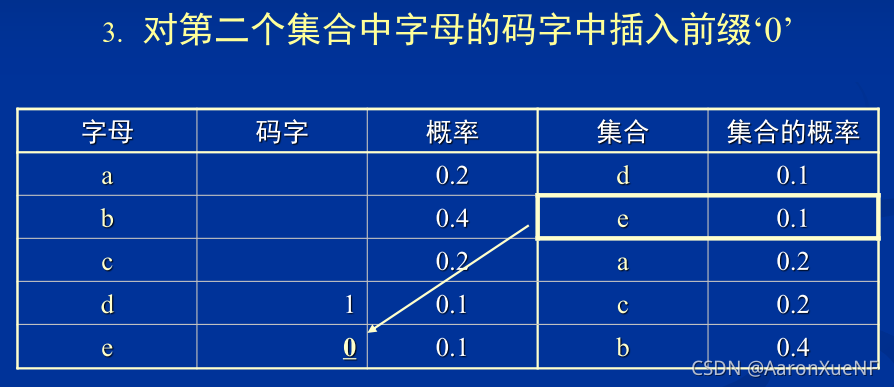
- 在第一个集合的码字前加‘0’，在第二个集合的码字前 加‘1’
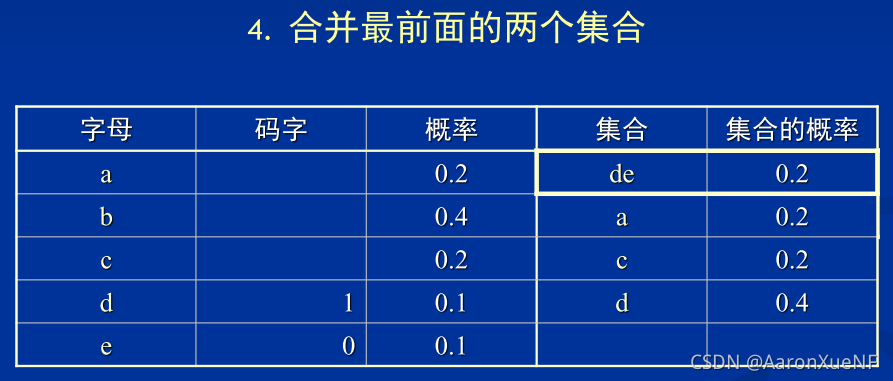
- 对划分得到的两个子集递归编码，直到每个集合不能被再划分
Huffman解码
对于半自适应统计模型的Huffman需要传送码表吗，通常在文件中写入频率/概率，即将频率/概率标定为整数，然后解码器利用该信息构造Huffman树，这相比于写入Huffman树结构可以有更小的比特开销。
Huffman解码通常有两种方式：
- 比特串行解码：固定输入比特率，可变输出符号率
- 从码树根节点出发，根据逐个读入的比特走过各节点（通过0、1确定下一个走过的是左子树还是右子树），直至走到树叶，输出树叶的字符，回到根节点继续。
- 基于查找表的解码
- 对于最长码字为l比特，构造2l个入口的查找表。假设x对应码字w长为3，为“001”，最长码字长为5，则查找表中对应x的记录有4项：“001xx”（后两位任意）。
- 解码时一次读入l比特，从前到后在码表中查找对应，找到则输出相应码字（假设码长为w），并移除前w个比特，读入w个比特。
基于查找表的解码
规范Huffman编码
规范的本质是数据结构化问题！
使用某些强制的约定，仅通过很少的数据便能重构出霍夫曼编码树的结构。
一种典型的规范Huffman编码方式如下：
- 使用某种算法，统计每个符号的频率并求出该符号所需的位数/编码长度
- 统计从最大编码长度到1的每个长度对应多少个符号，然后为每个符号递增分配编码
- 码字长度最小的第一个编码从0开始
- 长度为i的第一个码字f(i)能从长度为i-1的最后一个码字得出, 即: f(i) = 2(f(i-1)+1)。假定长度为4的最后 一个码字为1001，那么长度为5的第一个码字便为10100
- 编码输出压缩信息
简言之：相同码长的码，依次按二进制+1；码长增加时，+1补0，这点从下面例子很容易看出来。
其中，需要3个关键列表：
first[i] : 码长为i的第一个码字
index[j] : 第一个码长为j的符号索引
Table[k] : 索引为k的码字
举例如下：
从例子中可知，在当前的规范下，只要识别到了一个码字的码长l，将其与第一个码长l码字相减的二进制数即为其相较于第一个码长l的码字在索引中的偏移！
自适应Huffman编码算法
自适应Huffman编码中，编码器和解码器都从一棵空的码树开始，随着符号的读入按相同的方式修改码树。
- 所有的节点分为两类：树叶节点（对应实际的信源符号）和中间节点（对应中间合并的结果）；
- 树叶节点的权重即为其对应的信源符号出现的次数。中间节点的权重是其子节点权重的和。节点编号是为每个节点分配的唯一编号。如果有n个信源符号，则共有2n-1个节点（包含树叶节点和中间节点）。
动态霍夫曼码树的两条决策原则：
- 权重值大的节点，其节点编号也较大；
- 父节点的节点编号总是大于其子节点的节点编号。
动态霍夫曼码树的初始化问题：
- 在初始化编码树时，不知道各种信源符号频率。设置一个节点，称为NYT（Not Yet Transmitted，尚未传送），其权重为0，用一个逃逸码（escape code）表示，与任何一个要传送的符号不同。发送器和接收器的树都从只有一个节点（NYT）开始。
- 在编码过程中，如果输入未包含在码树中的符号，编码器一边更新编码树，同时输出NYT码字加上符号的原始表达。解码器收到一个NTY之后，将后一个码字识别为符号加入码树中。
算法过程：
更新过程要求节点保持固定顺序，即从NYT节点到根节点的编号始终从左向右、自下而上递增。
定义权值相同的一组节点组成一个块。
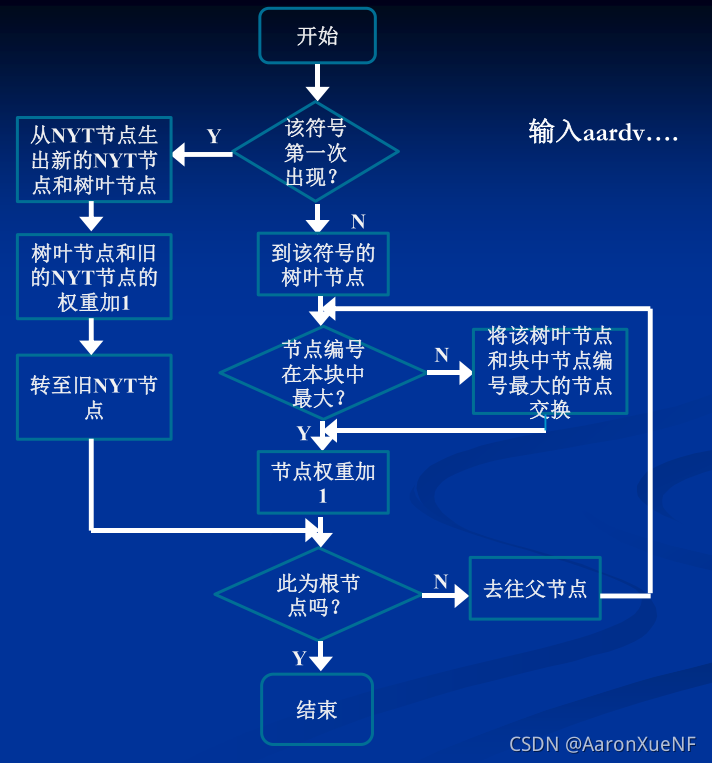
举例：
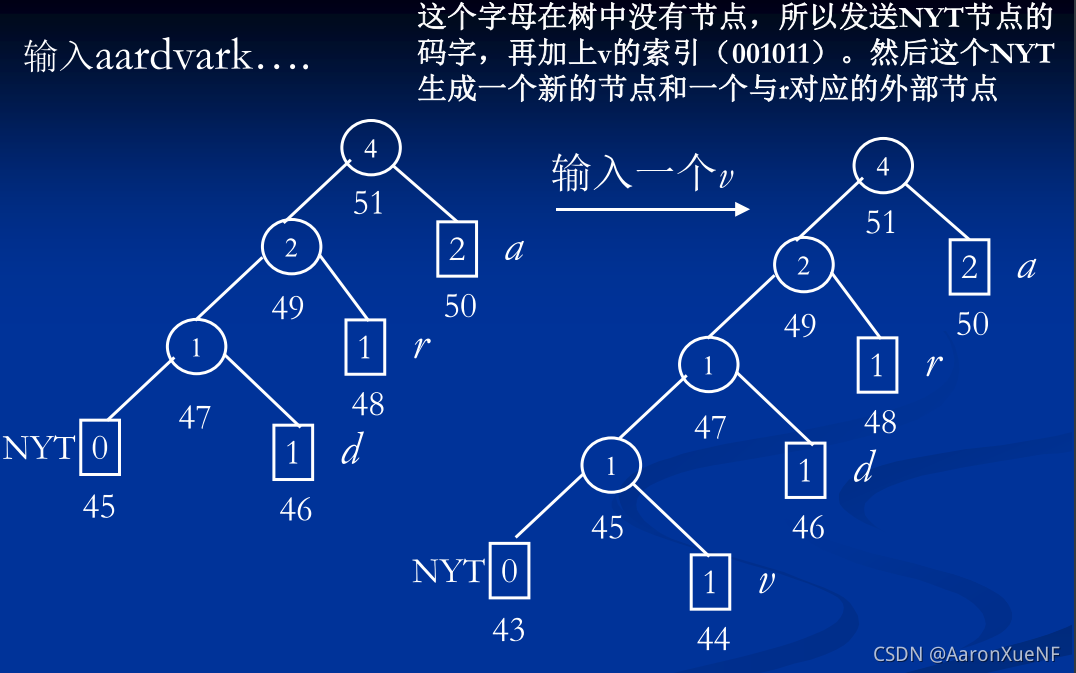
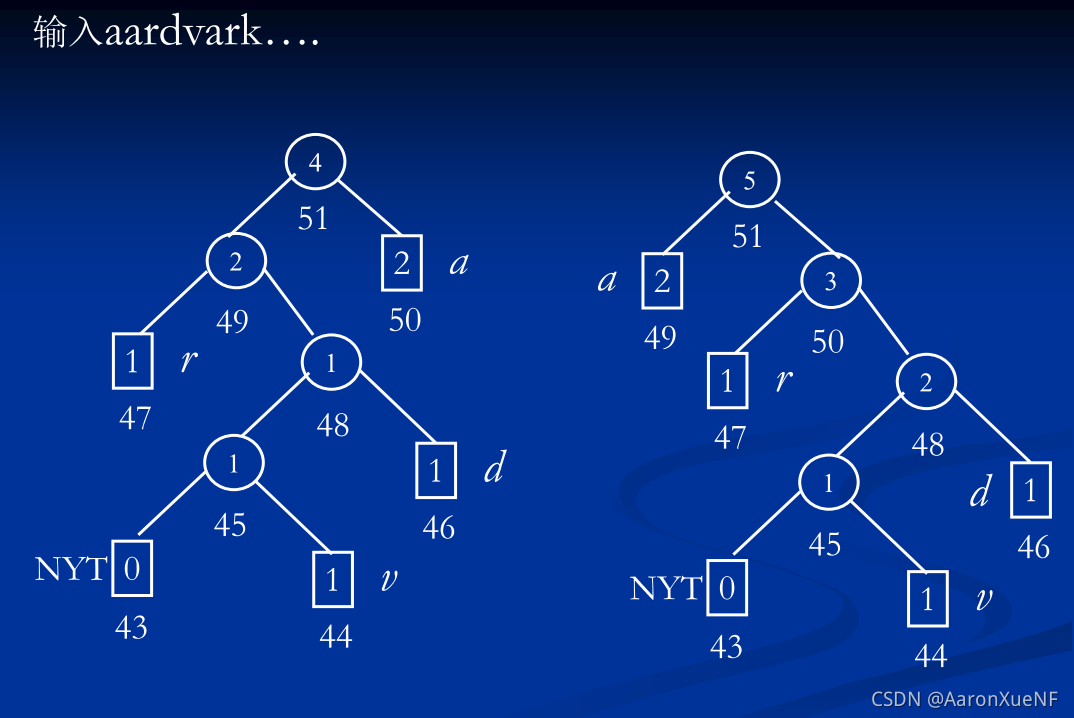
四个图为给定码树后插入字符v按照算法框图执行的过程。
Huffman编码实验内容
使用《数据压缩导论（第四版）》中的示例程序进行以下操作：
- 使用huff_enc对Sena、Sensin、Omaha图像进行编码；
- 编写程序，得到相邻像素之差，使用huff_enc对其进行编码；
- 利用huff_enc和huff_dec生成图像Sensin的码表，使用该码表对BookShelf1和Sena图像进行编码，并将编码结果与各图像自身码表的编码结果进行对比。
实验素材
实验所用图像：
未经压缩的256 * 256像素8位灰度图，其各像素值按光栅扫描顺序存储。
Sena
Sensin
Omaha
Bookshelf
实验所用程序：
- 《数据压缩导论（第四版）》中的示例程序huff_enc、huff_dec，程序分析见文章结尾；
- 自行编写的DPCM编码程序（使用左侧像素预测）；
- 自行编写的8位灰度图像查看程序。
实验结果
1. Huffman编码结果
| 图像名称 | 原始文件大小 | 压缩文件大小 | 压缩率 |
|---|---|---|---|
| Sena | 64kB | 56.1kB | 87.66% |
| Sensin | 64kB | 59.9kB | 93.59% |
| Omaha | 64kB | 57.0kB | 89.06% |
结论：
在仅使用Huffman编码的情况下图像压缩程度有限。
2. 像素差值文件编码结果
预测图像举例（以Sensin为例）
| 图像名称 | 原始文件大小 | 直接压缩文件大小 | 预测后压缩文件大小 | 原始压缩率 | 预测后压缩率 |
|---|---|---|---|---|---|
| Sena | 64kB | 56.1kB | 32.4kB | 87.66% | 51.56% |
| Sensin | 64kB | 59.9kB | 37.8kB | 93.59% | 59.38% |
| Omaha | 64kB | 57.0kB | 51.4kB | 93.59% | 80.31% |
结论：
在DPCM预测编码与Huffman编码联合使用的情况下图像压缩程度相较于仅使用Huffman编码有了明显提升。证明DPCM的预测可以有效地利用像素值间的相关性，预测后的差值信号近似于拉普拉斯分布，即信源符号在个别取值上较为集中，使其更适应于Huffman编码的方式。
3. 使用不同码表对图像进行编码
| 图像名称 | 原始文件大小 | 压缩文件大小 | 压缩率 |
|---|---|---|---|
| Sena | 64kB | 59.2kB | 92.50% |
| Bookshelf1 | 64kB | 70.8kB | 110.63% |
结论：
使用Sensin图像的Huffman码表对Sena、BookShelf图像进行编码时图像压缩率均出现了下降。其中，通过观察可知Sena与Sensin图像在整体像素值分布上较为近似，因此压缩率下降较小；而Bookshelf1图像在像素值上与Sensin图像差异较大，因此压缩率下降明显，甚至出现压缩图像大于原始图像的现象。这说明进行Huffman编码时要求码表中各符号概率与信源符号概率严格匹配。因此对于基础的Huffman压缩算法，需要在压缩前统计文件符号概率并在压缩后将码表一并输出。
程序分析
分析添加在程序的注释中。
自行编写的DPCM编码程序（使用左侧像素预测）
imgdiff.cpp
#include <fstream>
#include <iostream>
using namespace std;
void usage()
{
cout << "Usage:\n" << endl;
cout << "imgdiff [infile][width][height][outfile]\n" << endl;
cout << "\t infile : Input raw img file. \n" << endl;
cout << "\t width : width of img. \n" << endl;
cout << "\t height : height of img. \n" << endl;
cout << "\t outfile : Out img contains the diffence between pixels\n" << endl;
}
inline int index(int x, int y, int width)
{
return y * width + x;
}
inline uint8_t clip255(int x)
{
x = x + 127;
if (x >= 255)
return UINT8_MAX;
else if (x <= 0)
return 0;
else
return x;
}
int main(int argc, char** argv)
{
if (argc != 5) {
usage();
}
/* Read image file */
ifstream img_in(argv[1], ios::binary);
_ASSERT(img_in.is_open());
uint16_t width = atoi(argv[2]);
uint16_t height = atoi(argv[3]);
uint8_t* img_data = new uint8_t[width * height];
_ASSERT(img_data);
// Check file size
istream::pos_type start_pos = img_in.tellg();
img_in.seekg(0, ios_base::end);
istream::pos_type end_pos = img_in.tellg();
img_in.seekg(start_pos);
istream::pos_type file_size = end_pos - start_pos;
_ASSERT(file_size, width * height);
img_in.read((char*)img_data, width * height);
img_in.close();
/* Calculate diff img */
uint8_t* diff_data = new uint8_t[width * height];
_ASSERT(diff_data);
for (int y = 0; y < height; y++) {
diff_data[index(0, y, width)] = img_data[index(0, y, width)];
for (int x = 1; x < width; x++) {
int diff = img_data[index(x, y, width)] -
img_data[index(x - 1, y, width)];
diff_data[index(x, y, width)] = clip255(diff);
}
}
/* Save diff file */
ofstream diff_out(argv[4], ios::binary);
_ASSERT(diff_out.is_open());
diff_out.write((char*)diff_data, width * height);
diff_out.close();
delete[] img_data;
delete[] diff_data;
return 0;
}
自行编写的8位灰度图像查看程序（matlab）
imgshow.m
clear; close all; clc;
%% definition of size
M = 256;
N = 256;
%% definition of filepath
pathname = ".\images\diff"; % 文件路径
filename = "\sensin_diff.img"; % 文件名称
%% read files
f = fopen(pathname + filename, 'r');
data = fread(f, 'uint8');
fclose(f);
len = length(data);
k = len/(M*N);
image = uint8((reshape(data, M, N, k))');
%% show
imshow(uint8(image));
《数据压缩导论（第四版）》中的示例程序huff_enc、huff_dec
idc.h
#pragma once
#include <string.h>
#include "getopt.h"
#include "unistd.h"
/* define the structure node */
struct node {
float pro; /* probabilities */
int l; /* location of probability before sorted */
unsigned int code; /* code */
struct node* left; /* pointer for binary tree */
struct node* right; /* pointer for binary tree */
struct node* forward;
struct node* back;
struct node* parent; /* pointer to parent */
int check;
};
/* define subroutines and pointers to nodes */
typedef struct node NODE;
typedef struct NODE* BTREE;
BTREE create_list(float prob[], int loc[], int num);
void create_code(NODE* root, int lgth, unsigned int* code, char* length);
//BTREE make_list(int num);
//void write_code(NODE* root, int lgth, unsigned int* code, char* length, int* loc);
void sort(float* prob, int* loc, int num);
void huff(float prob[], int loc[], int num, unsigned int* code, char* length);
void getcode(FILE* fp, int num, unsigned int* code, char* length);
void value(int* values, unsigned char* image, int size, int num);
int files(int size, int* code, char* length, unsigned char* file);
huff_enc.c
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include "idc.h"
/**********************************************************************
* *
* File: huff_enc.c *
* Function: Huffman encodes an input file assuming a 256 letter *
* alphabet *
* Author : S. Faltys *
* Last mod: 7/21/95 *
* Usage: see usage(), for details see man page or huff_enc.doc *
* *
***********************************************************************/
/*******************************************************************************
*NOTICE: *
*This code is believed by the author to be bug free. You are free to use and *
*modify this code with the understanding that any use, either direct or *
*derivative, must contain acknowledgement of its author and source. The author*
*makes no warranty of any kind, expressed or implied, of merchantability or *
*fitness for a particular purpose. The author shall not be held liable for any*
*incidental or consequential damages in connection with or arising out of the *
*furnishing, performance, or use of this software. This software is not *
*authorized for use in life support devices or systems. *
********************************************************************************/
void usage(void);
void main(int argc, char** argv)
{
unsigned char* file; /*pointer to an array for file */
char infile[80], outfile[80], codefile[80], scodefile[80];
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
