第二讲：完全背包

在01背包的基础上，每种物品都无限件可以使用。

样例://来源：http://ybt.ssoier.cn:8088/problem_show.php?pid=1268

设有n种物品，每种物品有一个重量及一个价值。但每种物品的数量是无限的，同时有一个背包，最大载重量为M，今从n种物品中选取若干件(同一种物品可以多次选取)，使其重量的和小于等于M，而价值的和为最大。

【输入】

第一行：两个整数，M(背包容量，M≤200)和N(物品数量，N≤30)；

第2..N+1行：每行二个整数Wi,Ci，表示每个物品的重量和价值。

【输出】

仅一行，一个数，表示最大总价值。

【输入样例】

10 4
2 1
3 3
4 5
7 9

【输出样例】

max=12

在01的基础上，我们所取的物品不在只有1件，而是有无数件，如果单纯的按照01背包的思路来解，加一层循环k，来判断取第k件时候能否成功，这样的话时间复杂度会达到O(V*Σ(V/c[i]))，是比较大且不可取的。

这里给出O(vn)的算法：f[i][v]=max{f[i-1][v],f[i][v-c[i]]+w[i]}

你会发现，这个代码只和01代码在取的时候有区别，我们在01背包的时候，考虑的是取第i件时候，所以放在第i-1上决策，而对于无穷多的物品，我们是考虑我们第i件物品取了1次，2次，只要空间足够，我们就一直会考虑是否能再取，基于第i件的物品决策，所以后面取的情况是f[i][v-c[i]],这里有个很重要的地方：这里的v是从0开始，而01背包的v是从最后开始。

先阐述一下原理，如果从后开始取，我们是基于前面的f[v-c[i]]的位置，但是由于是从后面取的，所以当我们max（f[v],f[v-c[i]]+w[i]）的时候，f[v-c[i]]其实是上i的值，即对应i-1的时候，所以对于01背包，我们可以运用，但是对于完全背包，我们需要的是当前取第i种物品的情况，所以只要满足空间足够，我们就要考虑要多加一件i物品的可能，所以从前开始，此时针对的是第i件物品做决策，如果听着还是有点困难的话，下面给出上面数据的表：//来源：一个小伙伴的博客

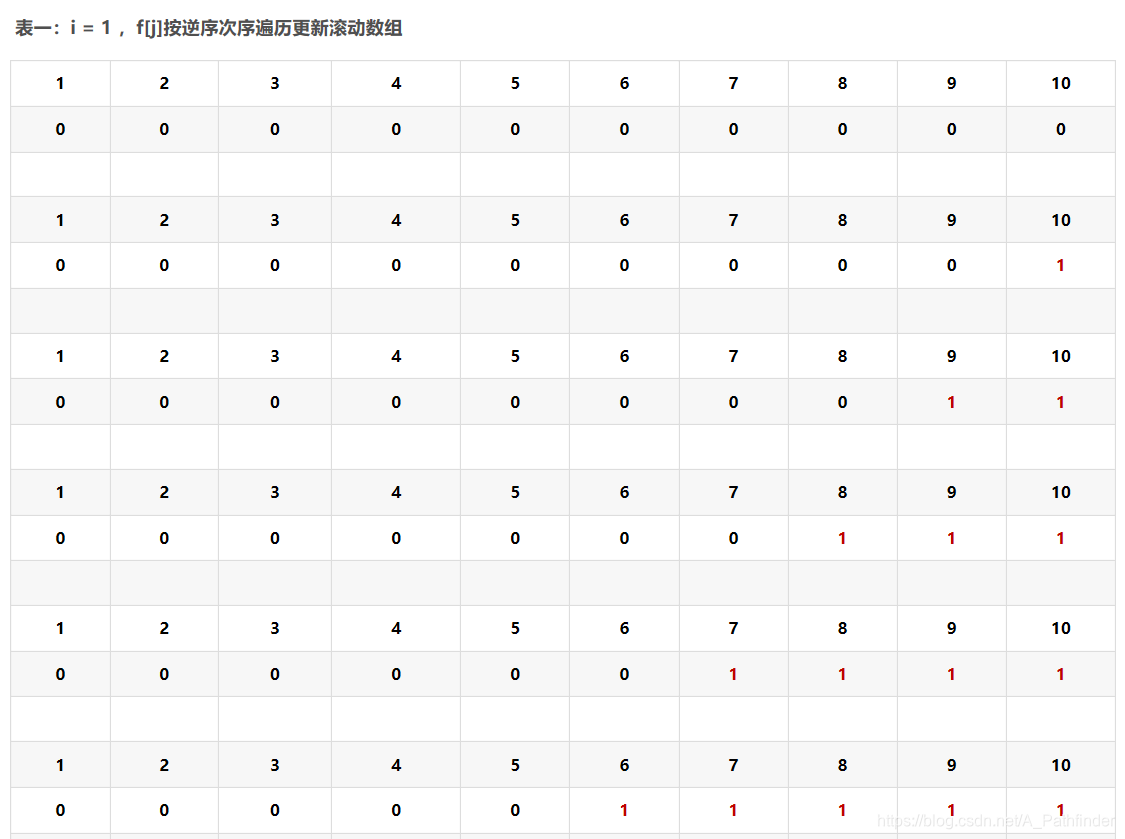
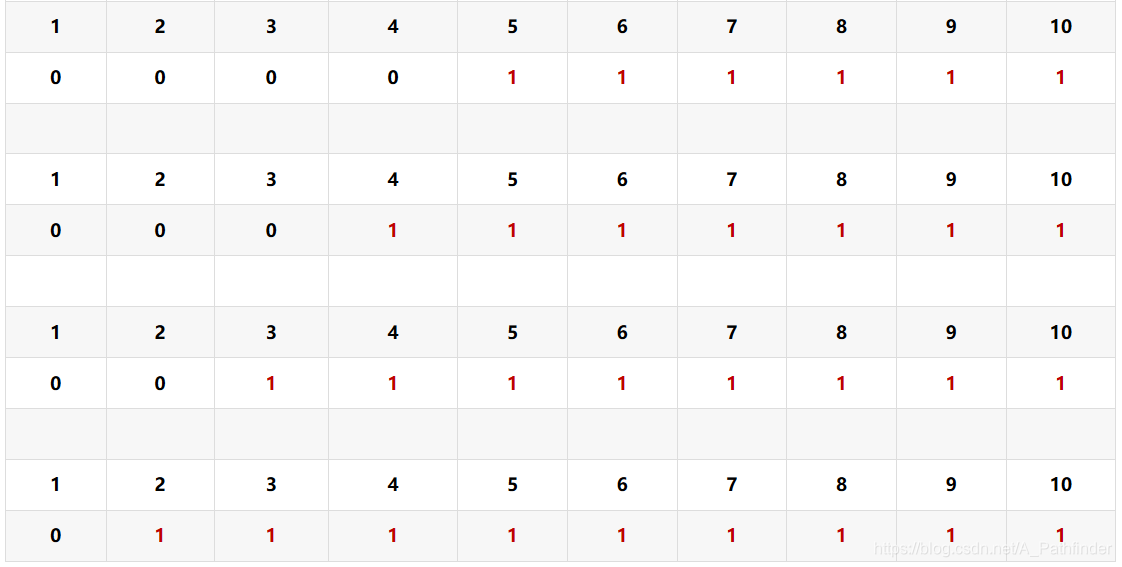
这对应的是01背包的情况，每次改变都对应i-1的情况

再看看完全背包从前往后：

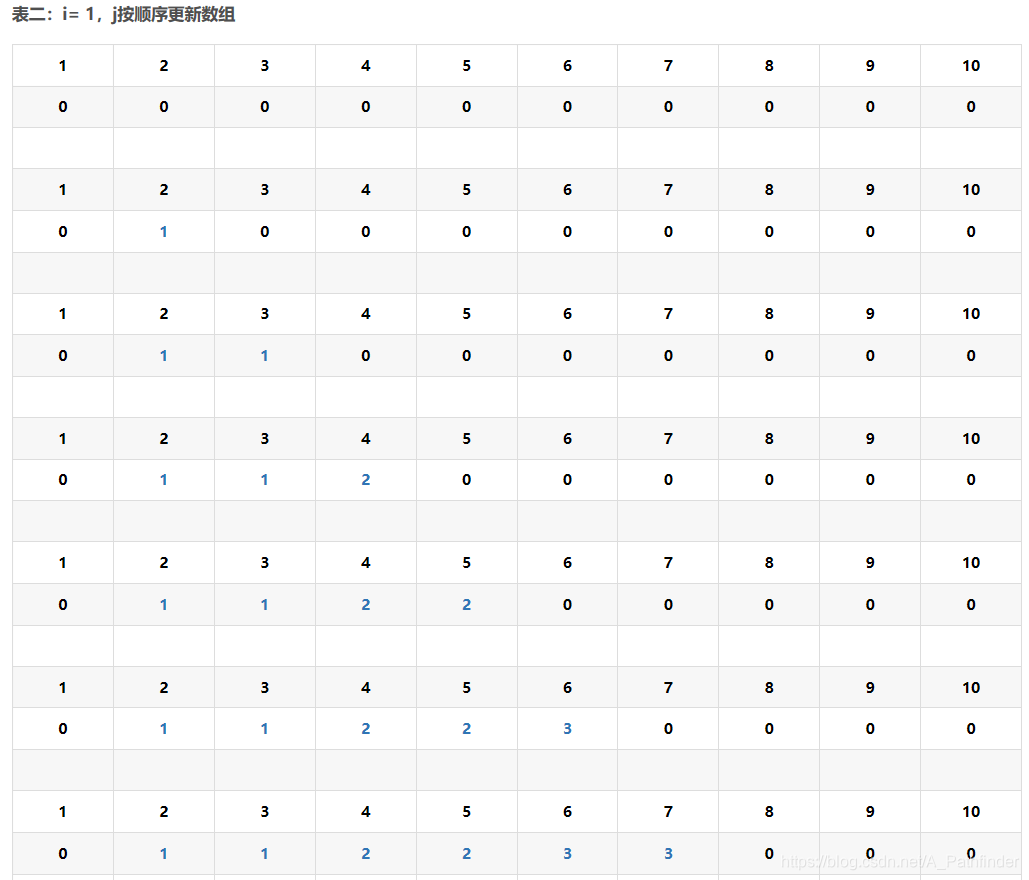
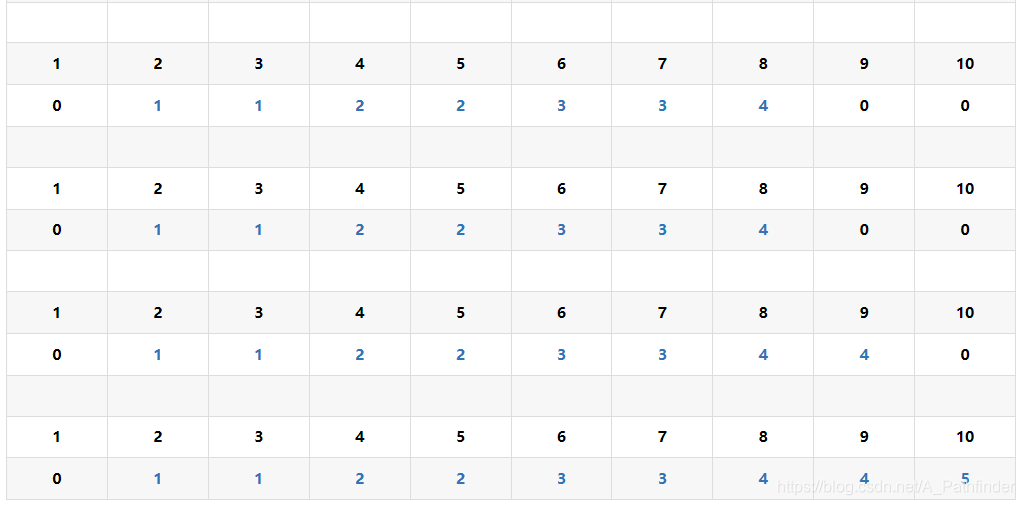
不难发现，我们所选的f[v-c[i]]在每次空间足够放下另一个i物品的时候，都会取进行判断选取，所以针对的情况是选i物品的时候。

优化：

和01背包的优化思维方式一样，针对

f[i][v]=max（f[i-1][v],f[i][v-c[i]]+w[i]）

得到一维优化

if(f[v-w[i]]+c[i]>f[v]) f[v]=f[v-w[i]]+c[i];

给出代码：

二维：

#include<bits/stdc++.h>
using namespace std;
int f[35][250],w[35],c[35];
int main(){
	int m,n;
	scanf("%d %d",&m,&n);
	for(int i=1;i<=n;i++)
	scanf("%d %d",&w[i],&c[i]);
	
	for(int i=1;i<=n;i++){
		for(int v=1;v<=m;v++){
			if(v<w[i]) f[i][v]=f[i-1][v];
			else{
				if(f[i-1][v]>f[i][v-w[i]]+c[i]) f[i][v]=f[i-1][v];
				else f[i][v] = f[i][v-w[i]]+c[i];
			}
		}
	}
	printf("max=%d",f[n][m]);
	return 0;
}

一维：

#include<bits/stdc++.h>
using namespace std;
int f[250],w[35],c[35];
int main(){
	int m,n;
	scanf("%d %d",&m,&n);
	for(int i=1;i<=n;i++)
	scanf("%d %d",&w[i],&c[i]);
	
	for(int i=1;i<=n;i++){
		for(int v=w[i];v<=m;v++){
			if(f[v-w[i]]+c[i]>f[v]) f[v]=f[v-w[i]]+c[i];
		}
	}
	printf("max=%d",f[m]);
	return 0;
}

总结：完全背包问题也是一个相当基础的背包问题，它有两个状态转移方程，分别在“基本思路”以及“O(VN)的算法“的小节中给出。希望你能够对这两个状态转移方程都仔细地体会，不仅记住，也要弄明白它们是怎么得出来的，最好能够自己想一种得到这些方程的方法。事实上，对每一道动态规划题目都思考其方程的意义以及如何得来，是加深对动态规划的理解、提高动态规划功力的好方法。