求连通分量 （01迷宫 全球变暖）

求连通分量一般用dfs,bfs和并查集

给出第一题：o1迷宫 题目来源：https://www.luogu.org/problemnew/show/P1141

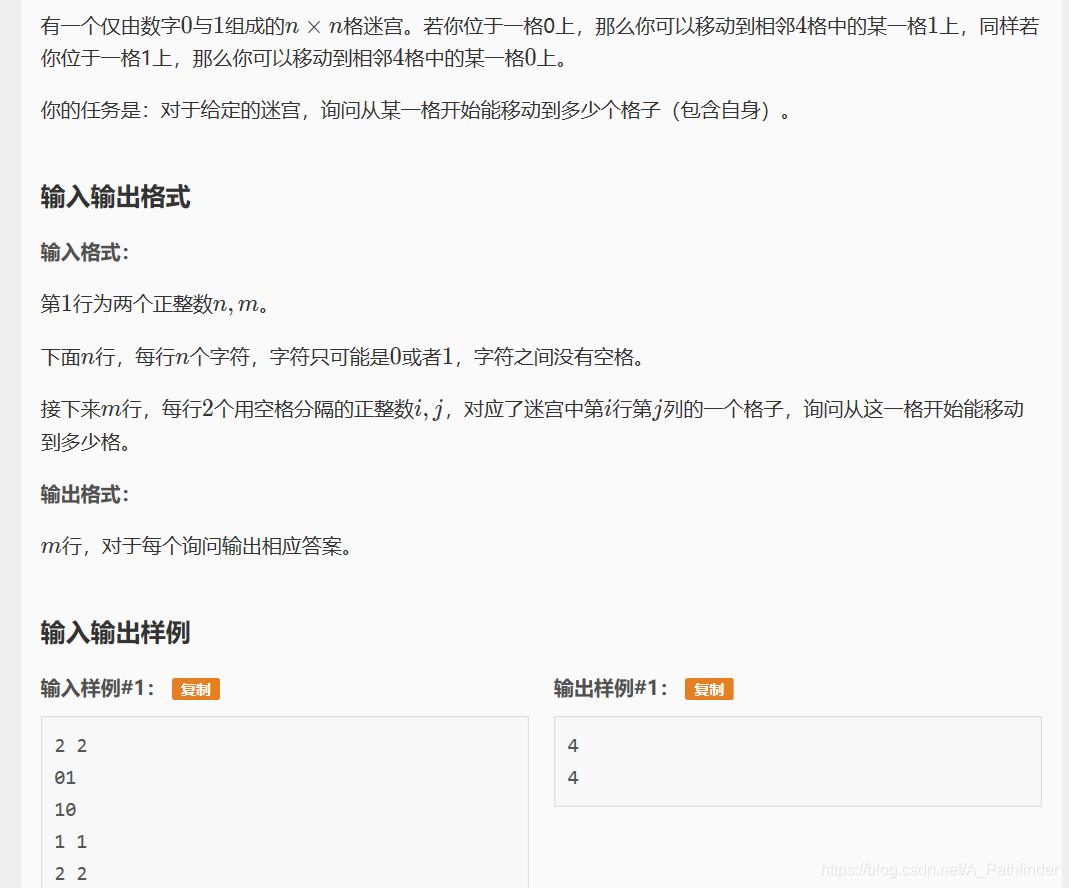
思路：用dfs确定连通度，用并查集维护连通块个数。

这里类似并查集的思路都是解决点到父亲数组的映射，也就是把二维数组变成一维数组：f[x*n+y]=x*n+y;//n是列数

把连通块里所有的点总数放在祖宗节点上，这样查询任意点所在连通块的个数就简化成查询这个点祖宗的个数。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1010;
int h[maxn*maxn],f[maxn*maxn];
char mp[maxn][maxn];
int dir[5][3]={{0,1},{1,0},{-1,0},{0,-1}};
int n,m;
int find(int x){
	return x==f[x]?x:f[x]=find(f[x]);
}
void un(int a,int b){
	int fa=find(a);
	int fb=find(b);
	if(fa!=fb){
		h[fb]+=h[fa]; // 不能反这里，是把fa变成fb的儿子，那么把以fb为祖宗的节点个数加到以fa为祖宗的数上 
		f[fa]=fb;
		return;
	}
	return;
}
void init(){
	memset(f,-1,sizeof f);
	scanf("%d %d",&n,&m);
	for(int i=0;i<n;i++)
	scanf("%s",mp[i]);	
}
int dfs(int x,int y){
	if(f[x*n+y]!=-1) return find(x*n+y);
	f[x*n+y]=x*n+y,h[x*n+y]=1;//构造映射 
	for(int i=0;i<4;i++){
		int nx=x+dir[i][0];
		int ny=y+dir[i][1];
		if(mp[x][y]!=mp[nx][ny] && nx>=0 &&ny>=0&&nx<n&&ny<n){
			un(x*n+y,dfs(nx,ny)); //合并这个连通块 
		}
	}
	return find(x*n+y); //返回父亲节点 
}
void solve(){
	while(m--){
		int x,y;
		scanf("%d %d",&x,&y);
		printf("%d\n",h[dfs(x-1,y-1)]);////查询点所在连通快的个数 
	}
}
int main(){
	init();
	solve();
	return 0;
} 

---

全球变暖（bfs求连通块+染色+去重）

题目来源：2018年蓝桥杯省赛

思路：先用bfs找出连通分量，在找分量的时候顺便记录下这个分量应该的染色和在这个分量上哪些点不会被侵蚀，再去重不会被侵蚀的点上颜色（原来所在的连通分量），最后用开始的连通块个数，减去去完重后的连通块个数，就是结果。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1010;
typedef pair<int,int> P;
char mp[maxn][maxn],mp2[maxn][maxn];
int col[maxn][maxn],dir[5][3]={{1,0},{0,1},{0,-1},{-1,0}};
int n,res;
set<int> st;
void init(){
	scanf("%d",&n);
	for(int i=0;i<n;i++){
		scanf("%s",&mp[i]);
		strcpy(mp2[i],mp[i]);
	}
}
bool in(int x,int y){
	if(x<0||x>n||y<0||y>n) return false;
	return true;
}
void bfs(int x,int y,int res){
	P p({x,y});
	queue<P> q;
	q.push(p);
	while(!q.empty()){
		P d=q.front();
		q.pop();
		int x=d.first,y=d.second;
		col[x][y] = res;
		for(int i=0;i<4;i++){
			int nx=x+dir[i][0];
			int ny=y+dir[i][1];
			if(in(nx,ny) && col[nx][ny]==0){
				if(mp[nx][ny]=='#')
				q.push({nx,ny});
				else mp2[x][y]='.';
			}
		}
	}
}
void work(){
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			if(mp[i][j]=='#' && col[i][j]==0){
				res++;
				bfs(i,j,res);
			}
		}
	}
}
void work2(){
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			if(col[i][j]!=0 && mp2[i][j]=='#')
			st.insert(col[i][j]);//去重
		}
	}
}
void solve(){
	printf("%d\n",res-st.size()); //开始的颜色就是连通块的个数
}
int main(){
	init();//初始化		
	work();//侵蚀前
	work2();//侵蚀后
	solve();//输出
	return 0;
}