合肥工业大学计算方法 实验三

1实验目的和要求

实验目的：
(1)熟悉非线性方程求根简单迭代法，牛顿迭代及牛顿下山法
(2)能编程实现简单迭代法，牛顿迭代及牛顿下山法
(3)认识选择迭代格式的重要性
(4)对迭代速度建立感性的认识；分析实验结果体会初值对迭代的影响

程序任务：
用牛顿下山法解方程（初值为0.6）
输入：初值，误差限，迭代最大次数，下山最大次数
输出：近似根各步下山因子

2实验环境和工具

用matlab或C语言实现

3实验结果

3.1算法流程图

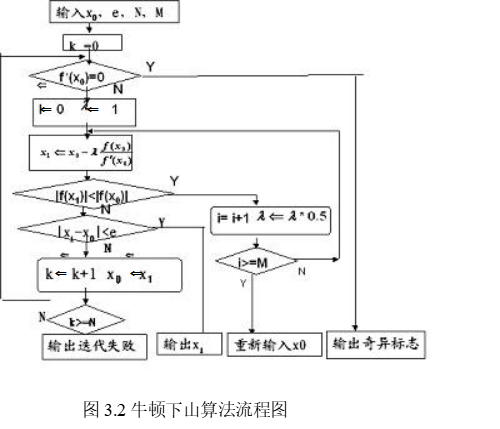
3.2程序核心代码

#include<stdio.h>
#include<math.h>

double f(double x)
{
    return x*x*x-x-1;
}

double ff(double x)
{
    return 3*x*x-1;
}

void newton(double x0,double e,int n,int m);
int main(void)
{
    double x0,e;
    int n,m;
    printf("输入：初值，误差限，迭代最大次数，下山最大次数\n\n");
    scanf("%lf %lf %d %d",&x0,&e,&n,&m);
    newton(x0,e,n,m);
    return 0;
}

void newton(double x0,double e,int n,int m)
{
    int k=0,i,is;
    double l,x1,ls;

    printf("近似跟\t下山因子\t迭代次数\t下山次数\n\n");
    while(k<n)
    {
        if(ff(x0)==0)
        {
            printf("奇异标志\n\n");
            return;
        }
        else
        {
            i = 0;
            l = 1;
ls = l;
is = i;

            while(1)
            {
                x1 = x0-l*f(x0)/ff(x0);
                if(fabs(f(x1))>fabs(f(x0)))
                {
                    i = i+1;
                    l = l*0.5;
                    if(i>=m)
                    {
                        printf("重新输入x0\n\n");
                        return;
                    }
                    printf("%lf\t%lf\t%d\t%d\n",x1,l,k,i);
                    ls = l;
                    is = i;
                }
                else
                {
                    break;
                }
            }

            if(fabs(x1-x0)<e)
            {
                printf("%lf\n\n",x1);
                return;
            }
            else
            {
                if(k>0)
                {
                    printf("%lf\t%lf\t%d\t%d\n",x1,ls,k,is);
                }
                k = k+1;
                x0 = x1;
            }
        }
    }
    printf("迭代失败\n\n");
    return;
}

3.3运行结果

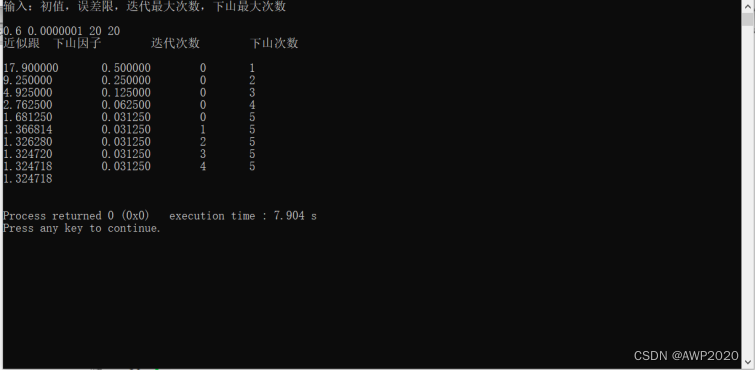
3.4运行结果分析
根据运行结果可得：
在迭代次数和下山次数内，即使是初值选取不当，最后也能得到符合要求的近似根，运用牛顿下山法，可以更便捷地获得方程的近似根。

4实验心得

思考题：
1.在实验1当最大下山比较大（如超过20）在x0=0.1及其附近将会产生什么结果？原因？
根据运行结果可得：
当下山次数较大且迭代次数较大（测试时使用的下山次数和迭代次数为100），取x0=0.1及其附近时，最终结果仍然为取x0=0.6时的近似根。
原因：
在进行测试的过程中，需要进行多次迭代和下山，在第一次下山完成后，进行多次迭代，然后进行第二次下山，多个过程以后，就可以得到想要的近似根。牛顿下山法的本质是将选取不当的初值变为合适的值，再进行迭代，如果迭代过程中发现值并不合适，就再次进行下山，重复过程，所以多次下山、迭代后，最终能得到符合要求的近似根。

2.如何将牛顿公式中的导数近似替换成差商并编程实现？
将导数的部分变为差商，第一步仍然使用导数，得到相应的x1，在后面，将所有的导数都变为(f(x1)-f(x0))/(x1-x0)，就是将牛顿公式中的导数近似替换成差商。

3.分析迭代收敛和发散的原因
迭代和发散的原因是对于初值的选择，只用牛顿迭代，如果初值和实际根相差太多，就会发散，如果相差较小，就会收敛。牛顿下山法的实质就是对初值进行处理，使之与实际根的差距减小，再用迭代求出近似根。
初值的选取极为重要，是影响迭代收敛和发散的原因。

心得：
在本次实验中，我复习了关于牛顿下山法的知识，牛顿下山法的效果好于牛顿迭代法。无论初值选取是否得当，在多次牛顿下山法后，都可以得到方程的近似根。
因为有老师给的算法流程图，所以编程并不是很困难。在本次实验中，遇到的最大困难是输出数据，最终经过多次检查后，发现是自己编程的过程中公式打错了。这也提醒我，算法固然重要，但是算法并不是好程序的唯一组成部分，有了好的算法，还要细心、仔细地去将算法实现，如果不够细心，纵然有好的算法，最后也难以给出好的程序。
在解决了自己粗心导致的错误后，程序就能正常运行了，也就能得到正常的结果了，这次实验，不仅让我回顾了牛顿下山法，同时也警醒我，除了算法之外，程序的其他组成部分也是至关重要的，水桶所能装的水取绝于最短的木板，一个程序员的水平也和他最薄弱的方面相关。
经过本次实验，我要继续努力，补足自己的每一个短板，在以后要更加细心，为成为一个合格的程序员不断努力。