用Python分析资产收益的典型化事实
什么是典型化事实?
Wiki上对于stylized fact是这么定义的:
In social sciences, especially economics, a stylized fact is a simplified presentation of an empirical finding. A stylized fact is often a broad generalization that summarizes some complicated statistical calculations, which although essentially true may have inaccuracies in the detail.
首先,典型化事实是在实际数据中发现的一些现象。然而简单的从一些数据中得到的“结论”并不能就称之为“典型化事实”,一个典型化的事实应该是怎数据中比较稳健的,虽然在某些特例中,这些典型化事实并非总是成立。
为什么需要典型化事实?因为这些是经济学理论需要解释的现象,同时这些事实可以反过来检验经济学的理论是否能解释这个领域的现象。
典型化事实在这里有两方面的作用:指出了之前理论的缺陷;为新的理论指明了方向。
那么 为什么“典型化事实”可能不是“事实”,有两个方面的原因。首先,“典型化事实”通常只是一个统计上的描述,远非事实本身。
举一个是wiki上的例子:A prominent example of a stylized fact is: "Education significantly raises lifetime income."教育提升了生命周期的收入。如果只看这句话,多数人会有一个印象,也就是“接受教育提高了收入”,这似乎是一个因果关系。然而这个因果关系成立么?典型化的事实并不能告诉我们这个答案。
经典的劳动经济学通常会告诉你,一个人接受教育可能是因为他的能力比较高,而能力高的人可能就算不接受更高程度的教育也可以达到同样的收入。是不是接受更高程度的教育,比如是否读博,本身就是一个根据自身能力选择的结果,从“反事实”的角度来讲,以上的“事实”并不严格构成因果关系。我想如果我当时没有选择读博,而是直接工作,薪水待遇会比我读博毕业之后更高吧。
总结下来,“典型化事实”在经济学中非常重要,无论是宏观经济学还是贸易、金融还是产业经济学,在理论的发展中都扮演着非常重要的角色,因而如果能发现一些“典型化事实”,对经济学的理论研究和之后的实证研究是非常重要的。然而,作为非科研人员,则要警惕过度解读“典型化事实”。基于以上的两点原因,即使有了这些“典型化事实”,我们仍然需要理论和逻辑进行判断。
典型化事实(Stylized Facts)是出现在许多资产回报(跨时间和市场)中的统计属性。了解它们很重要,因为当我们构建代表资产价格动态的模型时,模型必须能够捕获这些属性。
分析案例
我们使用从 1985 年到 2018 年标普 500 指数的每日回报收益来分析五个典型化事实。从雅虎财经下载标准普尔 500 指数价格并计算收益。使用以下代码导入所有需要的库:
import pandas as pd
import numpy as np
import yfinance as yf
import seaborn as sns
import scipy.stats as scs
import statsmodels.api as sm
import statsmodels.tsa.api as smt
import matplotlib.pyplot as plt
本文中,我们将用 Python去发现标准普尔 500 指数系列中的五个典型化事实。
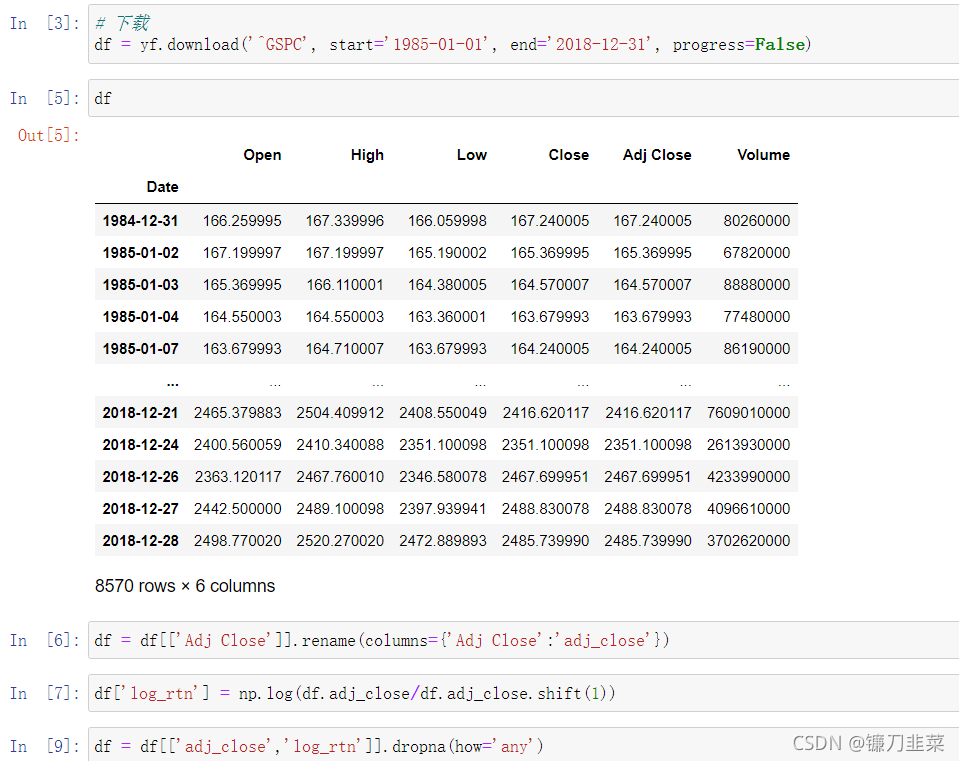
1. 资产收益的非高斯分布
执行以下代码,绘制收益直方图和Q-Q图来发现第一个事实的存在。
1.1 使用观察到的收益的均值和标准差计算正态概率密度函数(PDF):
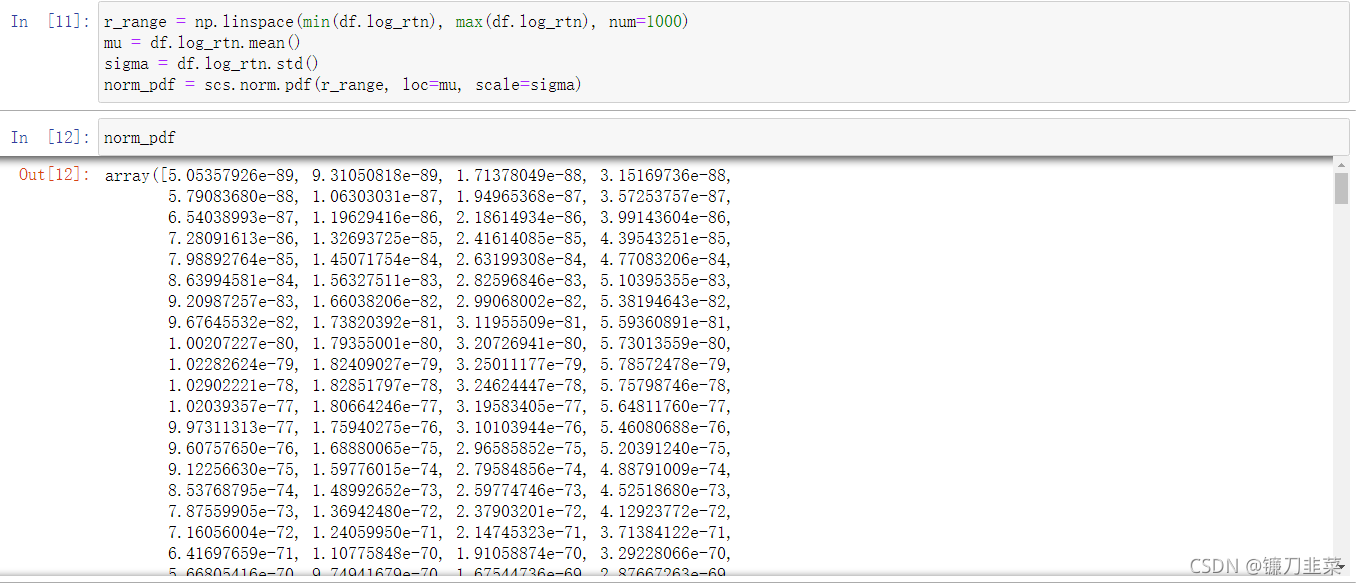
1.2 绘制直方图和Q-Q图
fig, ax = plt.subplots(1, 2, figsize=(16, 8))
# histogram
sns.distplot(df.log_rtn, kde=False, norm_hist=True, ax=ax[0])
ax[0].set_title('Distribution of S&P 500 returns', fontsize=16)
ax[0].plot(r_range, norm_pdf, 'g', lw=2,
label=f'N({mu:.2f}, {sigma**2:.4f})')
ax[0].legend(loc='upper left');
# Q-Q plot
qq = sm.qqplot(df.log_rtn.values, line='s', ax=ax[1])
ax[1].set_title('Q-Q plot', fontsize = 16)
# plt.tight_layout()
# plt.savefig('images/ch1_im10.png')
plt.show()
执行上面的代码产生如下直方图和Q-Q图:
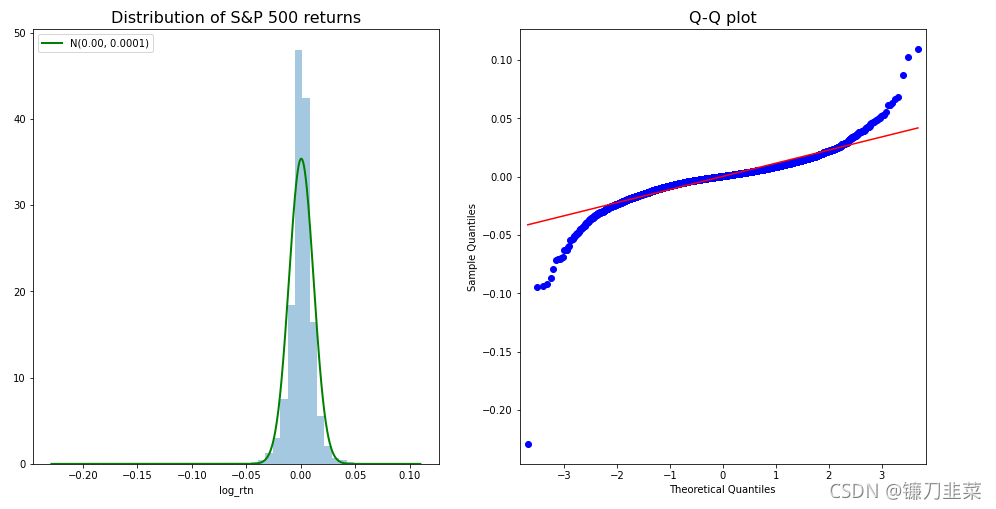
我们可以使用直方图(显示分布的形状)和 Q-Q 图来评估收益的正态性。
2. 波动集聚性
运行以下代码,通过绘制收益序列来发现第二个典型化事实。
2.1 可视化收益序列:
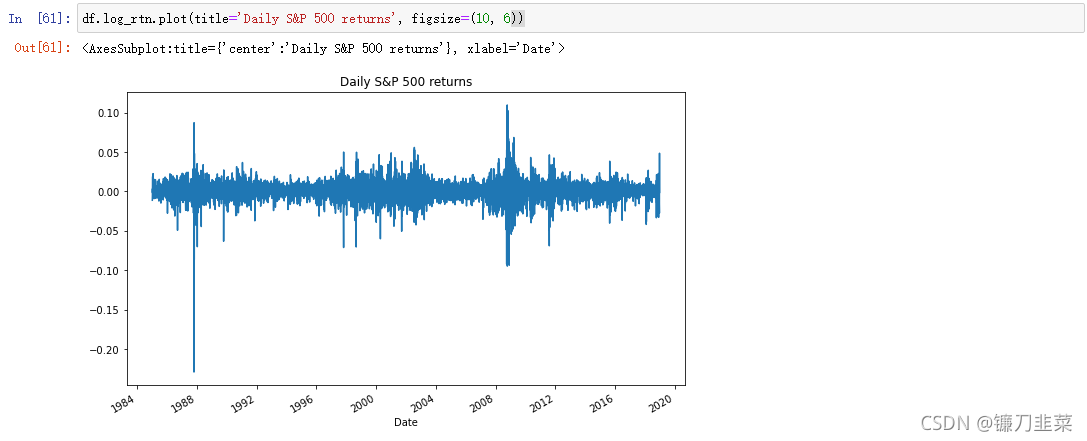
可以观察到明显的波动集聚性——波动较大的正收益和负收益时期。
3. 收益不存在自相关性
继续去发现第三个典型化事实。
3.1 定义用于创建自相关图的参数
N_LAGS = 50
SIGNIFICANCE_LEVEL = 0.05
3.2 运行以下代码以创建收益的自相关函数(ACF)图:
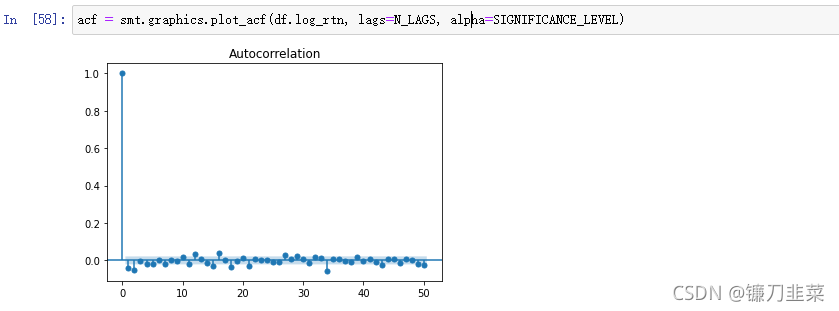
只有少数值位于置信区间之外并且可以被认为具有统计显著性。我们可以假设已经验证了收益序列中没有自相关性。
4. 平方/绝对收益的自相关性小且递减
通过创建平方和绝对收益的 ACF 图来研究第四个典型化事实。
4.1 创建ACF图
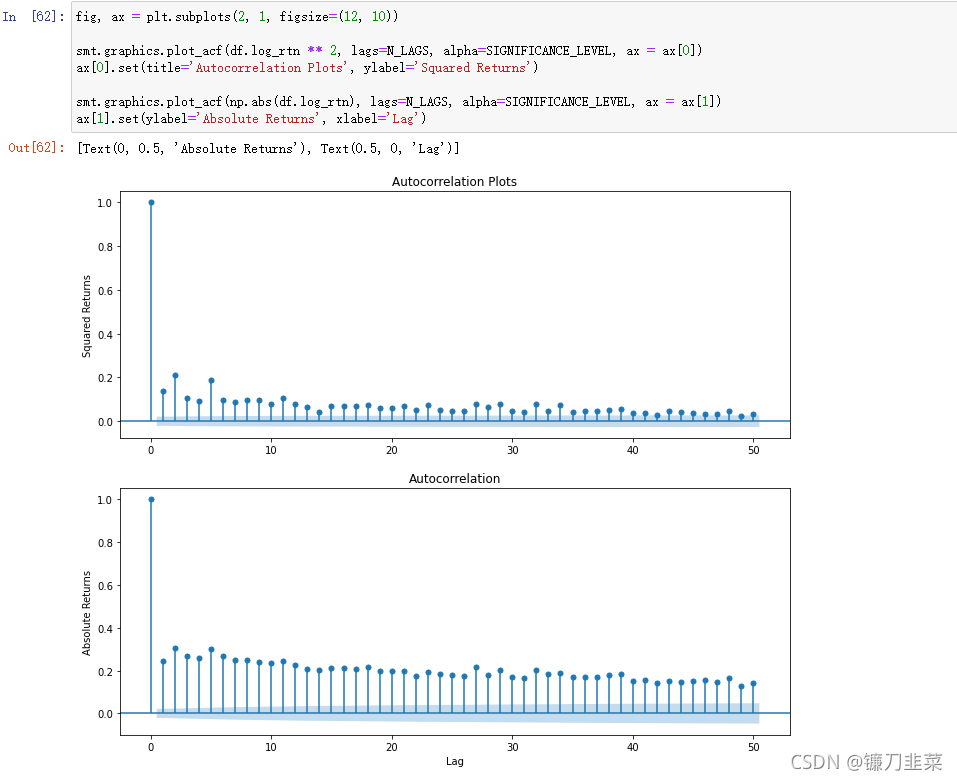
可以观察到平方回报和绝对回报的自相关值很小且不断减小,这与第四种典型化事实一致。
5. 杠杆效应
运行以下步骤来调查杠杆效应的存在。
5.1 将波动性度量计算为滚动标准偏差:
df['moving_std_252'] = df[['log_rtn']].rolling(window=252).std()
df['moving_std_21'] = df[['log_rtn']].rolling(window=21).std()
5.2 绘制所有系列以进行比较
fig, ax = plt.subplots(3, 1, figsize=(18, 15), sharex=True)
df.adj_close.plot(ax=ax[0])
ax[0].set(title='S&P 500 time series', ylabel='Price ($)')
df.log_rtn.plot(ax=ax[1])
ax[1].set(ylabel='Log returns (%)')
df.moving_std_252.plot(ax=ax[2], color='r', label='Moving Volatility 252d')
df.moving_std_21.plot(ax=ax[2], color='g', label='Moving Volatility 21d')
ax[2].set(ylabel='Moving Volatility', xlabel='Date')
ax[2].legend()
现在可以通过将价格序列与(滚动)波动率指标进行可视化比较来研究杠杆效应:
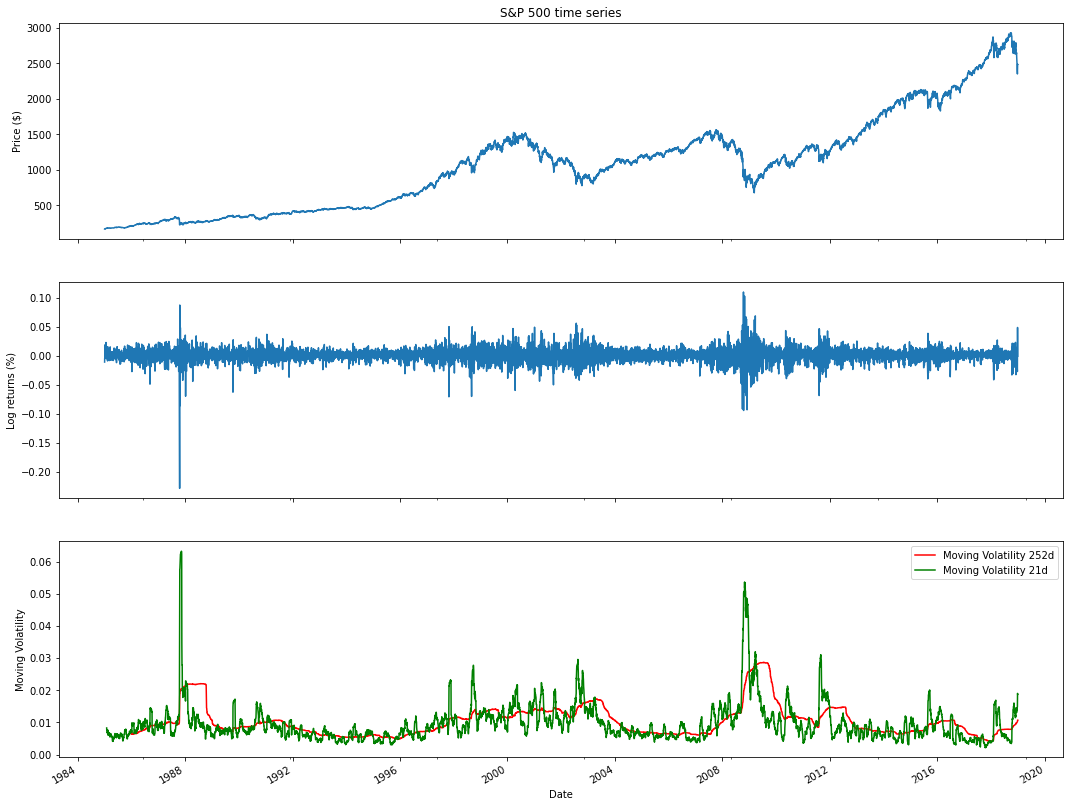
这一事实表明,资产波动性的大多数衡量标准与其回报呈负相关,我们确实可以观察到价格下跌时波动性增加而价格上涨时波动性减少的模式。
Jarque-Bera test
1. Jarque-Bera 检验数学公式:
The Jarque-Bera test is a goodness-of-fit test that determines whether or not sample data have skewness and kurtosis that matches a normal distribution.
意思是说,Jarque-Bera检验的目的是通过偏度(skewness)和峰度来检验样本是否来自正态分布,正态分布的偏度为0,峰度为3。
当样本服从正态分布时,JB统计量为:
J
B
=
n
(
S
2
6
+
(
K
−
3
)
2
24
)
JB = n(\frac{S^2}{6}+\frac{(K-3)^2}{24})
JB=n(6S2+24(K−3)2)
渐近服从
χ
2
(
2
)
\chi ^2(2)
χ2(2)。其中n为样本规模,S、K分别为随机变量的偏度和峰度,计算公式如下:
M
2
=
∑
i
(
x
i
−
x
ˉ
)
2
n
M2=\frac{\sum_{i}^{}(x_i-\bar{x})^2}{n}
M2=n∑i(xi−xˉ)2
S
=
∑
i
(
x
i
−
x
ˉ
)
3
n
M
2
1.5
S=\frac{\frac{\sum_{i}^{}(x_i-\bar{x})^3}{n}}{M2^{1.5}}
S=M21.5n∑i(xi−xˉ)3
K
=
∑
i
(
x
i
−
x
ˉ
)
4
n
M
2
2
K=\frac{\frac{\sum_{i}^{}(x_i-\bar{x})^4}{n}}{M2^2}
K=M22n∑i(xi−xˉ)4
python的sicipy.stats中偏度和峰度的调用的函数为stats.skew(y)、stats.kurtosis(y),其中峰度的公式为:
K
=
∑
i
(
x
i
−
x
ˉ
)
4
n
M
2
2
−
3
K=\frac{\frac{\sum_{i}^{}(x_i-\bar{x})^4}{n}}{M2^2}-3
K=M22n∑i(xi−xˉ)4−3
2. Jarque-Bera 检验代码
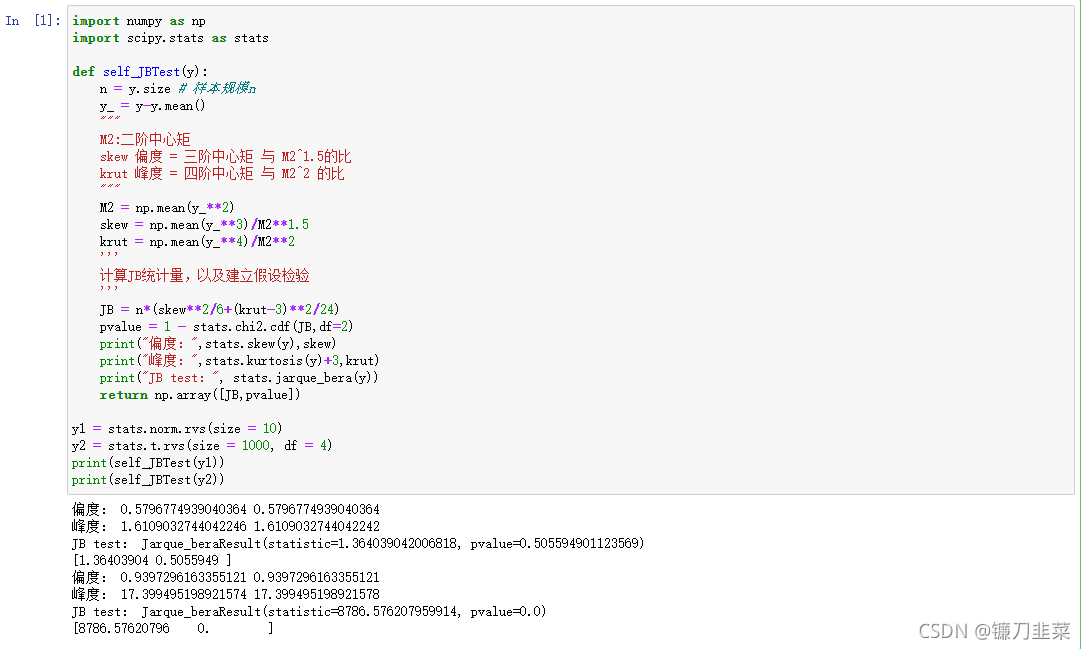
3.什么时候使用 Jarque-Bera 测试
Jarque-Bera 检验通常用于其他正态性检验(如 Shapiro-Wilk 检验)不可靠的大型数据集(n > 2000)。
这是在执行一些假设数据集服从正态分布的分析之前使用的适当测试。 Jarque-Bera 检验可以告诉您是否满足此假设。
参考资料
[1] https://www.zhihu.com/question/31699378 慧航
[2] https://www.statology.org/jarque-bera-test-python/





 本文通过Python分析标准普尔500指数的收益,揭示了资产收益的非高斯分布、波动集聚性、自相关性、平方/绝对收益的自相关性和杠杆效应等五个典型化事实。使用直方图、Q-Q图、自相关函数图等可视化工具,以及Jarque-Bera检验来评估数据特性。这些发现对于理解金融市场动态和构建资产价格模型至关重要。
本文通过Python分析标准普尔500指数的收益,揭示了资产收益的非高斯分布、波动集聚性、自相关性、平方/绝对收益的自相关性和杠杆效应等五个典型化事实。使用直方图、Q-Q图、自相关函数图等可视化工具,以及Jarque-Bera检验来评估数据特性。这些发现对于理解金融市场动态和构建资产价格模型至关重要。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










