二叉树以及前、中、后序遍历

最新推荐文章于 2024-02-28 11:47:37 发布

原创最新推荐文章于 2024-02-28 11:47:37 发布 · 266 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#二叉树 #数据结构

数据结构与算法专栏收录该内容

34 篇文章

订阅专栏

本文深入探讨了二叉树的前序、中序和后序遍历方法，通过具体的代码实现展示了如何构建和遍历一棵二叉树，是理解二叉树结构和遍历算法的实用指南。

二叉树

树的结构

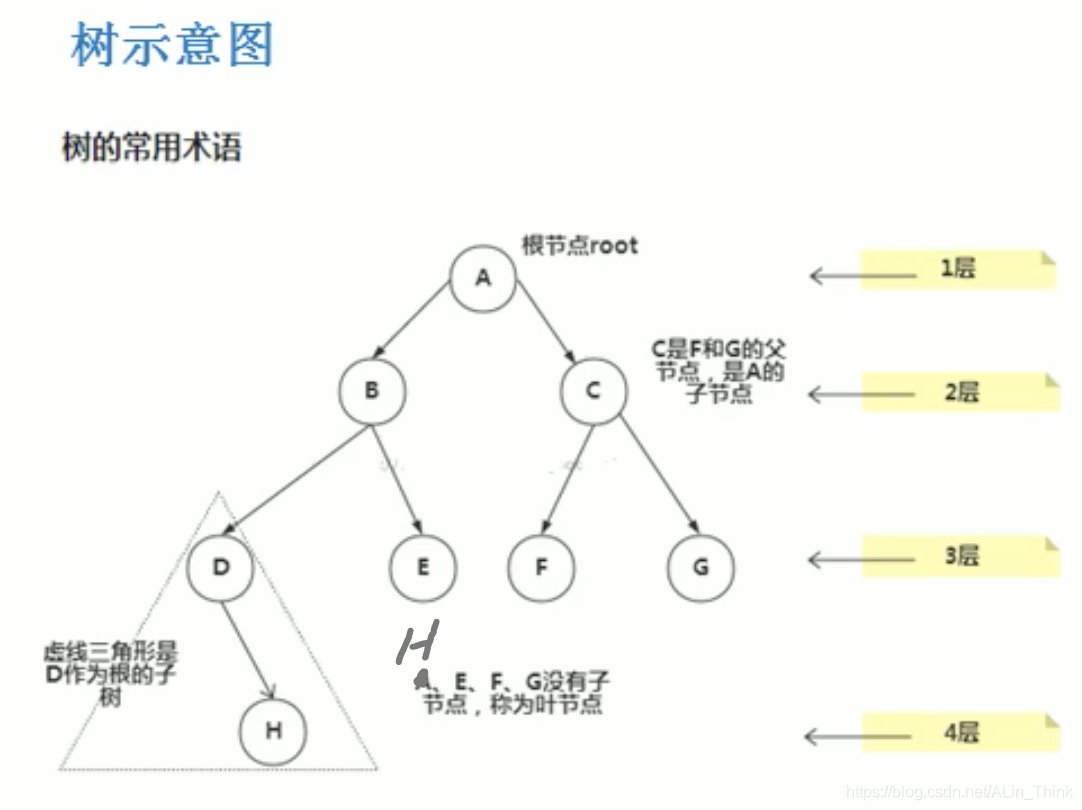
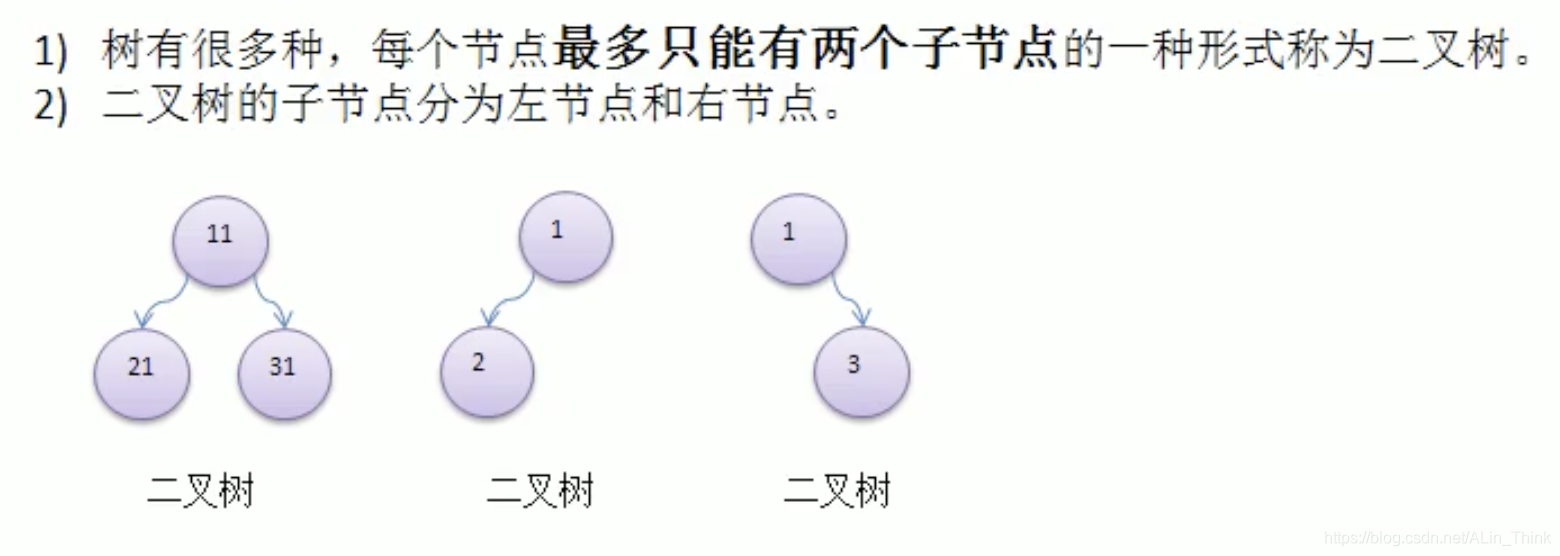
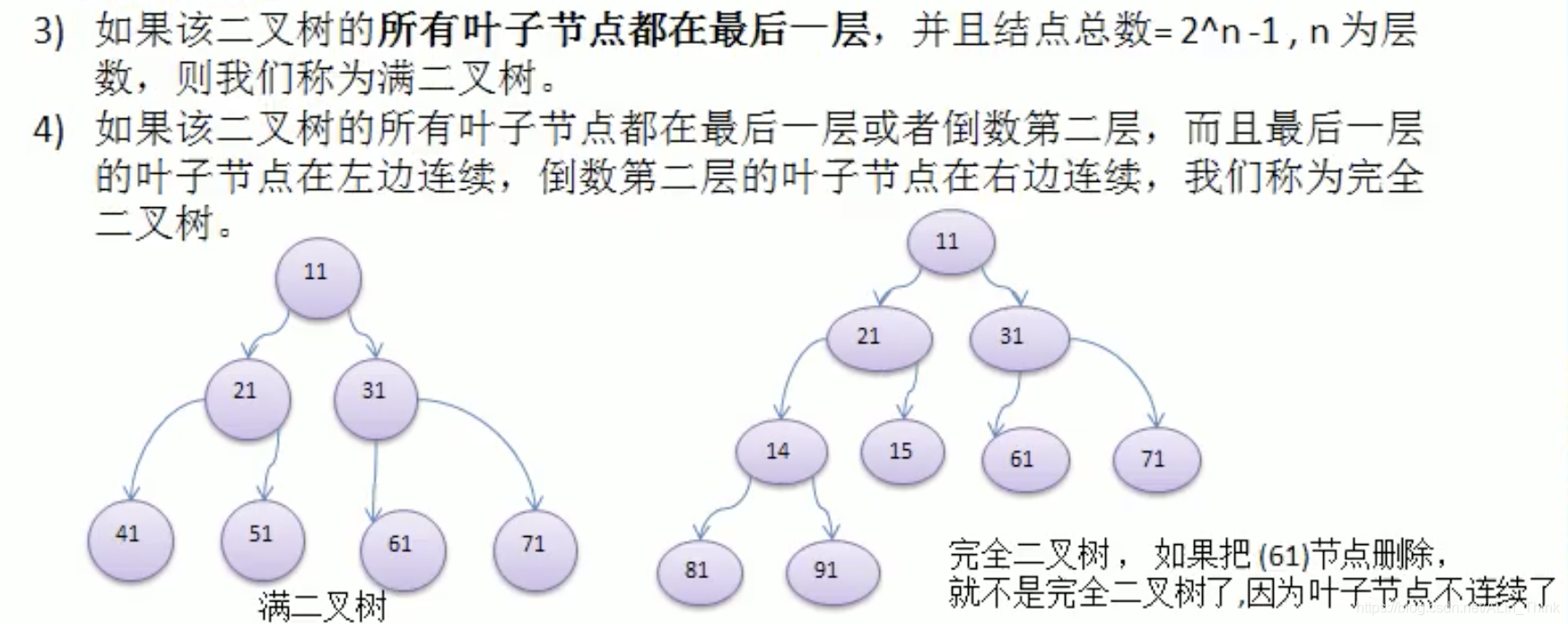
在这里插入图片描述

二叉树的概念

在这里插入图片描述

前序、中序、后序遍历

前序：先输出根节点，在遍历左子树，在遍历右子树
中序：先遍历左子树，在输出根节点，在遍历右子树
后序：先遍历历左子树，在遍历右子树，在输出根节点

代码

package tree;

public class BinaryTreeDemo {
    public static void main(String[] args) {
        // 创建一个空二叉树
        BinaryTree binaryTree = new BinaryTree();
        // 创建节点
        HeroNode root = new HeroNode(1,"皮卡丘");
        HeroNode node2 = new HeroNode(2,"杰尼龟");
        HeroNode node3 = new HeroNode(3,"小火龙");
        HeroNode node4 = new HeroNode(4,"妙蛙种子");
        // 挂载构建二叉数
        binaryTree.setRoot(root);
        root.setLeft(node2);
        root.setRight(node3);
        node3.setRight(node4);

        binaryTree.postOrder();
    }
}
class BinaryTree{
    private HeroNode root;

    public void setRoot(HeroNode root) {
        this.root = root;
    }

    // 前序
    public void preOrder(){
        if (this.root != null){
            this.root.preOrder();
        } else {
            System.out.println("null");
        }
    }
    // 中序
    public void infixOrder(){
        if (this.root != null){
            this.root.infixOrder();
        } else {
            System.out.println("null");
        }
    }
    // 后序
    public void postOrder(){
        if (this.root != null){
            this.root.postOrder();
        } else {
            System.out.println("null");
        }
    }
}
class HeroNode {
    private int id;
    private String name;
    private HeroNode left;
    private HeroNode right;

    public HeroNode(int id, String name) {
        this.id = id;
        this.name = name;
    }

    public int getId() {
        return id;
    }

    public void setId(int id) {
        this.id = id;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public HeroNode getLeft() {
        return left;
    }

    public void setLeft(HeroNode left) {
        this.left = left;
    }

    public HeroNode getRight() {
        return right;
    }

    public void setRight(HeroNode right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "HeroNode{" +
                "id=" + id +
                ", name='" + name + '\'' +
                '}';
    }

    // 前序
    public void preOrder() {
        System.out.println(this);
        if (this.left != null) {
            this.left.preOrder();
        }
        if (this.right != null) {
            this.right.preOrder();
        }
    }

    // 中序
    public void infixOrder() {
        if (this.left != null) {
            this.left.infixOrder();
        }
        System.out.println(this);
        if (this.right != null) {
            this.right.infixOrder();
        }
    }
    // 后序
    public void postOrder() {
        if (this.left != null) {
            this.left.postOrder();
        }
        if (this.right != null) {
            this.right.postOrder();
        }
        System.out.println(this);
    }
}