手动分解反向传播，理解梯度消失和梯度爆炸_梯度反向传播和梯度截断-优快云博客

博客围绕深度学习中梯度的手写公式推导展开，分析了各层变量梯度的计算方式，指出训练变量、激活函数导数和激活值影响梯度。还阐述了梯度爆炸和消失的条件，并从训练变量、激活函数导数、激活值和模型结构四个方面给出防止梯度异常的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

来自博客

Let’s see a very simple handwriting formula derivation

Define

Firstly, let define some variables and operations
在这里插入图片描述

Gradient of the variable in layer L(last layer)

dWL = dLoss * aL
在这里插入图片描述

Gradient of the variable in layer L-1

dW(L-1) = dLoss * WL * dF(L-1) * a(L-1)
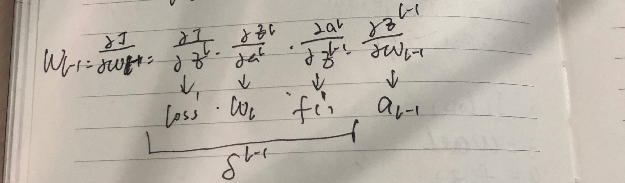
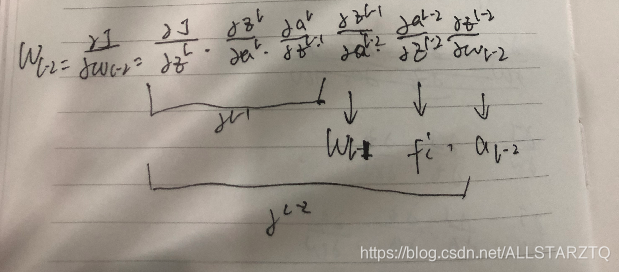
在这里插入图片描述

Gradient of the variable in layer L-2

dW(L-2) = dLoss * WL * dF(L-1) * a(L-1) * W(L-1) * dF(L-2) * a(L-2)
在这里插入图片描述

Summary

So, as we can see, the gradient of any training variables only depends on the variable itself(W), the derivative of activation function(dF), and the activated value(a).

Relations with gradient vanishing or exploding

Gradient exploding

Training variables are larger than 1, or the derivative of activation function are larger than 1, or the nd the activated value are larger than 1.

Gradient vanishing

Training variables are smaller than 1, or the derivative of activation function are smaller than 1, or the nd the activated value are smaller than 1.

To prevent graident vanishing or exploding

From the view of training variables

To limit the traning variables into a proper range. We shoudl use a good variable initialization technic, such as xavier initialization.

From the view of derivative of activation function

To limit derivative of activation function to a proper range, we should use non-saturated activation function as activation instead of sigmoid

From the view of activated value

To limit the activation value in to proper range, we should use batchnorm to make the activated value into a zero centered and variance to one.

From the view of model structure

To future enhance the gradient to the shallow layer, we should use residual block to construct our network.