一文读懂监督学习中分类算法5种评估指标、回归算法6种评估指标的奥秘

对于监督学习训练得到的模型，到底如何评价一个模型预测的好坏呢？不同模型预测的结果如何比较？一般可以使用评估指标来进行模型评价和比较。评估指标有两个作用：

了解模型的泛化能力，可以通过同一个评估指标来对比不同模型，从而知道哪个模型相对较好，哪个模型相对较差。

可以通过评估指标来逐步优化模型，而评估方法提供了不同情景下使用这些指标对模型进行评价。

用于模型评价的评估指标有很多，按照类别可以分为：

适用于分类模型：混淆矩阵、准确率、查准率、查全率、F1、ROC曲线等。

适用于回归模型：MSE、RMSE、MAE、MAPE、R-Square、Adjust R-Square等。

1.分类算法的评估指标

分类模型常用的几个评估指标都是基于混淆矩阵构建。混淆矩阵如表6-1所示。

☀什么是混淆矩阵？

1.基本概念 混淆矩阵就像是一个成绩报告单，不过这个报告单是用来评估一个预测模型（比如预测明天会不会下雨、预测一个图片是猫还是狗之类的模型）的表现怎么样的。 2.具体解释 假设我们有一个模型是用来判断一个动物是猫还是狗。这个混淆矩阵就像是一个表格，有两行两列（如果是更复杂的分类，行列会更多）。 表格的行代表的是实际情况，比如第一行是“实际是猫”，第二行是“实际是狗”。列代表的是模型的预测结果，第一列是“预测是猫”，第二列是“预测是狗”。 当一个动物实际上是猫，模型也预测是猫，这个情况就记录在第一行第一列的格子里，这个数字就表示有多少个动物是这种情况，称为真正例。如果实际是猫，但是模型预测是狗，就记录在第一行第二列的格子里，称为假正例。同样的，实际是狗，预测是猫记录在第二行第一列，称为假反例，实际是狗，预测也是狗记录在第二行第二列，称为真反例。 3.用途举例 通过这个表格，我们可以很清楚地看到模型在预测的时候哪里做对了，哪里做错了。比如第一行第一列和第二行第二列的数字加起来，就是模型预测正确的次数。而其他两个格子里的数字加起来，就是模型预测错误的次数。这样我们就能直观地评估这个模型的准确性，就像通过成绩报告单看学生的成绩一样。

真正例，真反例，都为真，表示预测正确，这儿的正表示猫，反表示狗；假正例，假反例，都为假，表示预测错误。

（1）准确率 (Accuracy) 

准确率是一个描述模型总体准确情况的百分比指标，主要用来说明模型的总体预测准确情况，计算公式如下：

准确率=（真正例+真反例）/N

准确率虽然可以判断总体的正确率，不过，当数据类别不平衡的时候，准确率可能会 “骗人”。比如说，你要预测一种很罕见的疾病，只有 1% 的人患有这种病。如果你的模型总是预测没有病，那么准确率可能会很高，但实际上这个模型可能没什么用，因为它没有正确地识别出真正患病的人。

（2）查准率(Precision)

对于预测问题来说，往往关注的并不是模型的准确率。比如，你有一个模型用来预测图片是猫还是狗，查准率（以猫为例）就是在所有模型预测为猫的图片中，真正是猫的图片所占的比例。它主要关注的是预测为正类（比如预测是猫）的准确性，而不是整体的预测准确性。

查准率=真正例/（真正例+假正例）

（3）查全率(Recall)

只是查准率高似乎也有问题查全率也是针对某一特定类别的。对于猫这个类别，查全率是指在所有真正是猫的图片中，被模型正确预测为猫的图片所占的比例。因此就需要使用查全率，查全率也称召回率或命中率，主要是反映正例的覆盖程度，它是实际为正例的样本中被正确预测为正例的样本所占的比例，计算公式如下：

查全率=真正例 /（真正例+假反例）

☀查准率和查全率的区别？

查全率：侧重于衡量模型能够把某一类别全部找出来的能力。它是从 “全面性” 的角度出发，关注的是有没有遗漏该类别的样本。 查准率：主要关注的是模型预测为某一类别时的准确性。它是从 “准确性”的角度来评估，重点是模型预测为这个类别时，有多少是真正属于这个类别的。

☀查全率和查准率之间具有互逆的关系，当查准率高的时候，查全率一般很低；查全率高时，查准率一般很低，该如何理解这句话？

1.查准率高、查全率低的情况 想象一个模型像一个很“挑剔”的选猫器。为了保证选出的肯定是猫（高查准率），标准设得很严。这样一来，有些不太典型的猫（比如猫的样子不明显）就会被漏选，所以查全率就低了。 2.查全率高、查准率低的情况 要是模型是个很“宽松”的选猫器，只要有点像猫就选进来。这样虽然几乎所有猫都能被选到（高查全率），但也会把很多不是猫的东西选进来，查准率就低了。

（4）F1值

由于查全率和查准率之间互逆的关系，使用单一指标会导致一定的片面性，因此可以使用查准率和查全率的调和平均值来评估模型性能，计算公式如下：

F1=2×查全率×查准率/（查全率+查准率）

☀大家有没有想过，F1值的公式为什么这么设计？

分子设计：分子采用查全率和查准率的乘积再乘以2，是为了强调查全率和查准率的同时重要性。当查全率和查准率都比较高时，它们的乘积就会比较大，从而使F1值也比较高。乘以2这个系数是为了方便计算和理解，它没有改变指标对查全率和查准率平衡考虑的本质。 分母设计：分母采用查全率和查准率的和，是为了起到一种平衡和归一化的作用。这样设计可以防止F1值被某个过高的指标单方面拉高。 比如，如果只考虑乘积，可能会出现一种情况：一个指标非常高，另一个指标很低，但乘积仍然可能看起来不错。以查全率为0.1，查准率为0.9为例，乘积为0.09，看起来不是很差。但如果我们考虑F1值的完整公式，分母为 0.1 + 0.9 = 1，分子为 2×0.1×0.9 =0.18，F1值为0.18，这样就能更合理地反映出这个模型实际上在两个指标平衡上的不佳表现。

（5）ROC曲线（Receiver Operating Characteristic Curve）

它就像是一个 “性能评估图”，主要用于评估一个二分类模型（比如判断一个东西是真还是假、有病还是没病）的好坏。这个曲线是通过不断改变模型的决策阈值来绘制的。

我们要通过改变判断的阈值来绘制ROC曲线。比如说，最初我们设定阈值为0.5，即模型输出的概率大于0.5就判定为猫，小于0.5就判定为狗。

☛真阳性率（TPR）：假如数据集中有100张猫的图片。当阈值为 0.5时，模型正确判断为猫的图片有80 张，那么真阳性率（TPR） =正确判断为猫的猫图片数÷总猫图片数=80÷100=0.8。这就像是在一堆真正的宝藏（猫图片）中，我们正确找到的宝藏比例。

☛假阳性率（FPR）：假设数据集中有100张狗的图片。当阈值为0.5 时，模型错误地把30张狗的图片判断为猫，那么假阳性率（FPR） =错误判断为猫的狗图片数÷总狗图片数=30÷100=0.3。这好比在一堆普通石头（狗图片）中，我们错误地把石头当作宝藏（猫）的比例。

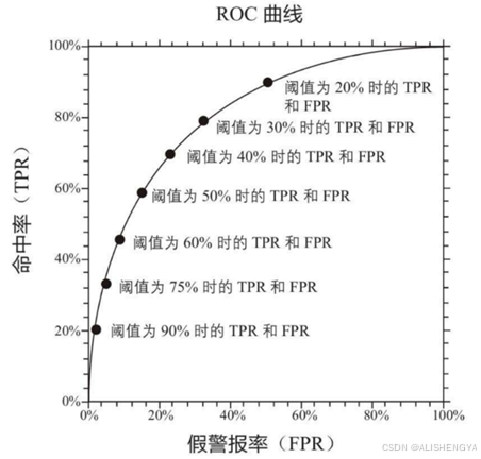
我们以假阳性率（FPR）为横轴，真阳性率（TPR）为纵轴来绘制 ROC曲线。当我们降低阈值，比如设为0.3，模型会更容易把图片判断为猫。这样一来，真阳性率（TPR）可能会升高，因为更多的猫图片会被正确判断为猫，但同时假阳性率（FPR）也可能会升高，因为会有更多的狗图片被误判为猫。

2.回归模型的评估指标

（1）均方误差（MSE）

是一种衡量预测值与真实值之间差异的指标。它主要用于评估回归模型的性能，也就是模型在预测数值（比如预测房价、温度等）方面的好坏。

计算方式是先求出每个预测值与真实值的差，将这个差平方（这样做是为了避免正负差相互抵消，并且放大误差），然后求这些平方差的平均值。

假设目标变量的真实值为yi，预测值为fi，下面几个指标常用来评估回归模型的优劣。

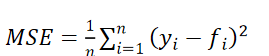
MSE的值越小，说明预测值和真实值越接近，模型的性能就越好。

（2）RMSE(Root Mean Square Error)  均方根误差，在MSE的基础上开平方根。

如果说MSE衡量的是预测值与真实值偏差的平方的平均水平，RMSE 则是将这个平均平方误差还原到和原始数据相同的量纲，让我们能更直观地理解预测误差的大小。

在模型比较和选择中，RMSE是一个重要的指标，我们通常希望选择RMSE较小的模型，因为这意味着模型预测的准确性更高。

（3）MAE（Mean Absolute Error） 平均绝对误差

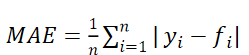
是基于预测值和真实值之间差值的绝对值，相较于均方误差（MSE），MAE更直观地反映了预测误差的实际平均大小。

与MSE相比，MAE对异常值（离群点）不太敏感。因为它只计算差值的绝对值，而不是像MSE那样对差值进行平方，所以异常值不会过度影响MAE的值。这使得MAE在数据可能存在异常值的情况下，能更稳健地评估模型性能。

（4）MAPE (Mean Absolute Percentage Error)

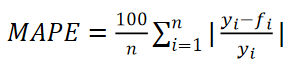
MAPE（平均绝对百分比误差）是一种衡量预测准确性的指标，用于评估预测值与真实值之间的相对误差。它通过计算预测值与真实值之间差异的绝对值占真实值的百分比的平均值，来反映预测的精度。这种相对误差的衡量方式使得MAPE在比较不同规模数据集或不同量级变量的预测准确性时非常有用。

（5）R-square(决定系数)

R-square（决定系数），也称为判定系数，是用于衡量回归模型拟合优度的一个重要指标。它表示因变量（被预测变量）的变异中可以由自变量（用于预测的变量）解释的比例。其取值范围在0到1之间，越接近1，表示模型对数据的拟合程度越好；越接近0，表示模型拟合得越差。

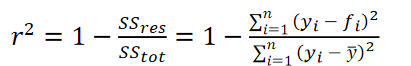
在数据分析中，用于比较不同回归模型对同一数据集的拟合效果，选择拟合程度更好的模型。

R-square会随着自变量的增加而增大，即使新增加的自变量对因变量没有实际的解释力。这可能导致过度拟合的模型看起来拟合程度很好。因此，在使用R-square时，需要结合其他指标（如调整后的R-square）和实际情况来综合评估模型的质量。

（6）Adjusted R-Square (校正决定系数）

Adjusted R-Square（校正决定系数）是对R-Square（决定系数）的一种修正。我们知道，R-Square会随着模型中自变量数量的增加而增大，即使新增加的自变量对因变量并没有实际的解释力。这就可能导致一种情况，我们仅仅通过不断添加无关的自变量来使R-Square看起来很好，产生过度拟合的问题。为了避免这种虚假的拟合优度提升，就引入了Adjusted R-Square。

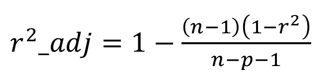
其中是样本数量，是自变量的数量，是决定系数。当我们需要比较不同自变量组合的回归模型，或者评估添加新的自变量是否真正提高了模型的拟合质量时，Adjusted R-Square是一个非常有用的指标。