该公式可以理解为将曲线划分为若干个梯形,数量越多,结果越精确。
这个程序实现有点太过于基础,这里就不一一叙述,直接上代码。不过要改变积分函数的话就调用函数改为新的函数即可。
void func(int n)//调用求f(xi)的函数
{
for (int i = 0; i <= n; i++)
{
f[i] = 8 + x[i] * x[i] * x[i];
}
}
附上实现程序(Visual Studio 2019)
#include <iostream>
#include <iomanip>//保留小数
double x[100];//定义节点的x坐标
double f[100];//定义节点的函数值f
double h;//定义步长
void func(int n);//调用求f(xi)的函数
double i_f;//定义复合梯形求解结果
double func_i_f(int n);//调用复合梯形求积函数
int main()
{
using namespace std;
int n;
cout << "输入等分数" << endl;
cin >> n;
cout << "输入x的上限值" << endl;
cin >> x[n];
cout << "输入x的下限值" << endl;
cin >> x[0];//赋值模块
h = (x[n] - x[0]) / n;//求步长h
for (int i = 1; i <= n - 1; i++)
{
x[i] = x[0] + i * h;
}//求每个节点x坐标值
func(n);
func_i_f(n);
cout << setiosflags(ios::fixed) << setprecision(5);//输出结果保留5位小数
cout << "f(x)=8 + x^3在x区间上的积分值为:" ;
cout << i_f << endl;
return 0;
}
void func(int n)//调用求f(xi)的函数
{
for (int i = 0; i <= n; i++)
{
f[i] = 8 + x[i] * x[i] * x[i];
}
}
double func_i_f(int n)//调用复合梯形求积函数
{
i_f = 0;
for (int i = 0; i <= n - 1; i++)
{
i_f += (f[i] + f[i + 1]) * h / 2;
}
return i_f;
}
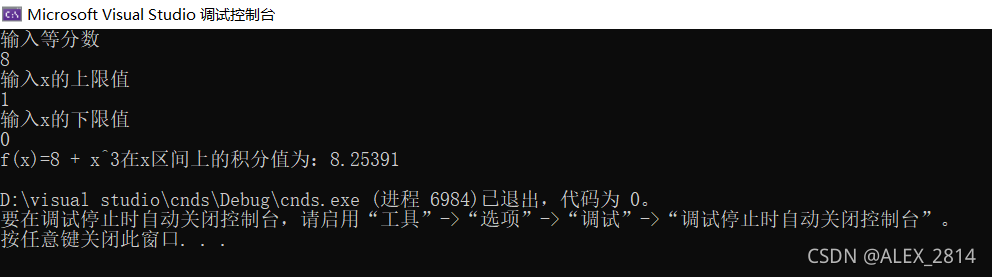
结果输出
后话
关于《数值分析》与C++联动小项目就到这里结束了!接下来的一个小小工作就把高斯迭代那一篇的程序推向n阶。





 本文通过一个C++程序展示了如何利用复合梯形法则进行数值积分,通过不断细分梯形来提高计算精度。用户可以输入等分数及积分区间,程序会输出相应结果,适用于基础的数值分析教学与实践。
本文通过一个C++程序展示了如何利用复合梯形法则进行数值积分,通过不断细分梯形来提高计算精度。用户可以输入等分数及积分区间,程序会输出相应结果,适用于基础的数值分析教学与实践。
















 8911
8911

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








