支持向量机（SVM）的推导

目录

一、什么是支持向量机（svm）

二、推导过程

三、svm的优缺点：

优点：

缺点：

---

一、什么是支持向量机（svm）

支持向量机（Support Vector Machine, SVM）是一种常用的监督学习算法，主要用于二分类问题，但也可以扩展到多分类问题。它可以通过在特征空间中找到一个最优的超平面来进行分类，同时最大化超平面与最近的数据点之间的间隔。

二、推导过程

现在这里有这么一堆点：我们要想办法用一条线把它们分隔开，使线的一边是蓝色点，另一边是绿色点，线该怎么划呢？

我们可以这样随意的画出几条这样的线来：

但是，这些线看起来都离点的距离太近了，划分的效果不是很明显，例如：如果我们现在增加这样一个绿点，它就会被划分到线的另一边去，被视为蓝点一类了，可是根据我们的直观感受，这个新增的绿点应该属于下面这一大群绿点一类。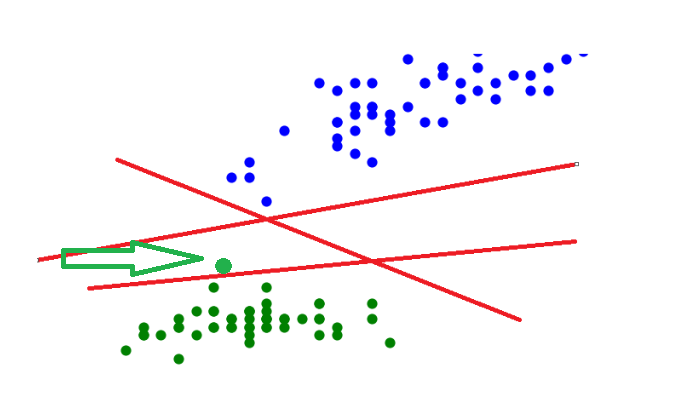

所以我们现在需要想象画出这样一条线：它能将两类数据正确划分并且间隔最大

于是我们就得到了这个：

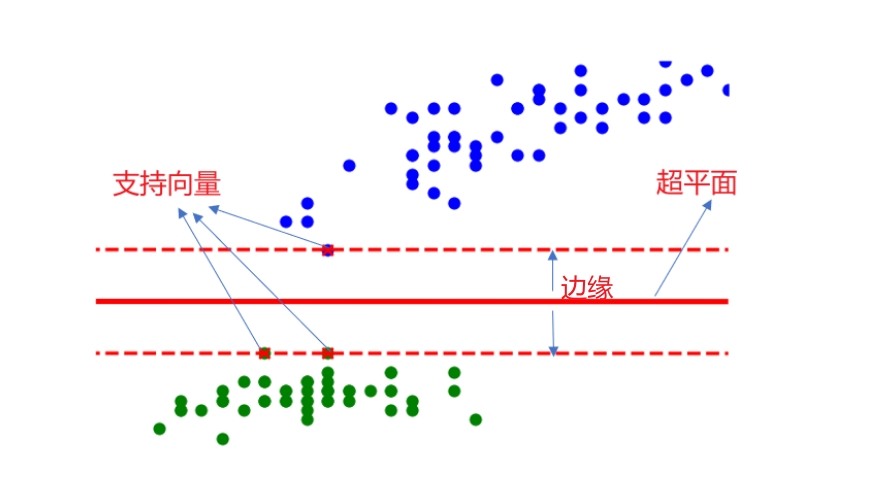
其中超平面方程为：

标签问题：在SVM中我们不用0和1来区分，使用+1和-1来区分，这样会更严格。假设超平面可以将训练的样本正确分类，那么对于任意样本:如果y=+1,则称为正例，y= -1,则称为负例。

现在我们就要确定一个函数可以将任意点进行划分：

整合一下我们可以得到：

点到面的距离公式是：

拓展一下，我们就可以得到点到超平面的距离：

如何找到最优的超平面呢？

超平面可视化：

求解带有约束条件的极值可使用拉格朗日乘子法：

详情可见：【机器学习】拉格朗日乘子法求解最优化问题

现在我们再来考虑线性不可分的情况：

常用的核函数有以下几个：

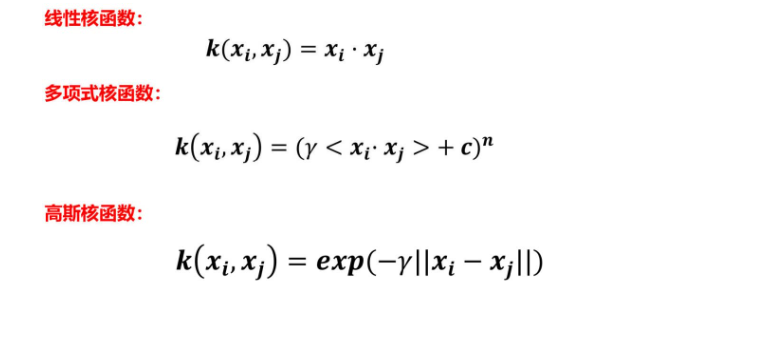
关于高斯核函数中γ值的分析：

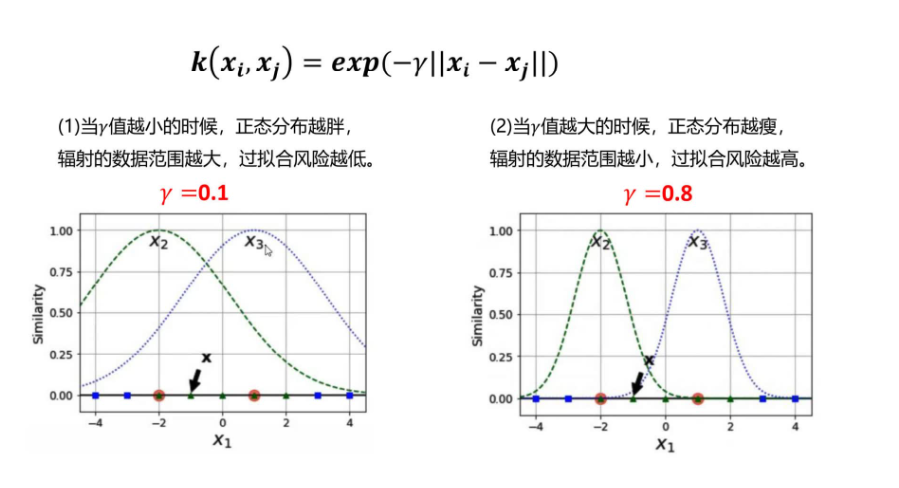
三、svm的优缺点：

优点：

1. 高维数据处理能力： SVM 在高维特征空间中表现出色，适用于处理具有大量特征的数据，如文本分类、图像分类等。

2. 泛化能力强： SVM 在训练集之外的数据上通常有很好的泛化性能，能够有效地处理小样本问题。

3. 支持非线性分类： 通过使用不同的核函数（如多项式核、高斯核等），SVM 可以处理非线性分类问题，将数据映射到更高维度的空间中进行分类。

4. 最大化间隔： SVM 通过最大化超平面与支持向量之间的间隔来选择最佳分类边界，这有助于降低过拟合风险。

5. 鲁棒性： SVM 对于异常值的影响较小，因为它主要依赖于支持向量，而不是整个数据集。

6. 多类别分类： SVM 可以直接用于多类别分类问题，通过一对一（One-vs-One）或一对其余（One-vs-Rest）策略实现。

缺点：

1. 计算复杂性： 在大型数据集上，SVM 的训练时间和内存消耗可能很高，特别是在使用复杂核函数时。

2. 参数调优困难： SVM 有一些超参数需要调整，如正则化参数 C 和核函数的选择，选择合适的参数值需要经验或者使用交叉验证。

3. 不适合非常大规模的数据： 当数据规模非常大时，SVM 的计算和存储要求可能会成为问题。

4. 对非平衡数据敏感： 如果不同类别的样本数量差异很大，SVM 可能会受到不平衡数据分布的影响，需要额外的处理来解决这个问题。

5. 黑盒模型： SVM 通常被认为是黑盒模型，难以解释为什么它做出了特定的预测。

总的来说，SVM 是一个强大的机器学习算法，特别适用于高维、小样本、非线性分类问题。然而，在应用时需要考虑计算复杂性、参数调优和数据规模等因素，并根据具体情况选择是否使用 SVM。