假设检验（超详细）

假设检验

什么是假设检验

假设检验（ hypothesis testing）是指从对总体参数所做的一个假设开始，然后搜集样本数据，计算出样本统计量，进而运用这些数据测定假设的总体参数在多大程度上是可靠的，并做出承认还是拒绝该假设的判断。

为什么要用假设检验

我们在生活中经常会遇到对一个总体数据进行评估的问题，但我们又不能直接统计全部数据，这时就需要从总体中抽出一部分样本，用样本来估计总体情况。这时候就可以用到假设检验，它可以有助于评估出现正确结果的可能性。

假设检验的定义和原理

定义：假设检验是先对总体参数提出一个假设值，然后利用样本信息判断这一假设是否成立。
原理：小概率原理即小概率事件在一次抽样中不发生。
由定义可知，我们需要对结果进行假设，然后拿样本数据去验证这个假设。
所以做假设检验时会设置两个假设：
一种叫原假设，也叫零假设，用H0表示。【希望原假设被接受】
另外一种叫备择假设，用H1表示。【与原假设对立】
接受H0与拒绝H0的方法：看小概率事件是否发生。

假设检验步骤

1先假设H0是真的，然后判别小概率事件是否发生，如果发生，就拒绝H0,接受H1,如果没有发生，就接受H0。解释：整体的思想为小概率事件在一次抽样中不发生，小概率事件不发生是极大概率事件，所以上面的假设就是合理的。
2深入思考，如果小概率事件发生了，此时却拒绝了H0,就是拒绝了真实的情况，那么就犯了第一类错误，即拒真；拒真的概率就是我们所定的α，即显著性水平，一般为0.05。

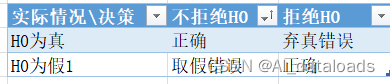
第一类错误：P(拒绝H0|H0真)=α
第二类错误：P(接受HO|H0假)=β

</