邱锡鹏老师团队新发现：首次证明SFT与DPO竟是同一枚硬币的两面，LLM后训练认知被彻底改变

1. 【导读】

论文基本信息

论文基本信息

• 论文标题：Implicit Reward as the Bridge: A Unified View of SFT and DPO Connections

• 作者：Bo Wang、Qinyuan Cheng、Runyu Peng、Rong Bao、Peiji Li、Qipeng Guo、Linyang Li、Zhiyuan Zeng、Yunhua Zhou、Xipeng Qiu

• 作者单位：复旦大学计算机学院、上海人工智能实验室

• 发表信息：arXiv:2507.00018v1 [cs.LG] 15 Jun 2025

• 论文链接：https://arxiv.org/abs/2507.00018

2. 【论文速读】

邱锡鹏老师团队新发表的论文聚焦于预训练语言模型落地真实世界任务的关键后训练阶段，指出从演示或偏好信号中学习在这一适配过程中起着至关重要的作用。文中提出了一个统一的理论框架，旨在架起大型语言模型（LLM）后训练中监督微调（SFT）与偏好学习之间的桥梁。研究表明SFT和直接偏好优化（DPO）等偏好学习方法均在同一最优策略 - 奖励子空间中运行，其中SFT是隐式奖励学习的一种特殊情况。

分析发现传统SFT存在一个关键局限：在优化过程中，分布匹配中的KL散度项相对于策略变为常数，无法对模型更新起到约束作用。为解决这一问题，论文提出了一种简单而有效的降低学习率的方法，该方法带来了显著的性能提升，在指令跟随任务中相对增益高达25%，绝对胜率提高了6%。此外，研究从各种f - 散度函数推导出替代的SFT目标，这些目标在优化过程中保留了KL项，进一步提升了后DPO模型的性能。

3.【研究背景及相关工作】

3.1 研究背景

预训练语言模型需通过后训练阶段适配真实世界任务，当前主要依赖监督微调（SFT） 和偏好学习（如DPO）两种方法，但二者的理论关联长期停留在经验观察层面，缺乏统一理论框架。传统SFT中KL散度项在优化时会退化为常数，无法约束模型更新，而现有研究对SFT与偏好学习框架的理论联系关注不足，制约了对后训练过程的深入理解。

3.2 相关工作

逆强化学习（IRL） 假设专家策略对应最优奖励函数，LLM领域的DPO等方法通过隐式奖励建模降低RLHF计算开销，且已有研究发现DPO中LLM对数几率与Q函数的关联。后训练理论分析虽涉及隐式奖励与学习动态，但未统一阐释SFT与偏好学习的关系。本研究基于f-散度和分布匹配，证明SFT是隐式奖励学习的特例，且二者在同一最优策略-奖励子空间中运行，拓展了对数几率与Q函数的理论关系至SFT场景。

4.【Unified View between SFT and DPO】

4.1 Token-Level MDP in LLM

在语言模型中，马尔可夫决策过程 (MDP)作用于 token 层面的决策。状态表示当前上下文，动作为可能的下一个 token, 策略给出 token 的概率分布。状态转移是确定性的，即 (将 token 附加到上下文)。模型每选择一个 token 会获得奖励,直至到达终止状态，其中为折扣因子。该框架形式化了语言模型在文本生成过程中的序列决策机制 ,

4.2 后训练中的分布匹配

模仿学习的核心训练目标是分布匹配，即最小化专家状态- 动作分布与策略模型分布之间的 f- 散度。针对 LLM, 传统的熵正则项被修改为基础模型与策略模型之间的 KL 散度，以保留预训练阶段形成的自然语言先验：。其中为 f- 散度，为超参数。这一调整避免了对整个词表进行概率平均，防止破坏预训练模型的知识。

4.3 作为隐式奖励发现的模仿学习

通过非对抗模仿学习的推导，最小化 f- 散度等价于先学习任意奖励函数下的最优策略，再优化该奖励函数， 其等价目标为：其中是 f- 散度的凸共轭函数。具有闭式解，将策略优化与奖励发现关联起来。当选择总变异散度时，传统 SFT 目标可视为该框架的特例，其损失函数退化为最大似然估计 (MLE)形式。

4.4 SFT与DPO统一性的关键结论

1. SFT作为隐式奖励学习的特例：SFT和DPO均在同一最优策略-奖励子空间中运行。SFT沿专家演示的平均梯度方向搜索，而DPO沿“选择-拒绝”样本的方向向量优化，二者均旨在建模数据中隐含的奖励函数 。

2. 传统SFT的局限性：SFT中的KL散度项在优化时退化为常数，无法约束模型更新。通过降低学习率可缓解该问题，在指令跟随任务中实现最高25%的相对增益和6%的绝对胜率提升 。

3. 替代SFT目标函数：使用 Pearson χ²、平方 Hellinger 等 f - 散度可保留 KL 项，避免数值不稳定，进一步提升 DPO 后模型的性能，绝对胜率最高增加 4%。

4.5 SFT中LLM对数几率作为Q函数

在 SFT 过程中，LLM 的对数几率对应于学习到的隐式奖励的 Q 函数：

其中 仅依赖状态， 为隐式奖励函数。这一结论将 DPO 中对数几率与 Q 函数的关系扩展到 SFT 场景，支持通过对数几率的 loq-sum-exp 估计状态值函数。实验表明，LIM 对数几率在不同模型间对状态质量的排序具有一致性，验证了其作为值函数的性质

5.【实验结果分析】

5.1 小学习率SFT对Post-DPO模型的提升

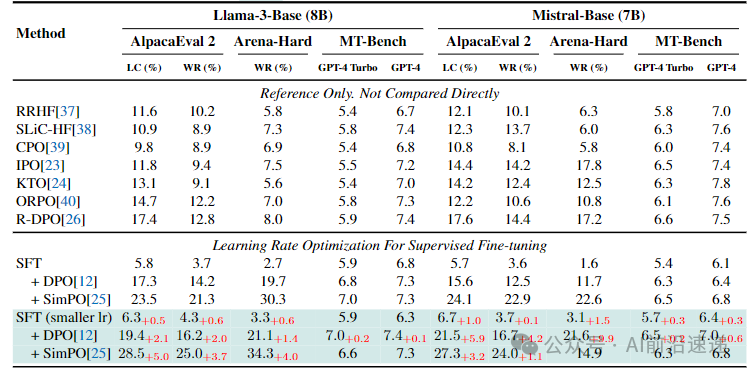
• 实验设置：在SFT阶段将学习率从常用的降低至（Llama3-8B）和（Mistral-7B），后续DPO和SimPO算法的超参数保持不变，使用UltraChat-200K进行SFT、Ultra-feedback进行DPO，评估基准包括AlpacaEval2、Arena Hard、MT-bench 。

• 关键发现：

  • Llama3-8B：SFT小学习率使DPO后的AlpacaEval2胜率从17.3%提升至19.4%（+2.1%），SimPO结果从23.5%提升至28.5%（+5.0%），GPT-4 Turbo在Arena Hard的胜率提升4.0% 。

  • Mistral-7B：DPO后AlpacaEval2胜率从15.6%提升至21.5%（+5.9%），GPT-4在MT-bench的胜率提升0.6%，相对增益达25% 。

• 结论：降低SFT学习率可减少KL项缺失导致的模型更新偏差，使Post-DPO模型更接近基模型分布，验证了学习率调整对缓解传统SFT局限性的有效性 。

  

5.2 替代f-散度目标对Post-DPO的优化

• 实验设置：采用Pearson  和 Squared Hellinger 散度推导SFT目标函数，对比传统总变异散度的效果，避免对数/指数计算的数值不稳定问题 。

• 关键结果：

  • Pearson-SFT + DPO：Llama3-8B在Arena Hard的GPT-4 Turbo胜率从21.1%提升至24.7%（+3.6%），Mistral-7B的AlpacaEval2胜率从21.5%提升至23.1%（+1.6%） 。

  • SH-SFT + DPO：Mistral-7B在Arena Hard的GPT-4 Turbo胜率提升4.2%，且SFT阶段损失曲线更稳定 。

• 结论：保留KL项的f-散度目标可约束模型更新步长，尽管单独SFT性能可能弱于传统方法，但Post-DPO的性能提升验证了KL正则化的重要性。

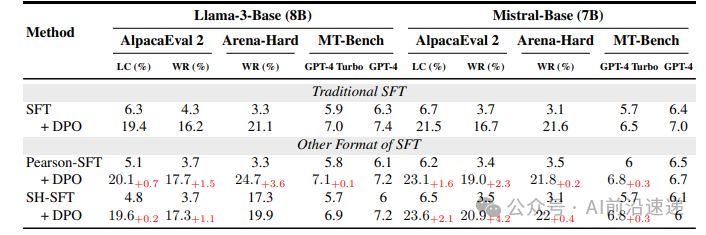
Downstream results for different training targets and their corresponding post-DPO checkpoints

5.3 LLM对数几率的值函数特性验证

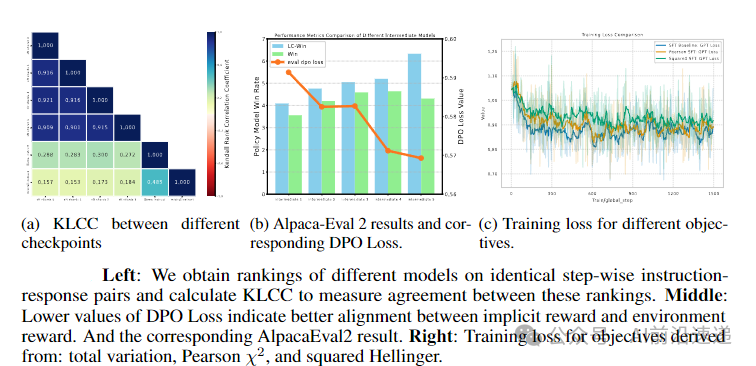
• 实验设计：将UltraChat-200K分为4份进行SFT，结合Llama3-instruct和Zephyr模型，在MATH-500验证集上提取logits计算log-sum-exp，通过Kendall秩相关系数（KLCC）评估状态质量排序的一致性 。

• 量化结果：

  • 同一数据集拆分的4个模型间KLCC接近1，不同数据集训练的模型（如Zephyr与Llama3-instruct）的KLCC仍为正，表明logits对状态质量的评估具有跨模型一致性 。

  • 隐式奖励与下游奖励的对齐度（如AlpacaEval2的DPO损失）与模型胜率正相关，DPO损失降低对应胜率提升约0.184% 。

• 理论意义：证实SFT过程中logits可作为隐式奖励的Q函数，支持无需蒙特卡洛采样的状态值估计，为理解SFT的对齐机制提供了实证依据 。

5.4 隐式奖励的稳定性分析

• 实验方法：绘制SFT训练过程中初始响应token的log-sum-exp曲线（即），并对早期SFT checkpoint进行DPO评估 。

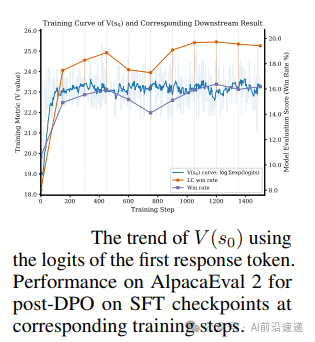
• 核心观察：

  • 在150步内快速收敛，表明SFT能有效将随机初始奖励校准至合理范围，后续训练主要进行细调 。

  • 早期checkpoint（如SFT 150步）的Post-DPO胜率与完整SFT的结果趋势一致，验证了SFT对隐式奖励的稳定作用 。

• 实际价值：为SFT的早期终止策略提供参考，暗示无需完整训练即可实现隐式奖励的基础对齐，减少计算开销 。

7.【论文总结展望】

总结

论文提出统一理论框架，证明监督微调（SFT）与直接偏好优化（DPO）均在最优策略-奖励子空间中运行，SFT是隐式奖励学习的特例。传统SFT中KL散度项在优化时退化为常数，导致模型更新缺乏约束，通过降低SFT学习率（如Llama3-8B降至5×10⁻⁶）可提升Post-DPO模型性能，相对增益达25%。此外，基于Pearson χ²、Squared Hellinger等f-散度推导的替代SFT目标能保留KL项，进一步提升模型表现，且LLM对数几率在SFT中可作为隐式奖励的Q函数，为后训练提供理论支撑。

展望

未来可探索SFT与DPO的多目标联合优化，解决当前顺序训练中目标冲突问题（如交错训练导致性能波动）。同时，需实验验证更多f-散度（如KL、JS散度）在LLM后训练中的有效性，设计专门算子解决数值不稳定问题。此外，模型隐式奖励学习机制或推动LLM环境意识与意识属性的哲学探讨，拓展人工智能伦理研究边界。