JLU吉林大学人工智能原理期末重点算法以及习题

吉林大学研究生人工智能原理复习总结，希望可以给学弟学妹一些参考~

产生式系统基本过程：PRODUCTION算法

控制策略的应用：

（1）4步中如何选取规则R

可分解产生式系统的基本过程：SPLIT算法

控制策略的应用：

（1）5步中如何选取D*

（2）7步中如何选规则R

回溯过程BACKTRACK

一般的图搜索过程GRAPHSEARCH

AO*算法求最佳解图，最终的G’即是最佳解图。同时还有找出几个不同的解图，并计算其费用

普通解图费用计算方法：

α-β剪枝：

求子句集方法（用到Skolem范式化）

构造公式G对应解释I的H解释（教材P76）
先求H域、再求原子集、再求H解释

S中有常量情况：

S中没有常量情况：

替换乘积

合一算法

Herbrand两条定理:

a.DP过程：（利用Herbrand定理）

b.归结原理：（改进Herbrand定理，归结原理的本质思想是检查子句集S是否包含一个空子句□）

若从子句集S可演绎出空子句，则S是不可满足的

c.扩展规则（和归结原理类似，也可以证明子句集的不可满足性）

d.表推演（也可证明公式恒真、恒假、可满足性等；有命题的表推演以及一阶逻辑的表推演）

命题逻辑的表推演：

基于规则的正向演绎系统题型

1.事实、规则、目标化为标准型；

2.画与或图；

3.替换集合相容性，合一复合替换；

4.解图对应的全部子句：

事实：

1. 逻辑公式化为不含蕴涵符的AND/OR形式，再用与或图表示（注意这部分与或图画法与前面相反，或有弧）
2. 过程类似Skolem范式化，但是不要求母式是合取形式，要求不同主合取项的变量使用不同名字

规则：

F规则的形式：L→W，是正常Skolem化后恢复成蕴涵式，且要求：

    L是单文字；

    W是AND/OR形公式；

    出现在蕴涵式中的所有变量假定是对整个蕴涵式全称定量的；

    不同规则使用的变量名互不相同；

    规则与事实AND/OR图中的变量名也不相同。

    Note:正向演绎系统的规则的前提必须是单文字，看起来似乎限制很强。但是，很多逻辑公式可以转换成满足这种限制的规则.

    例如，形式为（L1∨L2）→W的蕴涵式等价于两条规则

                L1→W和L2→W。

例子：

目标：

目标公式形式：文字的析取形式。

   （1）当目标公式包含存在定量和全称定量的变量时，是经对偶Skolem化后的文字的析取形式；

   （2）对公式中的变量进行改名，使得不同的析取项中没有相同的变量。

Note:对偶Skolem化：全称量词用存在量词的Skolem函数所代替，然后把存在量词删去，出现的变量假定都是存在定量的。

     改名依据:$x(W1(x) ∨W2(x))=$xW1(x)∨ $yW2(y)

在与或图上画法：

八数码问题，画出使用A算法的启发式搜索过程图？

计算渗透度 渗透度能否完全衡量搜索算法启发能力？

证明：OPEN表中满足f(n)<f*(s)的节点n最终一定被算法选出来扩展（18年）

用回溯BACKTRACK求解四皇后问题

设计一个BACKTRACK改进算法，并求解四皇后，改进如下：

产生式系统表示问题

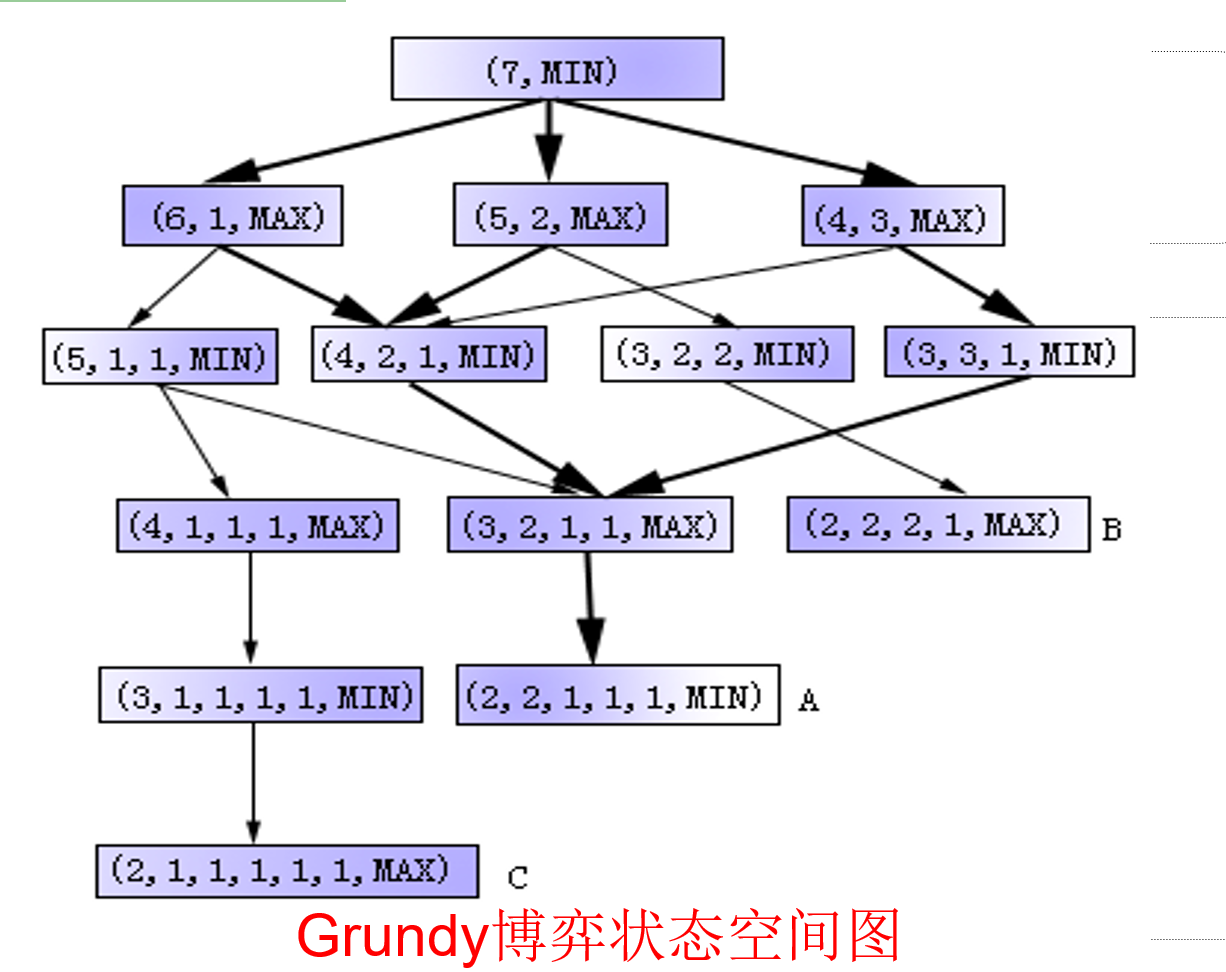
分钱币，画出博弈图证明后走的一方一定能赢

语义树相关题型四问：

1. 求H域 原子集
2. 写出某个子句的所有基例
3. 画出子句集S的完全语义树与封闭语义树，指出所有失效点和推理点
4. 写出被封闭语义树中失效点弄假的S的所有基例集合

归结原理改进方法进行归结：

支架集归结

语义归结

输入归结

锁归结策略

Herbrand解释与普通解释对应关系