7.9.红黑树的插入

一.红黑树的插入操作：

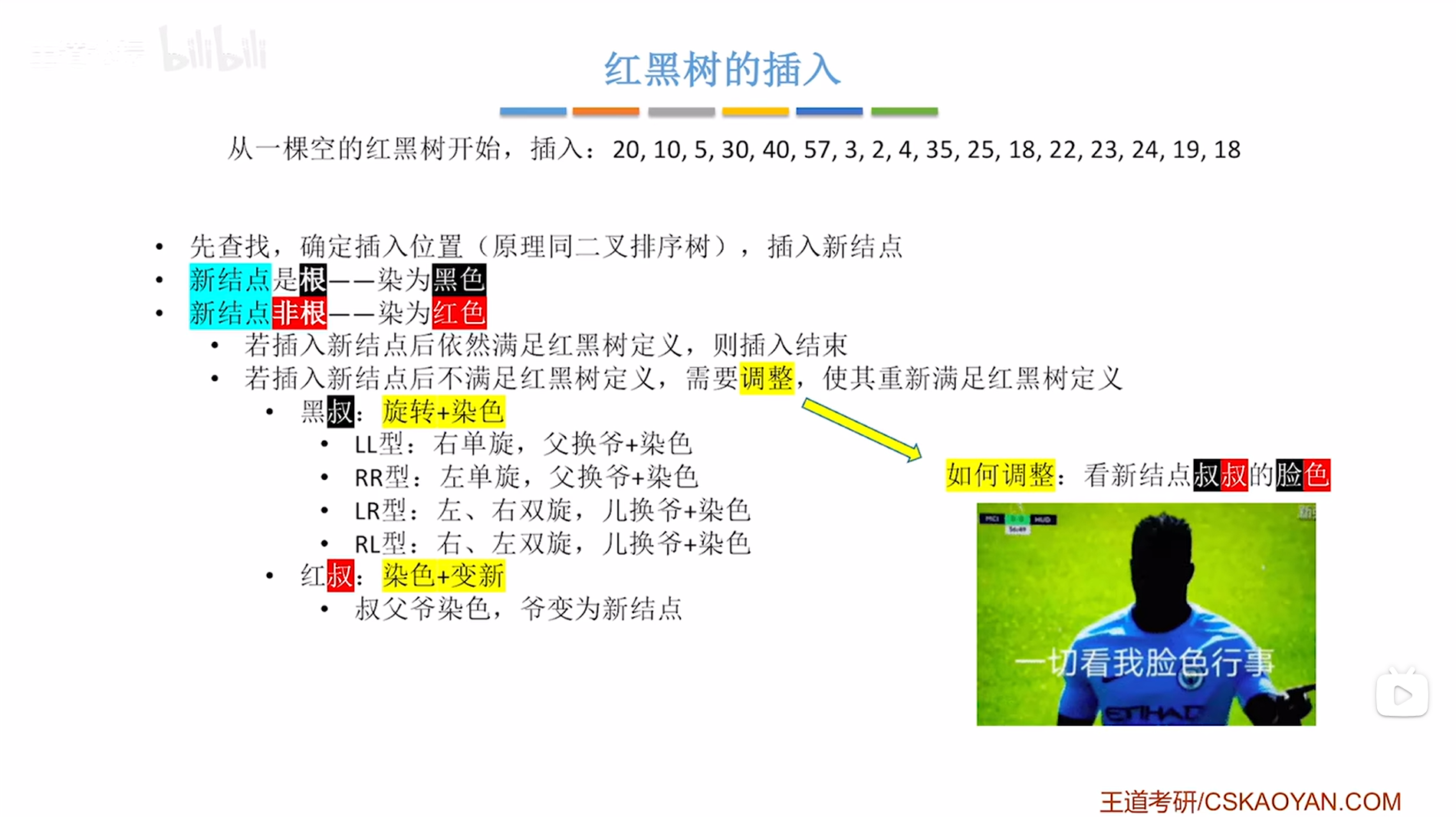
1.红黑树插入操作的实现步骤：

• 判断属于LL型、RR型、LR型、RL型需要通过新插入的结点相对于它的爷爷结点的位置来判断，比如新插入的结点在爷爷结点的左孩子的左子树上，就是LL型（爷爷结点就是某个结点的父结点的父结点）

• 有关叔叔结点的判断详情见"5.1.树的定义和基本术语"

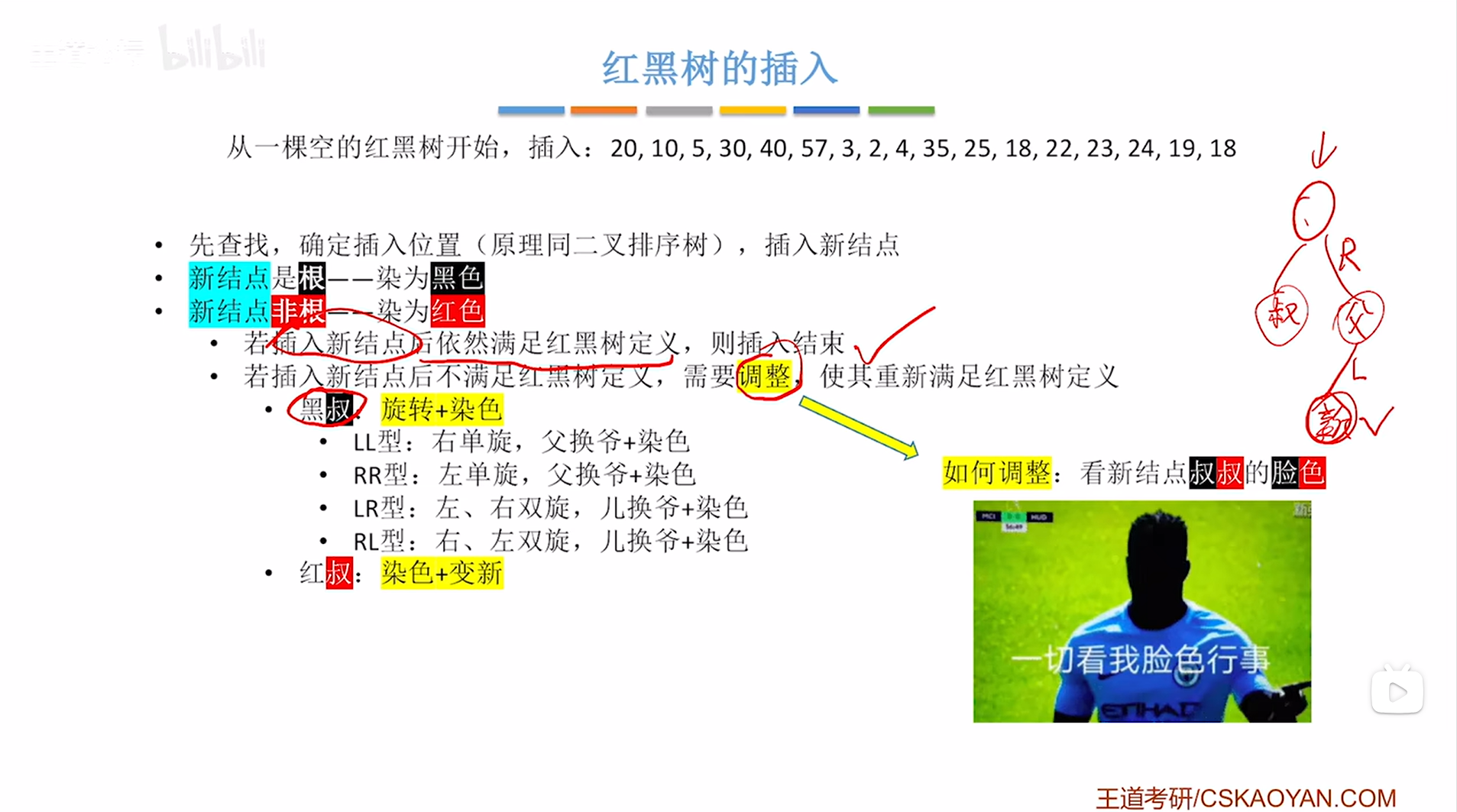
• 某个结点的叔叔结点就是该结点的父结点的兄弟结点；某个结点的爷爷结点就是该结点的父结点的父结点，如下图：

2.实例：

注：红黑树未必是平衡二叉树，但红黑树一定是二叉排序树。

以上述图片为例，

从一棵空的红黑树开始，

首先要插入结点20，空树中第一个插入的结点一定是根结点，根据红黑树的性质可知根结点必须是黑色的，

所以结点20要涂黑，

如下图：

如上图，

此时满足红黑树的定义，

蓝色的框表示新插入的结点，NULL LEAF是叶子结点，

接下来要插入结点10，根据二叉排序树的插入规则从根结点20出发，由于10小于20，所以要到20结点的左子树，

此时20结点的左子树为叶子结点即NULL LEAF，所以10要插在该位置，

只要新插入的结点不是根结点，那么就一律涂红，

如下图：

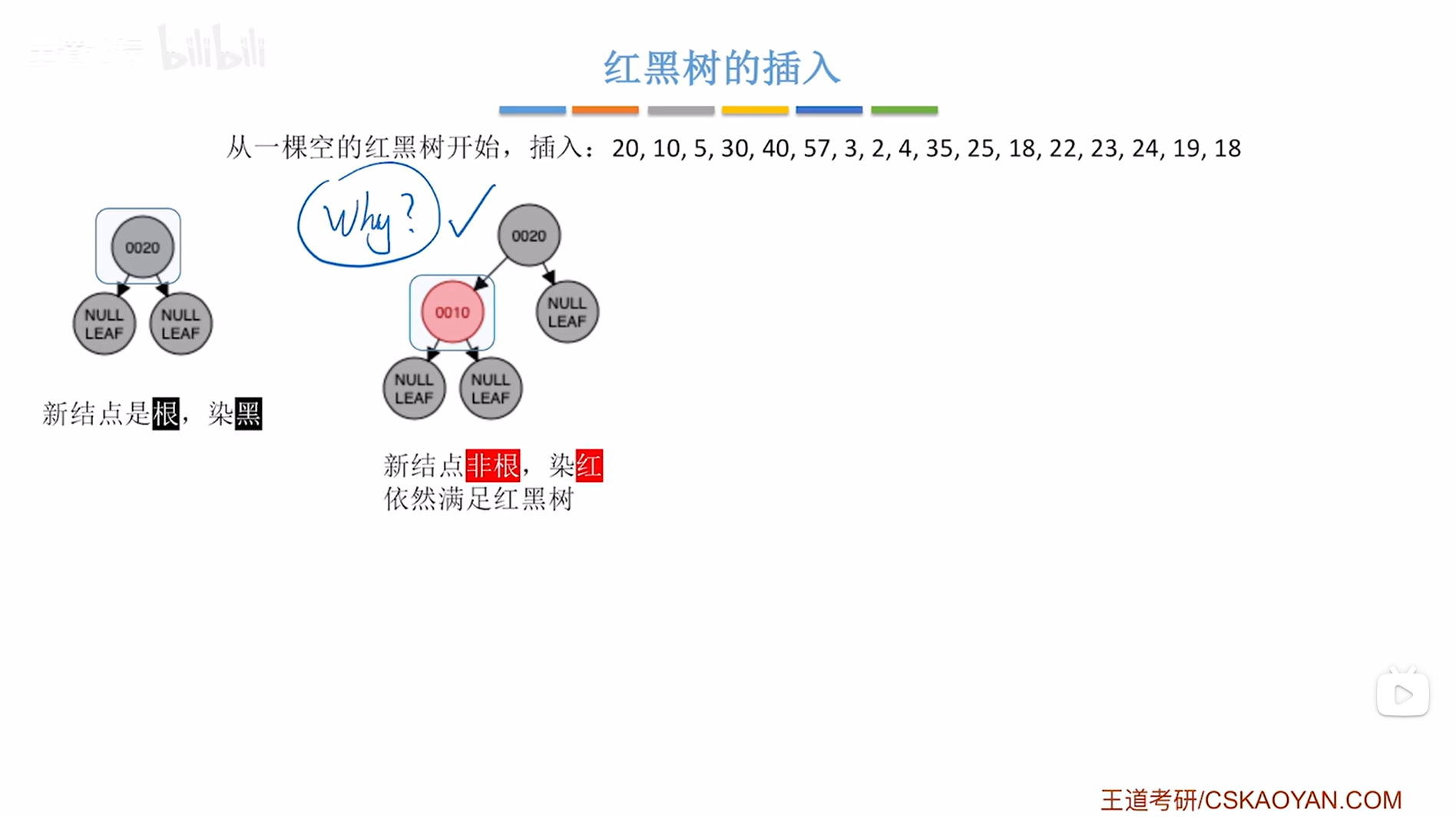
如上图，

此时满足红黑树的定义。

思考？为什么插入非根结点要涂成红色，这么做是为了保证"黑路同"的特性。

比如刚才新插入的结点10涂成黑色，就会导致根结点20到达左边的叶子结点即20->10->NULL LEAF要比到达右边的叶子结点即20->NULL LEAF经过的黑色结点数量要多，就不符合红黑树"黑路同"的特性，

因此新插入的新结点如果是非根结点，且涂成黑色，那么一定会破坏"黑路同"的特性，

所以每插入一个新结点，会优先把该结点涂成红色，因为红结点不会增加黑路的长度，

由于插入结点10后没有破坏红黑树的特性，因此不需要调整。

接下来要插入结点5，根据二叉排序树的插入规则可知结点5要插在结点10的左子树上，并把结点5涂红，

如下图：

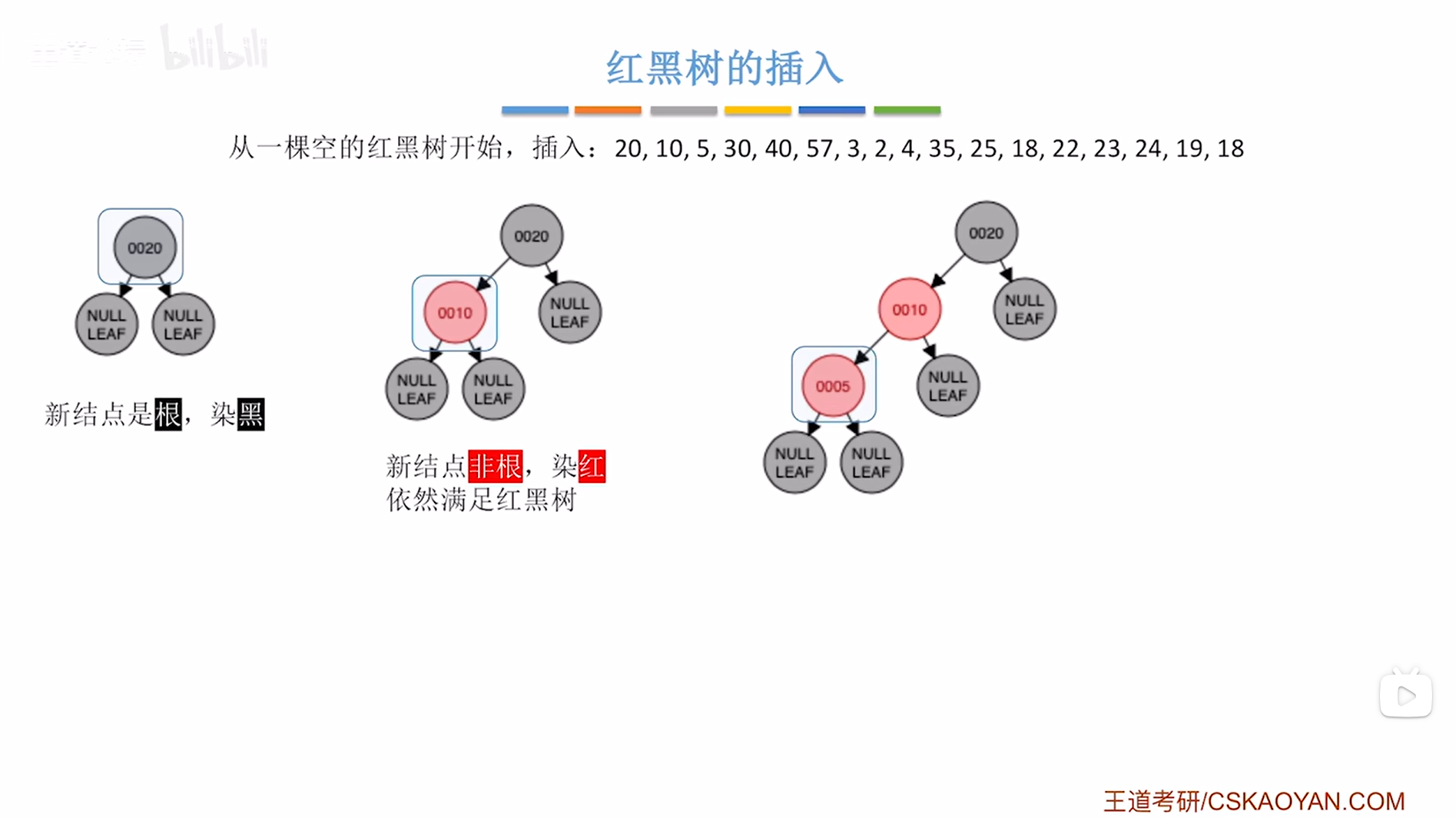
如上图，

此时结点5违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点5的叔叔结点的颜色，

结点5的父结点是10结点，10结点的兄弟结点是NULL LEAF结点(20结点的右孩子)，

所以结点5的叔叔结点是NULL LEAF结点(20结点的右孩子)，NULL LEAF结点(20结点的右孩子)是黑色结点，

因此需要"旋转+染色"->

由于10结点的父结点是20结点，所以结点5的爷爷结点是20结点，

因此结点5属于LL型即"新插入的结点5位于它的爷爷结点20的左孩子的左子树上"，

对于LL型的处理方法首先要右单旋使得父换爷，再进行染色->每一次的旋转操作都会使得儿子变为爹，原来的爹变为儿子；染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

其中结点5的父结点是10，爷结点是20，

通过右单旋让父结点10替代爷结点20的位置，

20结点会变为结点10的儿子，且原本的爷结点20要放在10结点的右孩子上，因为要保证二叉排序树的特性"左<根<右"，

旋转之后还需要染色，对于染色，处理的仍旧是父结点10和爷结点20，

父结点10原本是红色，染色后为黑色，爷结点20原本是黑色，染色后为红色，

如下图：

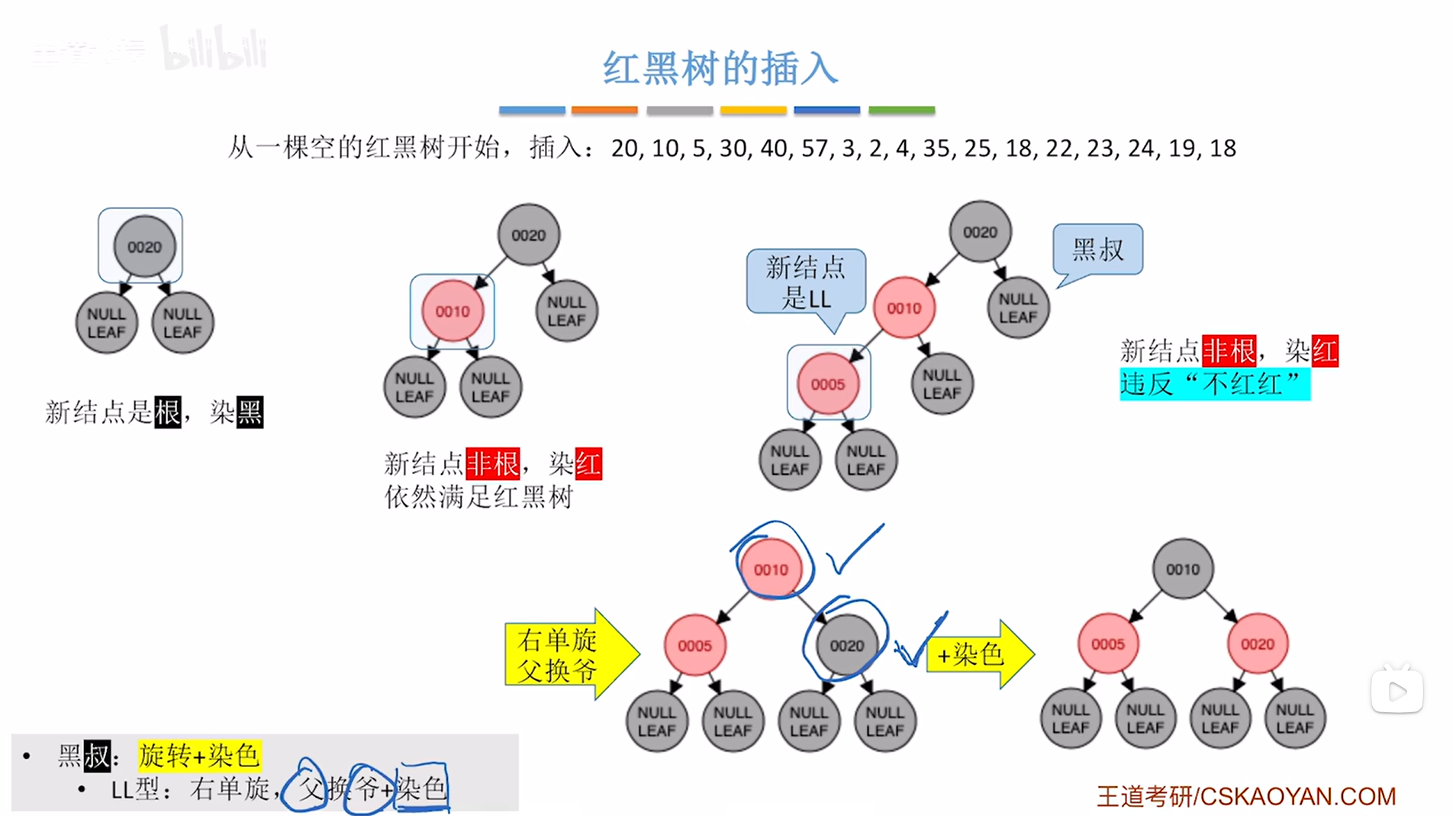
如上图，

此时满足红黑树的定义。

接下来要插入结点30，根据二叉排序树的插入规则可知结点30要插在结点20的右子树上，并把结点30涂红，

如下图：

如上图，

此时结点30违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点30的叔叔结点的颜色，

结点30的父结点是20结点，20结点的兄弟结点是5结点，

所以结点30的叔叔结点是5结点，5结点是红色结点，

因此需要"染色+变新"即叔父爷染色，爷变为新结点->

首先"叔父爷染色"，其中新插入的结点30的叔结点是5结点、父结点是20结点、爷结点是10结点，

进行叔父爷染色，染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

如下图：

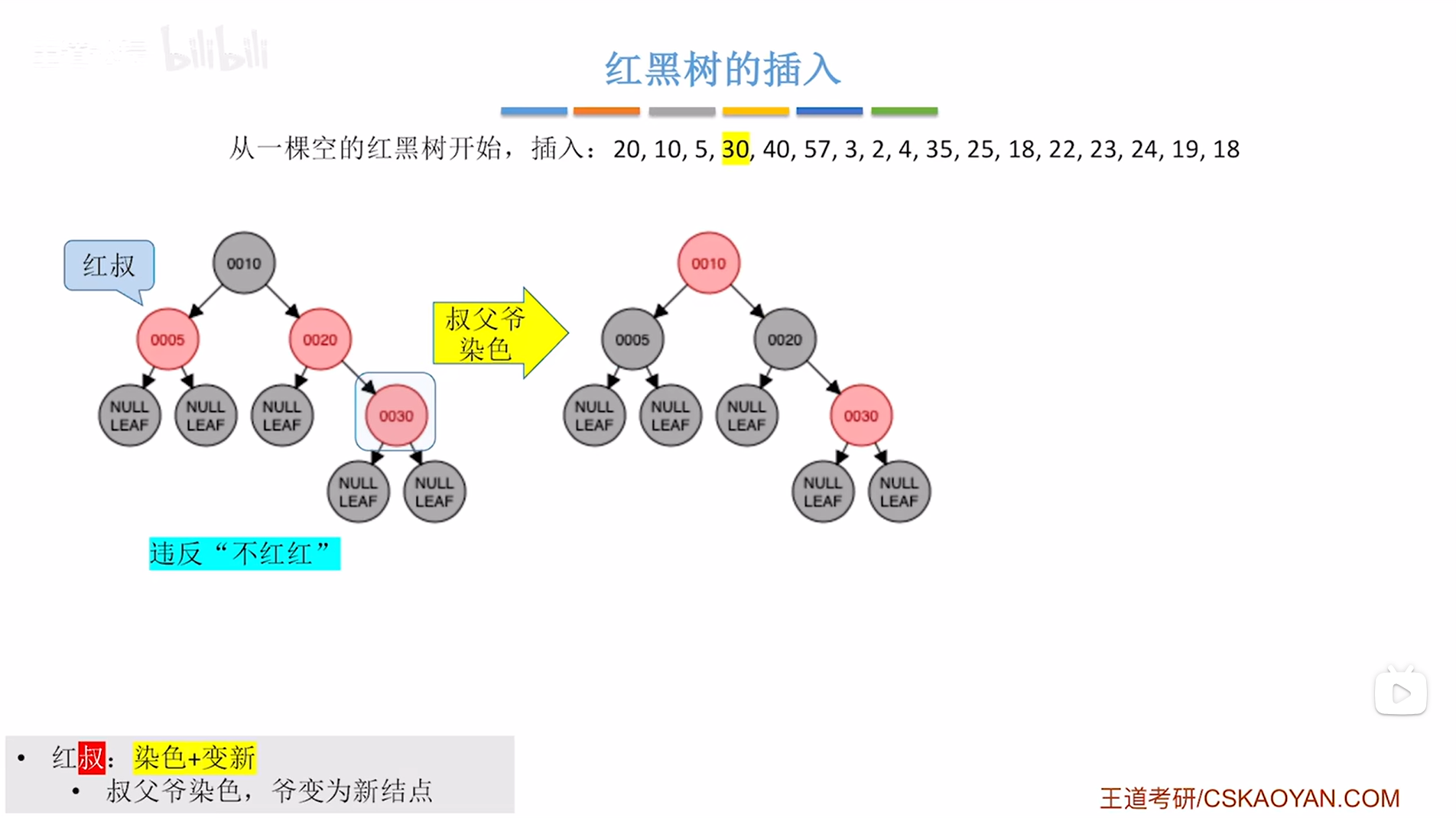
如上图，

再进行"爷变为新结点"，这一步针对于新插入的结点30的爷结点10，

这里要把爷结点10看作新插入的结点，再做调整，

根据"如果新结点是根结点，那么染为黑色；新结点非根，那么染为红色"可知，

由于爷结点10位于根结点的位置，所以把爷结点10染黑，

如下图：

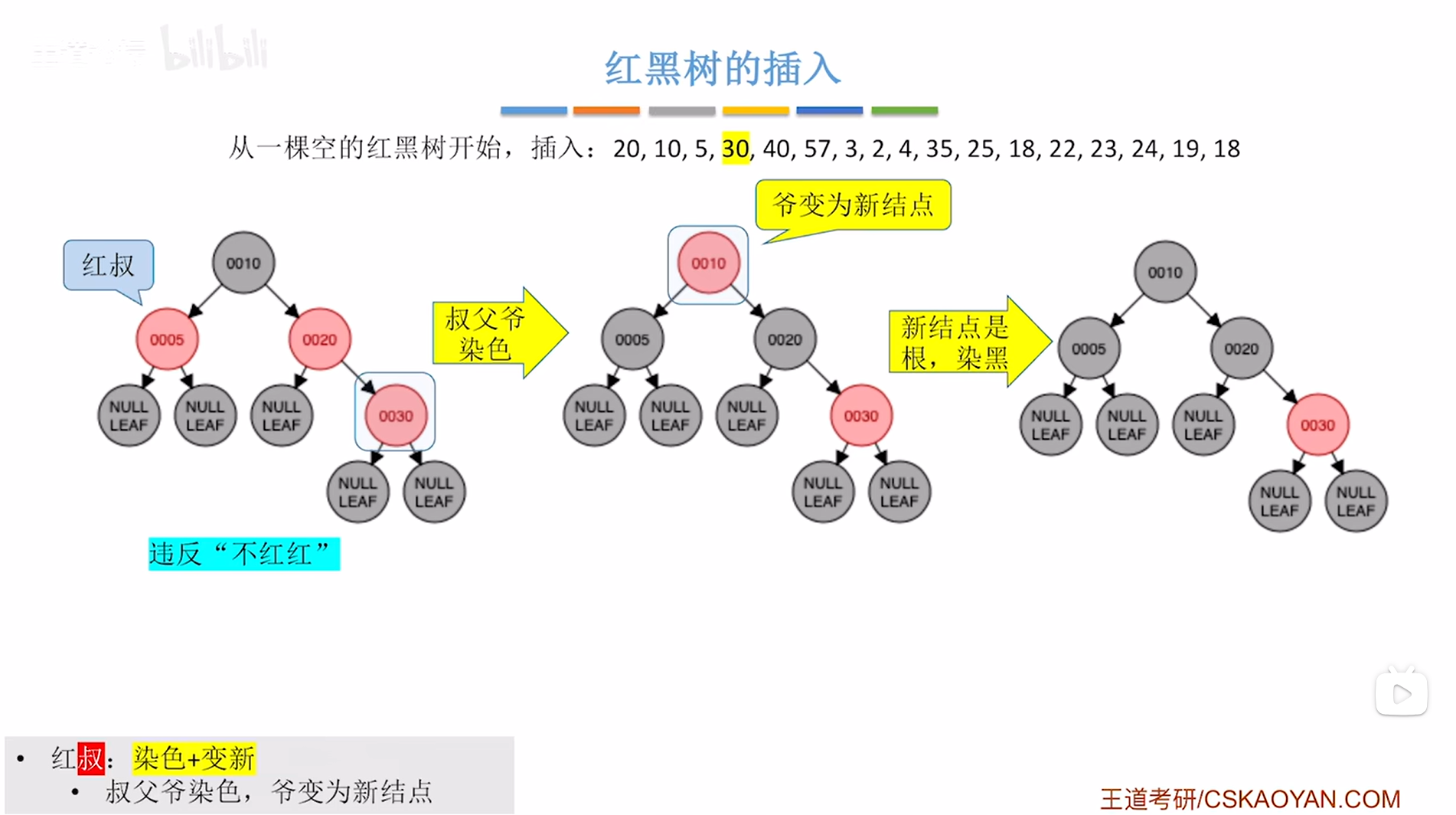
如上图，

此时满足红黑树的定义。

接下来要插入结点40，根据二叉排序树的插入规则可知结点40要插在结点30的右子树上，并把结点40涂红，

如下图：

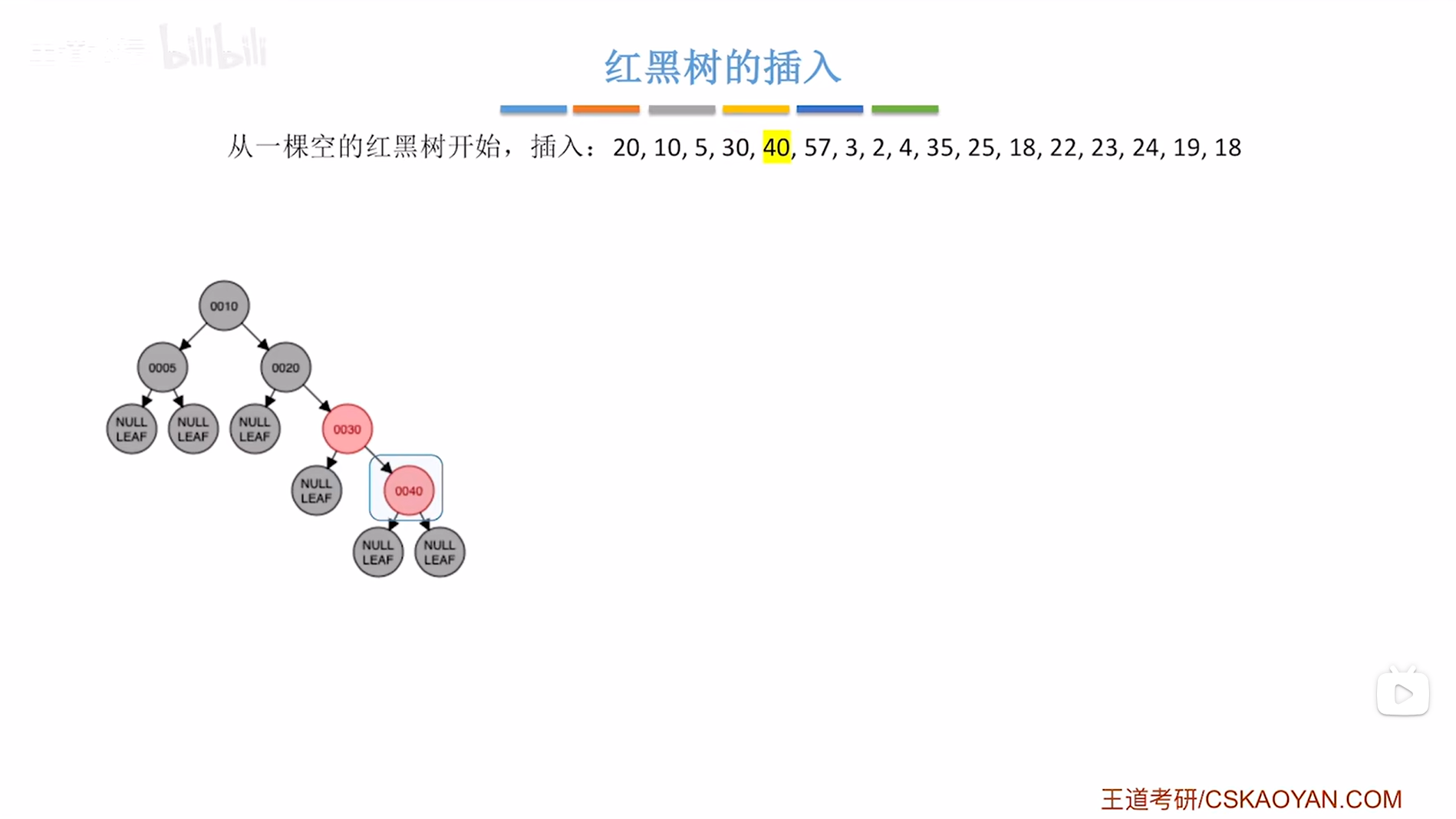
如上图，

这时会发现每插入一个新结点之后，这个新结点一定会破坏原来红黑树"不红红"的特性，为什么？

第一个特性"左根右"一定不会被破坏，因为在插入新结点之前要根据"左根右"判断放到左子树还是右子树；

第二个特性"根叶黑"一定不会被破坏，因为根结点一定是黑色的，而叶子结点是虚拟的，本质是一个空指针，叶子结点也被视为黑色；

第三个特性"黑路同"一定不会被破坏，因为插入非根结点时都染为红色，红结点的加入不会导致它上方的任何一个结点的黑路变长，它下方的任何一个结点的黑路更不会受到影响，

所以每次新插入一个结点之后，如果插入的结点不是根结点，要判断这个结点有没有破坏红黑树的特性，只需要重点判断是否违反"不红红"的特性，

显然40结点的插入违背了红黑树"不红红"的特性，

如下图：

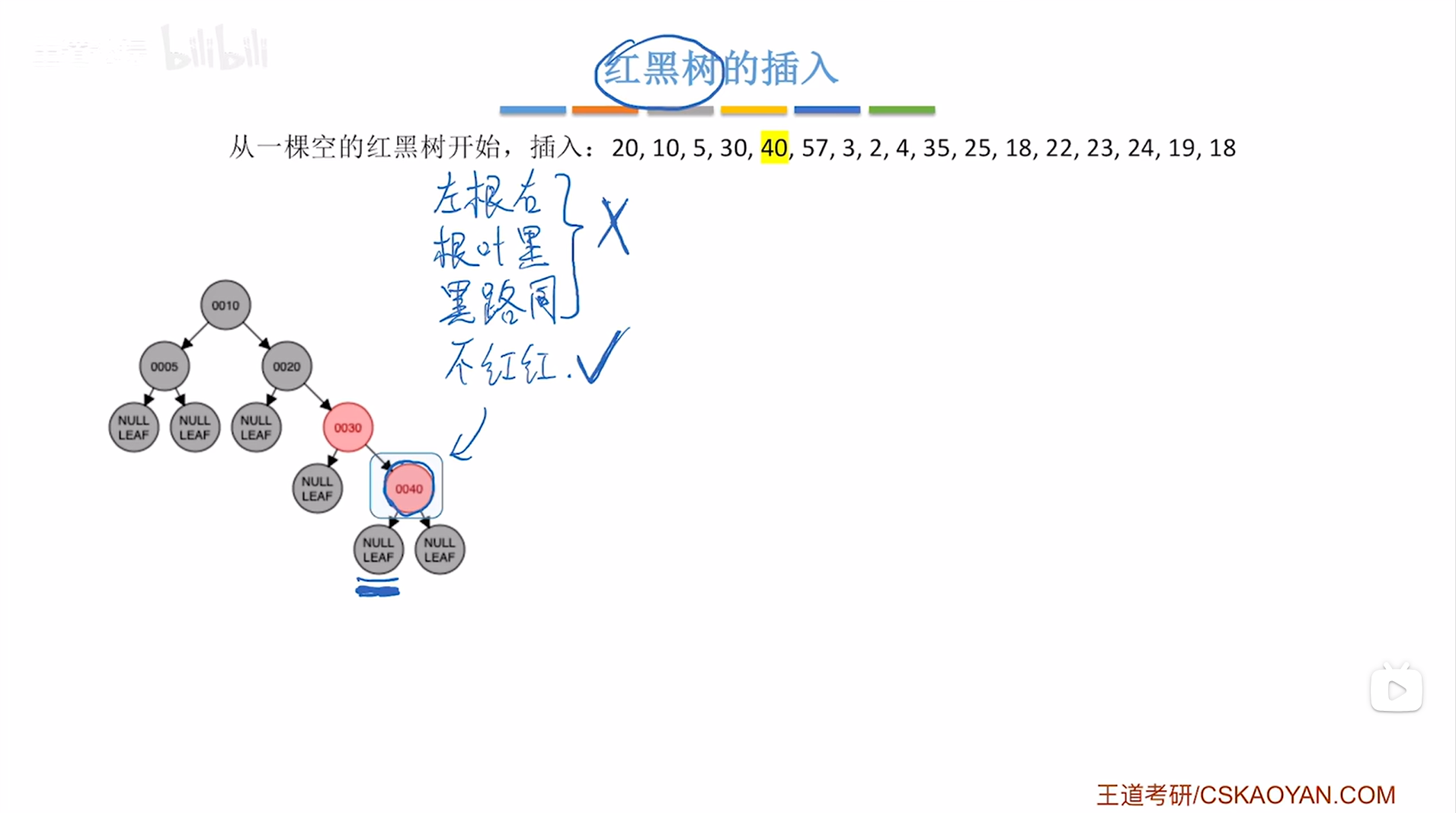
如上图，

此时结点40违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点40的叔叔结点的颜色，

结点40的父结点是30结点，30结点的兄弟结点是NULL LEAF结点(20结点的左孩子)，

所以结点40的叔叔结点是NULL LEAF结点(20结点的左孩子)，NULL LEAF结点(20结点的左孩子)是黑色结点，

因此需要"旋转+染色"->

由于30结点的父结点是20结点，所以结点40的爷爷结点是20结点，

因此结点40属于RR型即"新插入的结点40位于它的爷爷结点20的右孩子的右子树上"，

对于RR型的处理方法首先要左单旋使得父换爷，再进行染色->就是把父结点换到爷结点的位置，爷结点成为父结点的儿子，每一次的旋转操作都会使得儿子变为爹，原来的爹变为儿子；染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

其中结点40的父结点是30，爷结点是20，

通过左单旋让父结点30替代爷结点20的位置，

结点20会变为结点30的儿子，且原本的爷结点20要放在30结点的左孩子上，因为要保证二叉排序树的特性"左<根<右"，

旋转之后还需要染色，对于染色，处理的仍旧是父结点30和爷结点20，

父结点30原本是红色，染色后为黑色，爷结点20原本是黑色，染色后为红色，

如下图：

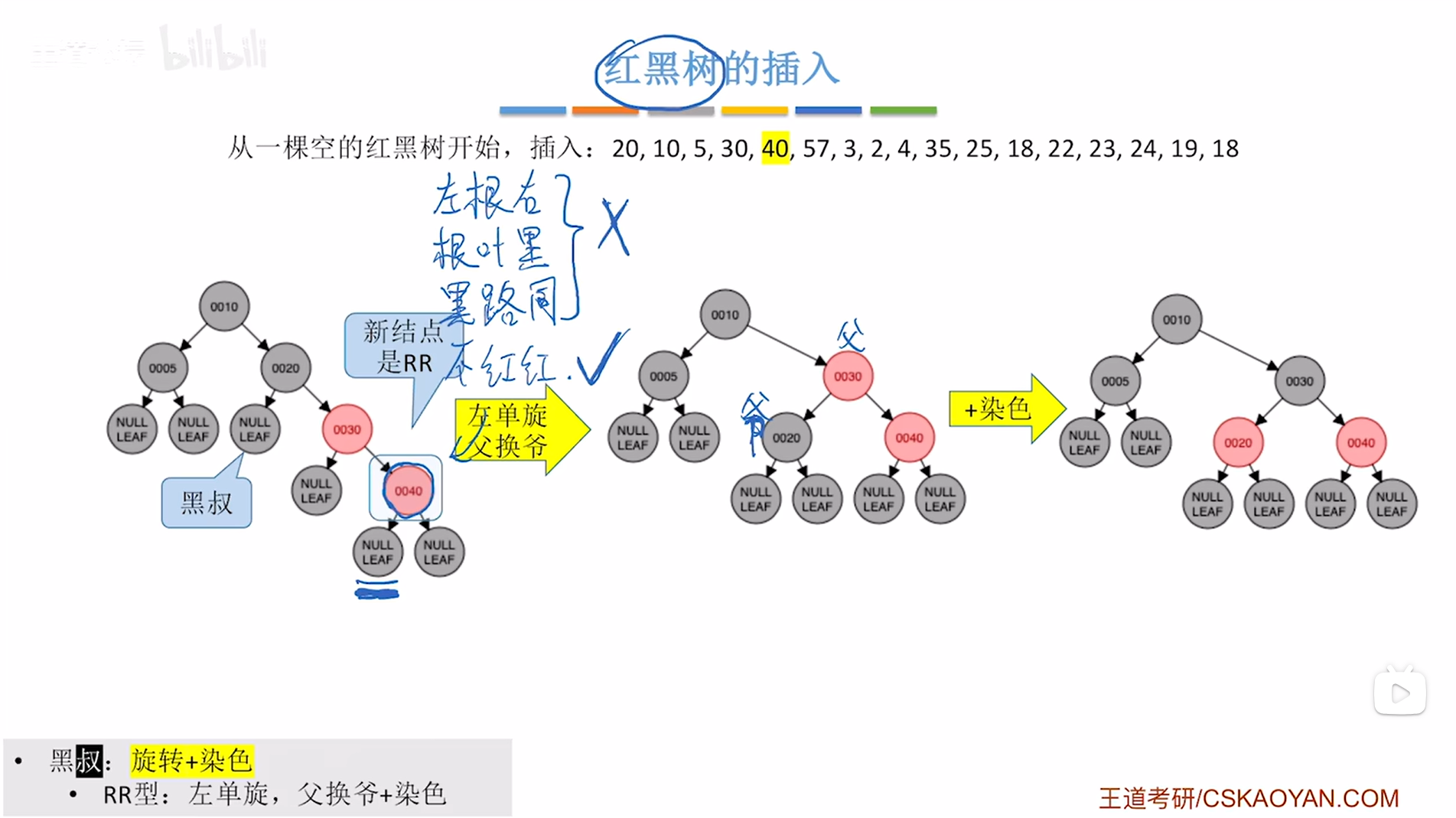
如上图，

此时满足红黑树的定义。

接下来要插入结点57，根据二叉排序树的插入规则可知结点57要插在结点40的右子树上，并把结点57涂红，

如下图：

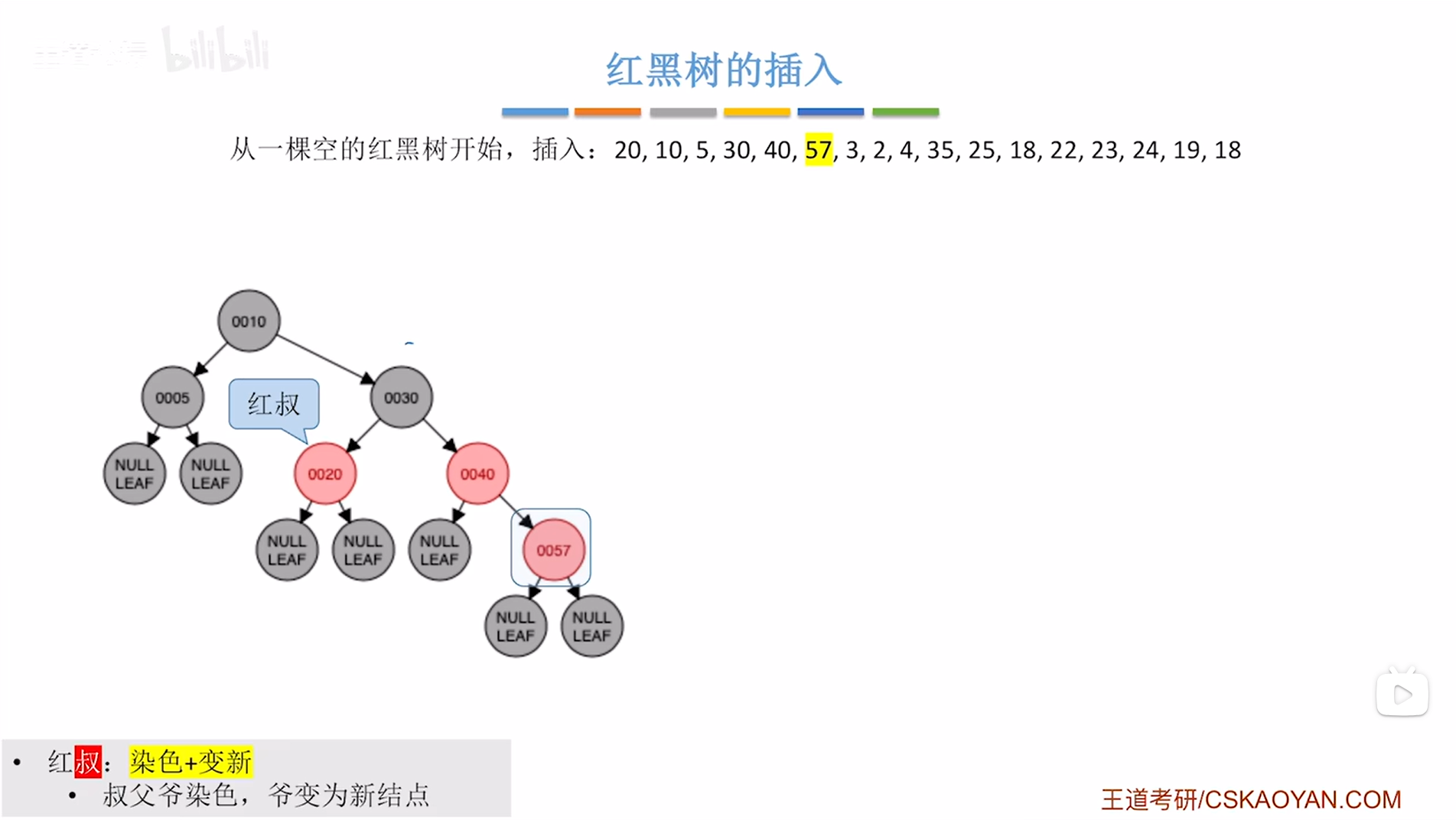
如上图，

此时结点57违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点57的叔叔结点的颜色，

结点57的父结点是40结点，40结点的兄弟结点是20结点，

所以结点57的叔叔结点是20结点，20结点是红色结点，

因此需要"染色+变新"即叔父爷染色，爷变为新结点->

首先"叔父爷染色"，其中新插入的结点57的叔结点是20结点、父结点是40结点、爷结点是30结点，

进行叔父爷染色，染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

如下图：

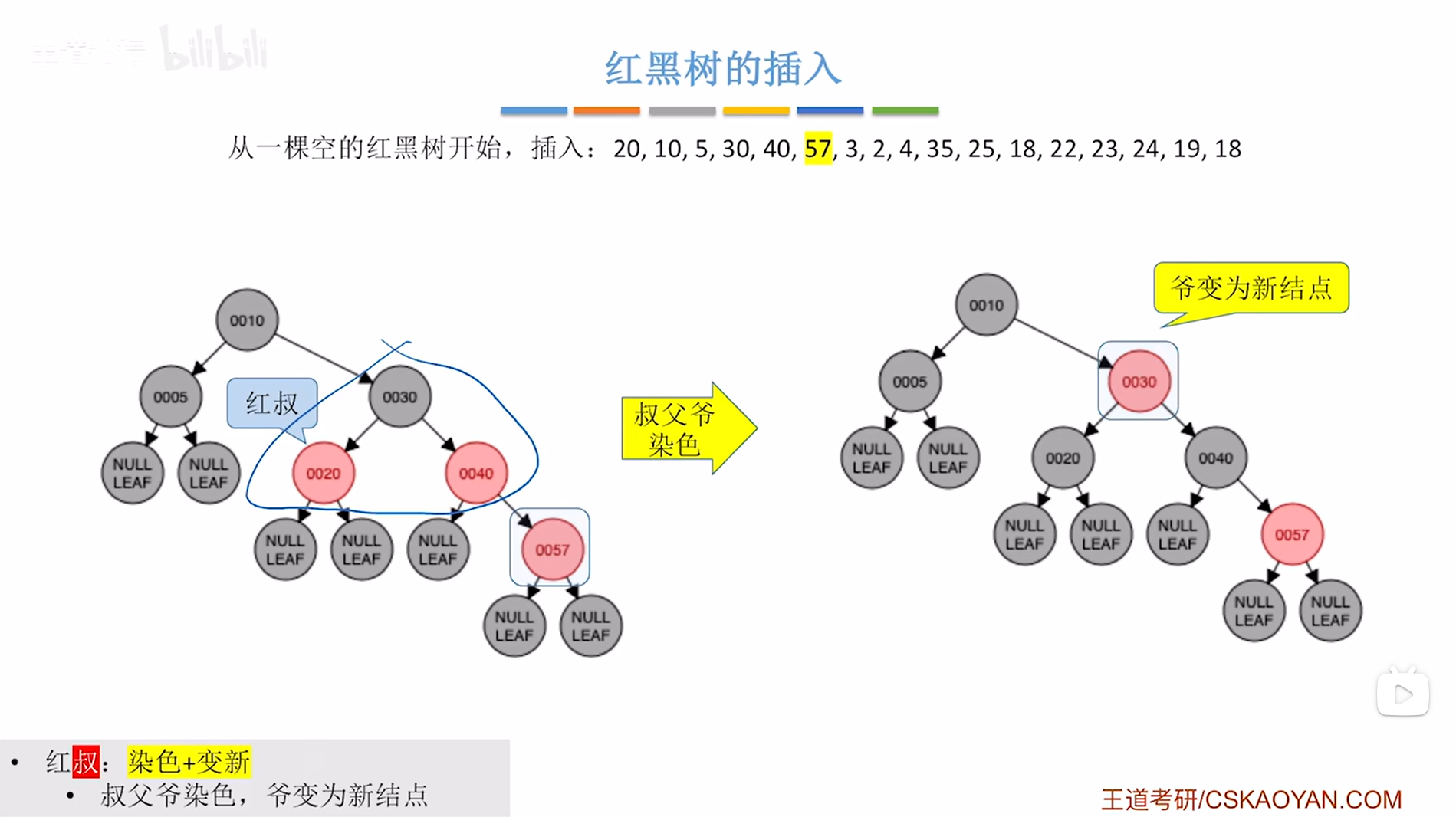
如上图，

再进行"爷变为新结点"，这一步针对于新插入的结点57的爷结点30，

这里要把爷结点30看作新插入的结点，再做调整，

根据"如果新结点是根结点，那么染为黑色；新结点非根，那么染为红色"可知，

由于爷结点30位于非根结点的位置，所以把爷结点30染红，

此时满足红黑树的定义。

接下来要插入结点3，根据二叉排序树的插入规则可知结点3要插在结点5的左子树上，并把结点3涂红，

如下图：

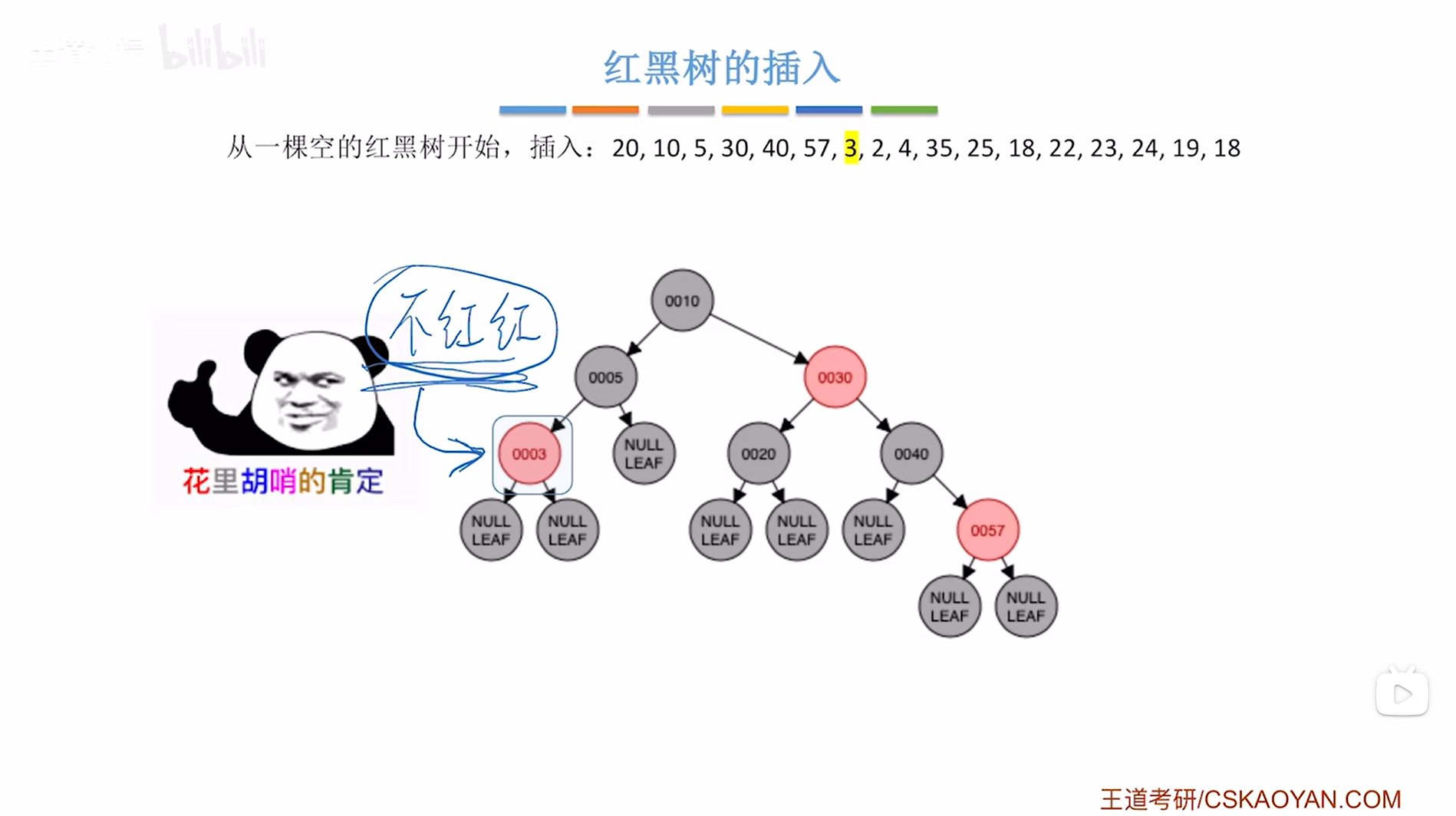
如上图，

此时满足红黑树的定义。

接下来要插入结点2，根据二叉排序树的插入规则可知结点2要插在结点3的左子树上，并把结点2涂红，

如下图：

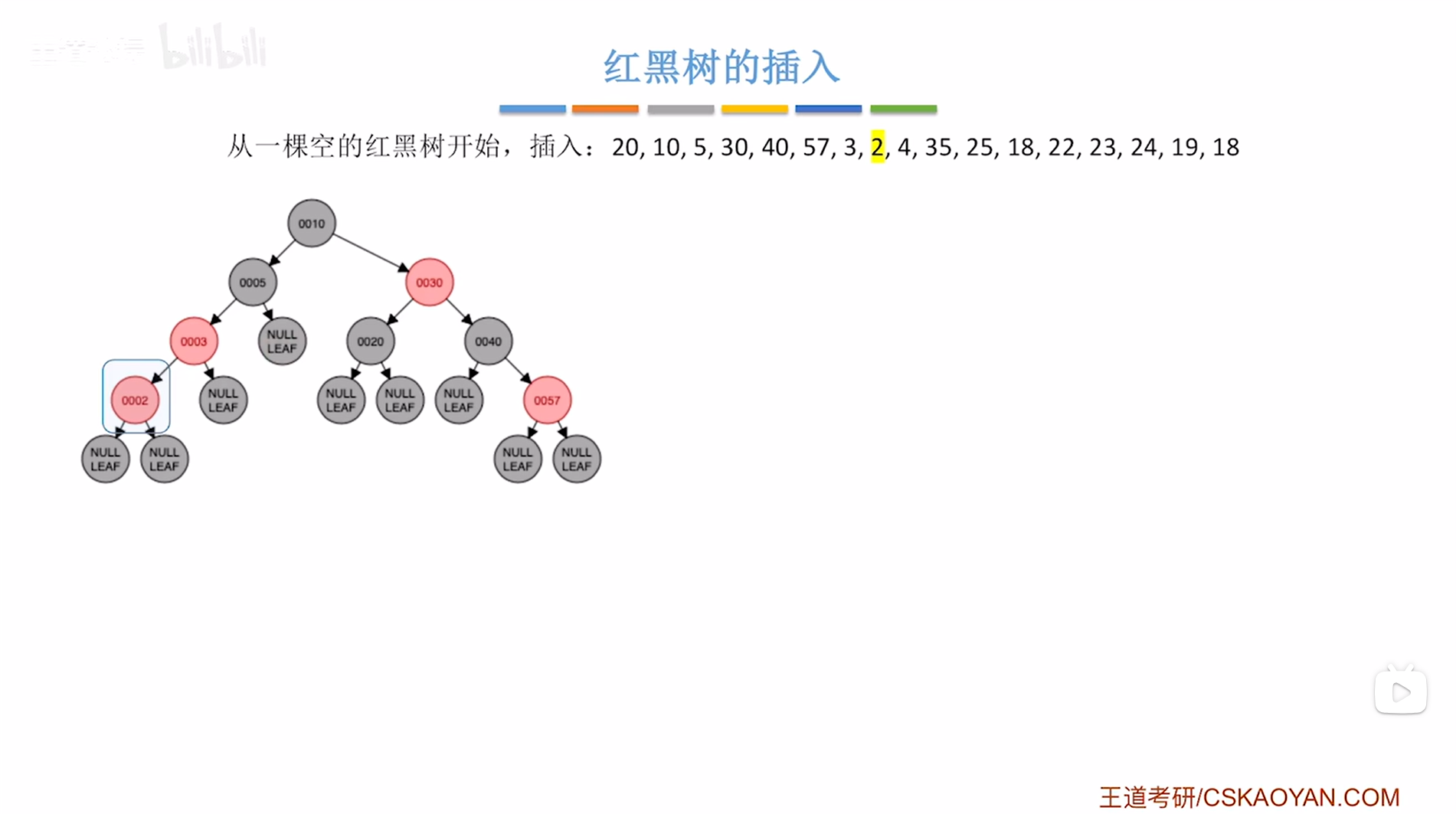
如上图，

此时结点2违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点2的叔叔结点的颜色，

结点2的父结点是3结点，3结点的兄弟结点是NULL LEAF结点(5结点的右孩子)，

所以结点2的叔叔结点是NULL LEAF结点(5结点的右孩子)，NULL LEAF结点(5结点的右孩子)是黑色结点，

因此需要"旋转+染色"->

由于3结点的父结点是5结点，所以结点2的爷爷结点是5结点，

因此结点2属于LL型即"新插入的结点2位于它的爷爷结点5的左孩子的左子树上"，

对于LL型的处理方法首先要右单旋使得父换爷，再进行染色->每一次的旋转操作都会使得儿子变为爹，原来的爹变为儿子；染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

其中结点2的父结点是3，爷结点是5，

通过右单旋让父结点3替代爷结点5的位置，

结点5会变为结点3的儿子，且原本的爷结点5要放在结点3的右孩子上，因为要保证二叉排序树的特性"左<根<右"，

旋转之后还需要染色，对于染色，处理的仍旧是父结点3和爷结点5，

父结点3原本是红色，染色后为黑色，爷结点5原本是黑色，染色后为红色，

如下图：

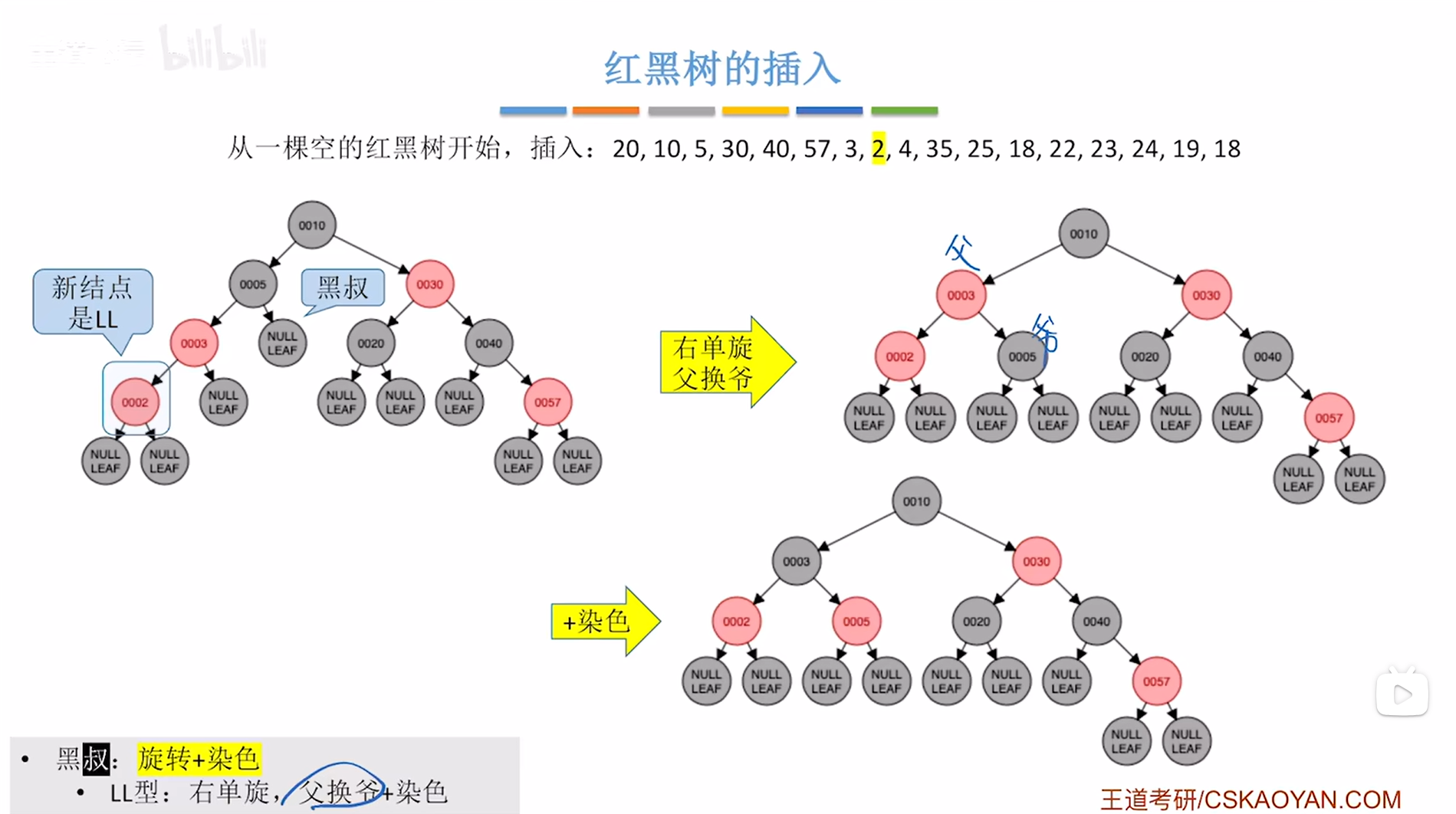
如上图，

此时满足红黑树的定义。

接下来要插入结点4，根据二叉排序树的插入规则可知结点4要插在结点5的左子树上，并把结点2涂红，

如下图：

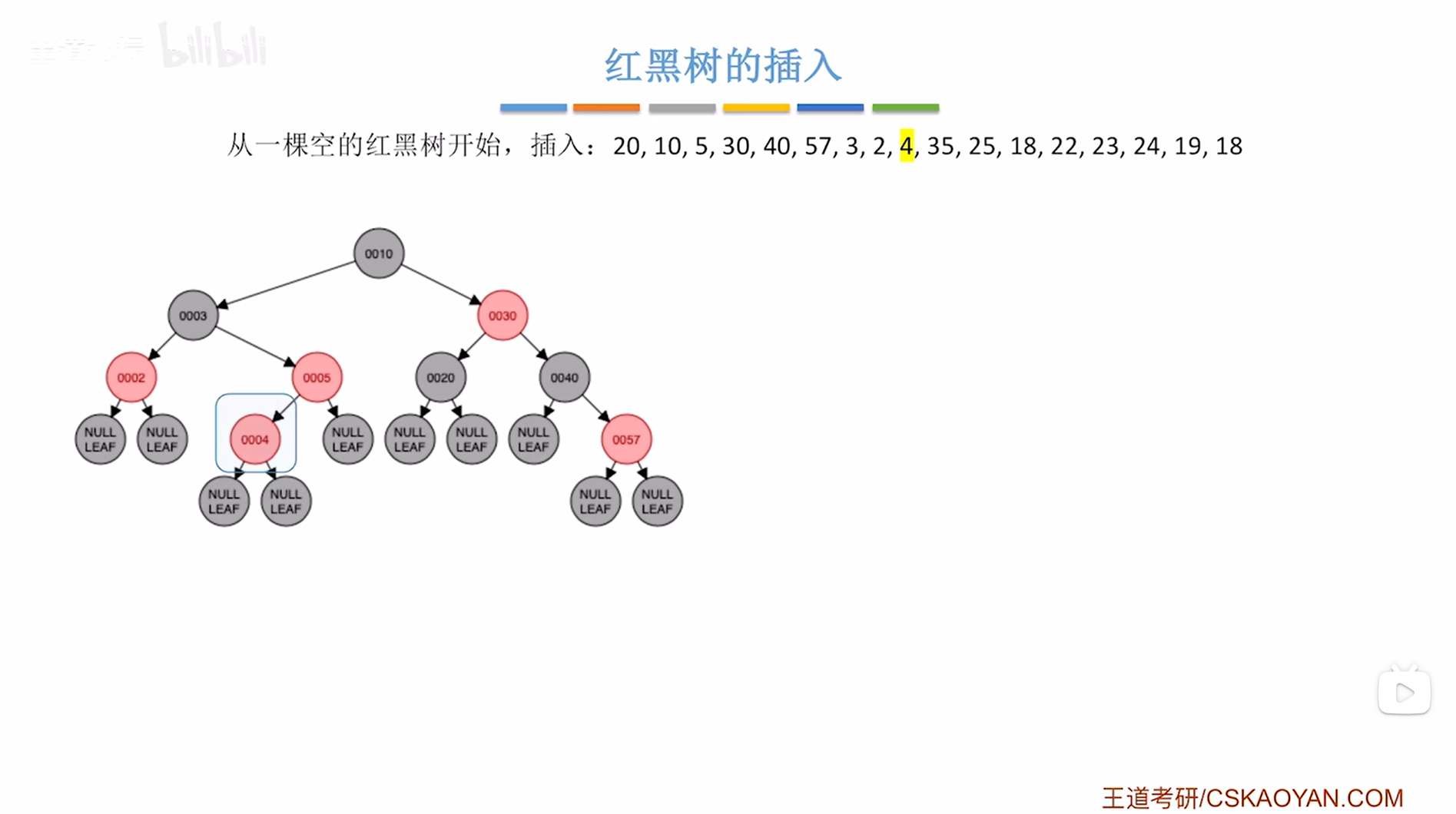
如上图，

此时结点4违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点4的叔叔结点的颜色，

结点4的父结点是5结点，5结点的兄弟结点是2结点，

所以结点4的叔叔结点是2结点，2结点是红色结点，

因此需要"染色+变新"即叔父爷染色，爷变为新结点->

首先"叔父爷染色"，其中新插入的结点4的叔结点是2结点、父结点是5结点、爷结点是3结点，

进行叔父爷染色，染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

如下图：

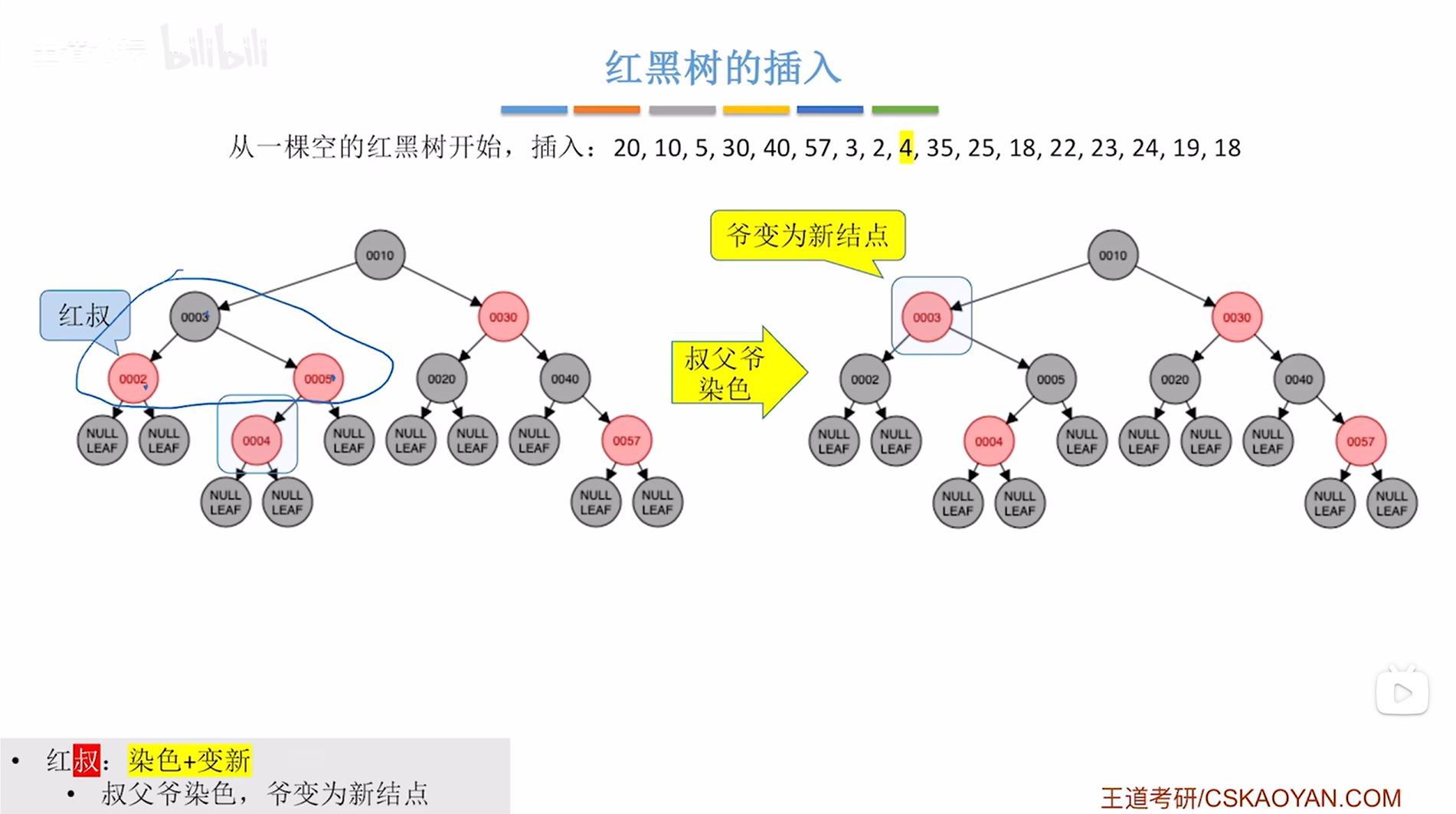
如上图，

再进行"爷变为新结点"，这一步针对于新插入的结点4的爷结点3，

这里要把爷结点3看作新插入的结点，再做调整，

根据"如果新结点是根结点，那么染为黑色；新结点非根，那么染为红色"可知，

由于爷结点3位于非根结点的位置，所以把爷结点3染红，

现在新插入的结点是结点3，结点3是非根结点，所以只需要判断是否破坏"不红红"，显然没有破坏，

此时满足红黑树的定义。

接下来要插入结点35，根据二叉排序树的插入规则可知结点35要插在结点40的左子树上，并把结点35涂红，

如下图：

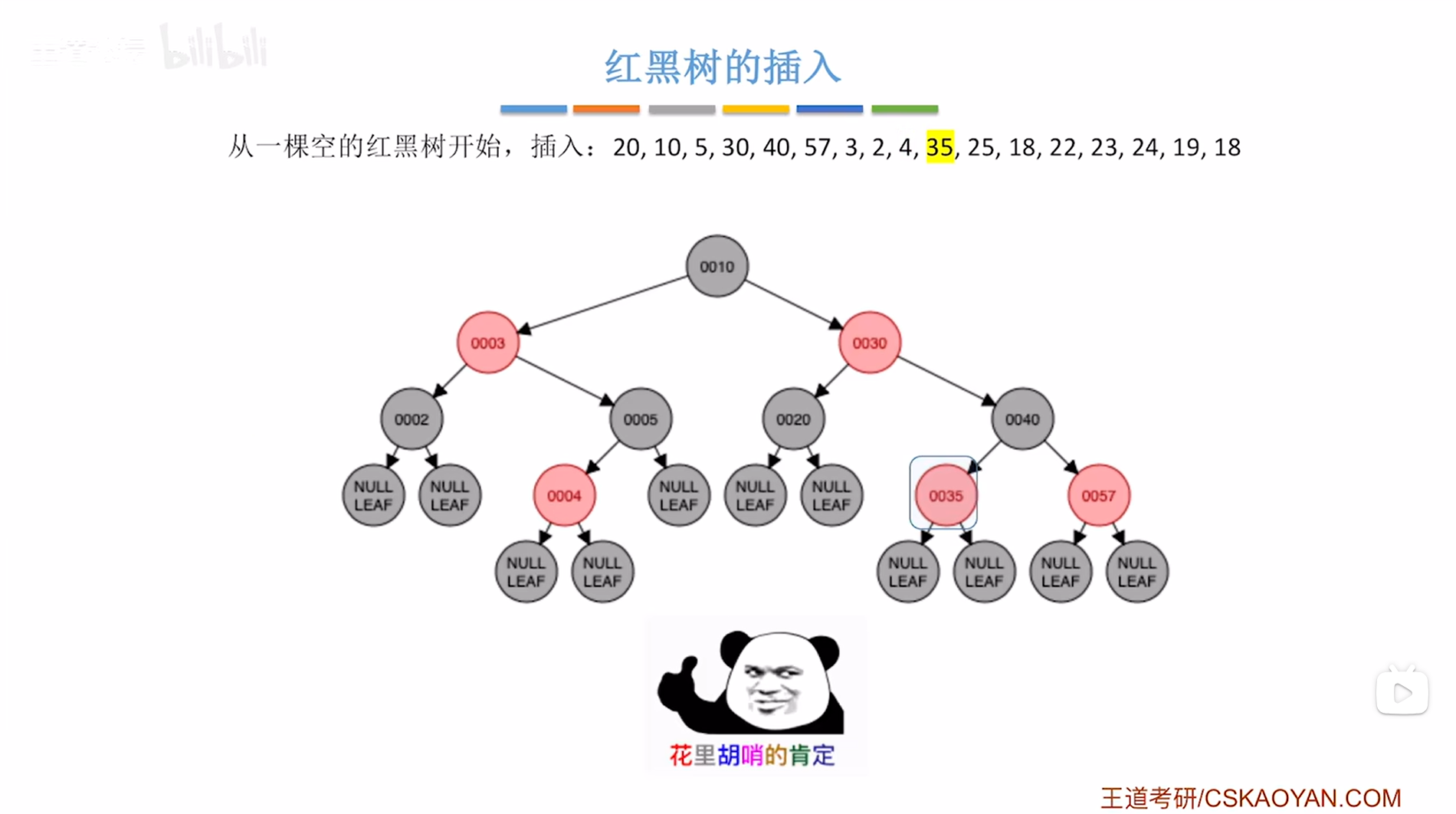
如上图，

新插入的结点是结点35，结点35是非根结点，所以只需要判断是否破坏"不红红"，显然没有破坏，

此时满足红黑树的定义。

接下来要插入结点25，根据二叉排序树的插入规则可知结点25要插在结点20的右子树上，并把结点25涂红，

如下图：

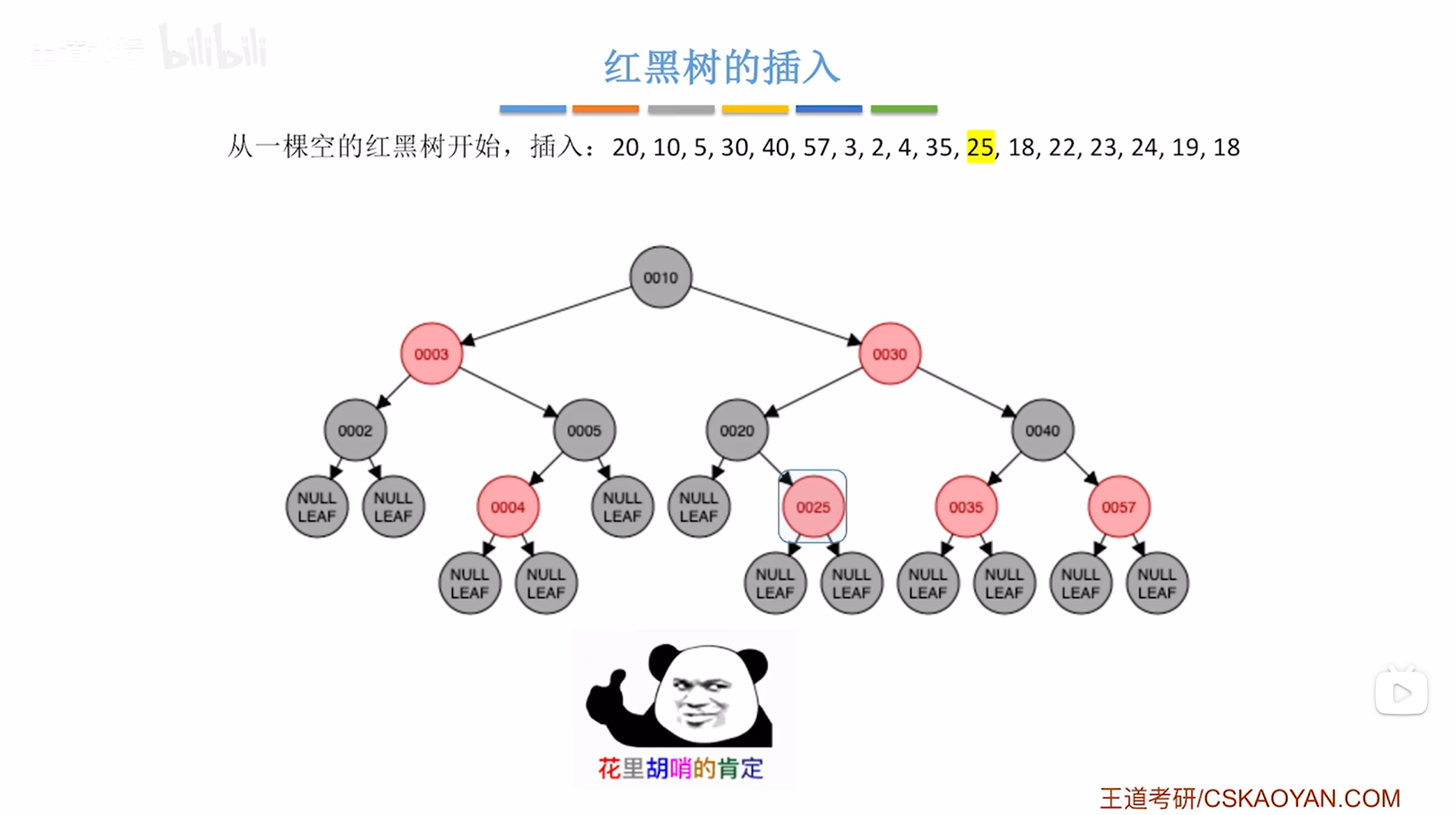
如上图，

新插入的结点是结点25，结点25是非根结点，所以只需要判断是否破坏"不红红"，显然没有破坏，

此时满足红黑树的定义。

接下来要插入结点18，根据二叉排序树的插入规则可知结点18要插在结点20的左子树上，并把结点18涂红，

如下图：

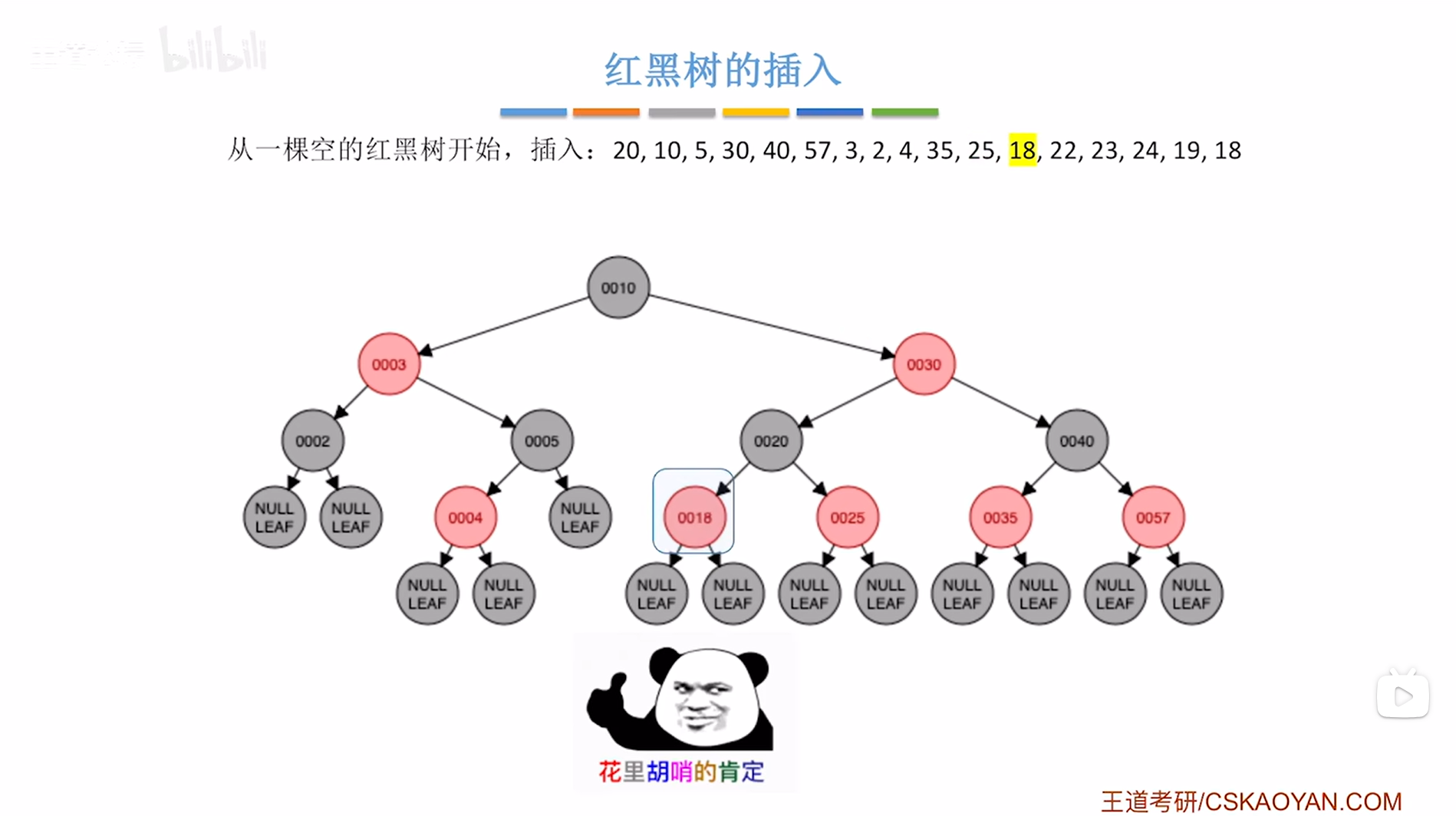
如上图，

新插入的结点是结点18，结点18是非根结点，所以只需要判断是否破坏"不红红"，显然没有破坏，

此时满足红黑树的定义。

->现在可以发现，当红黑树越来越大时，很多时候的插入都不需要进行调整。

接下来要插入结点22，根据二叉排序树的插入规则可知结点22要插在结点25的左子树上，并把结点22涂红，

如下图：

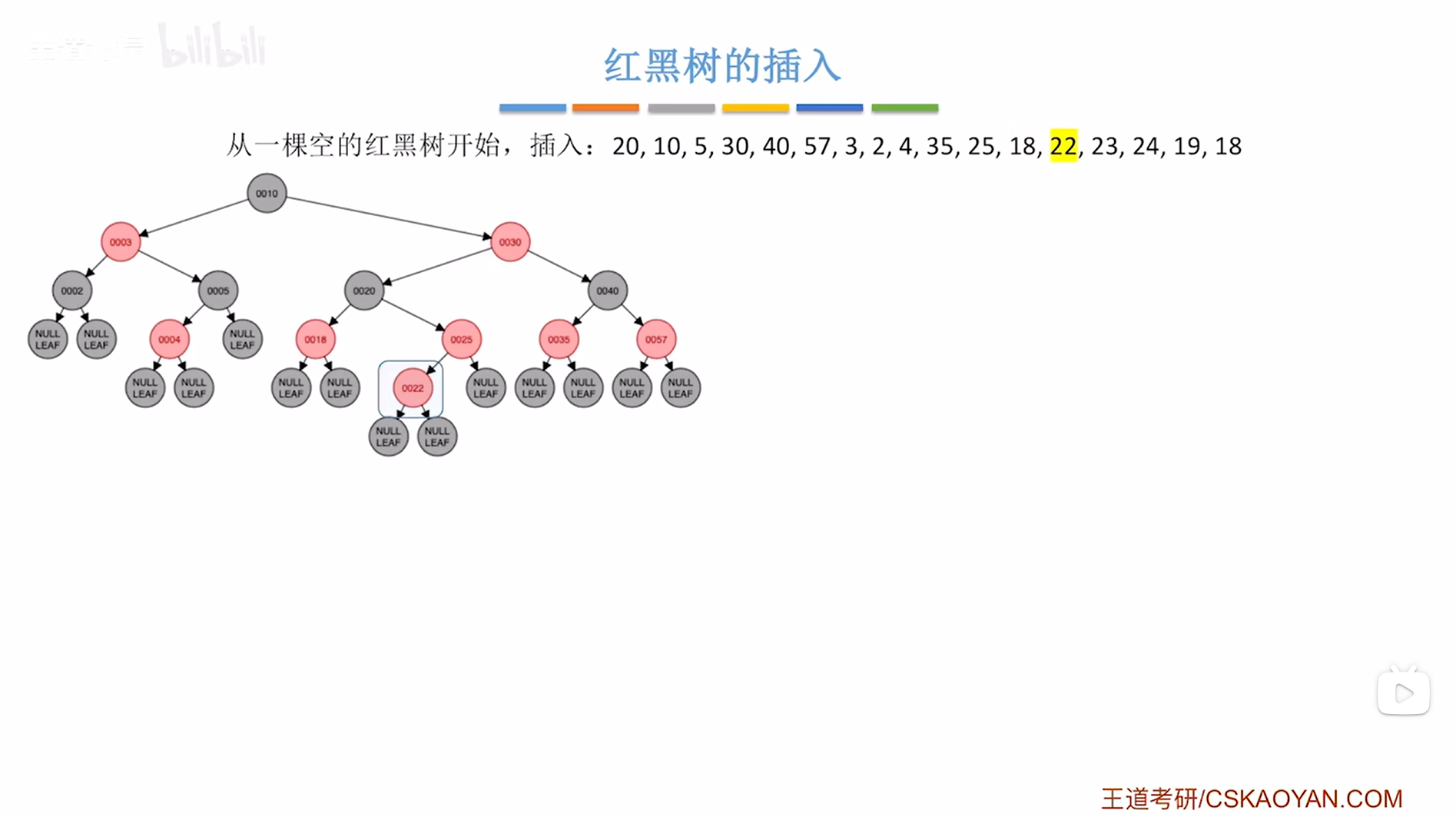
如上图，

此时结点22违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点22的叔叔结点的颜色，

结点22的父结点是25结点，25结点的兄弟结点是18结点，

所以结点22的叔叔结点是18结点，18结点是红色结点，

因此需要"染色+变新"即叔父爷染色，爷变为新结点->

首先"叔父爷染色"，其中新插入的结点22的叔结点是18结点、父结点是25结点、爷结点是20结点，

进行叔父爷染色，染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

如下图：

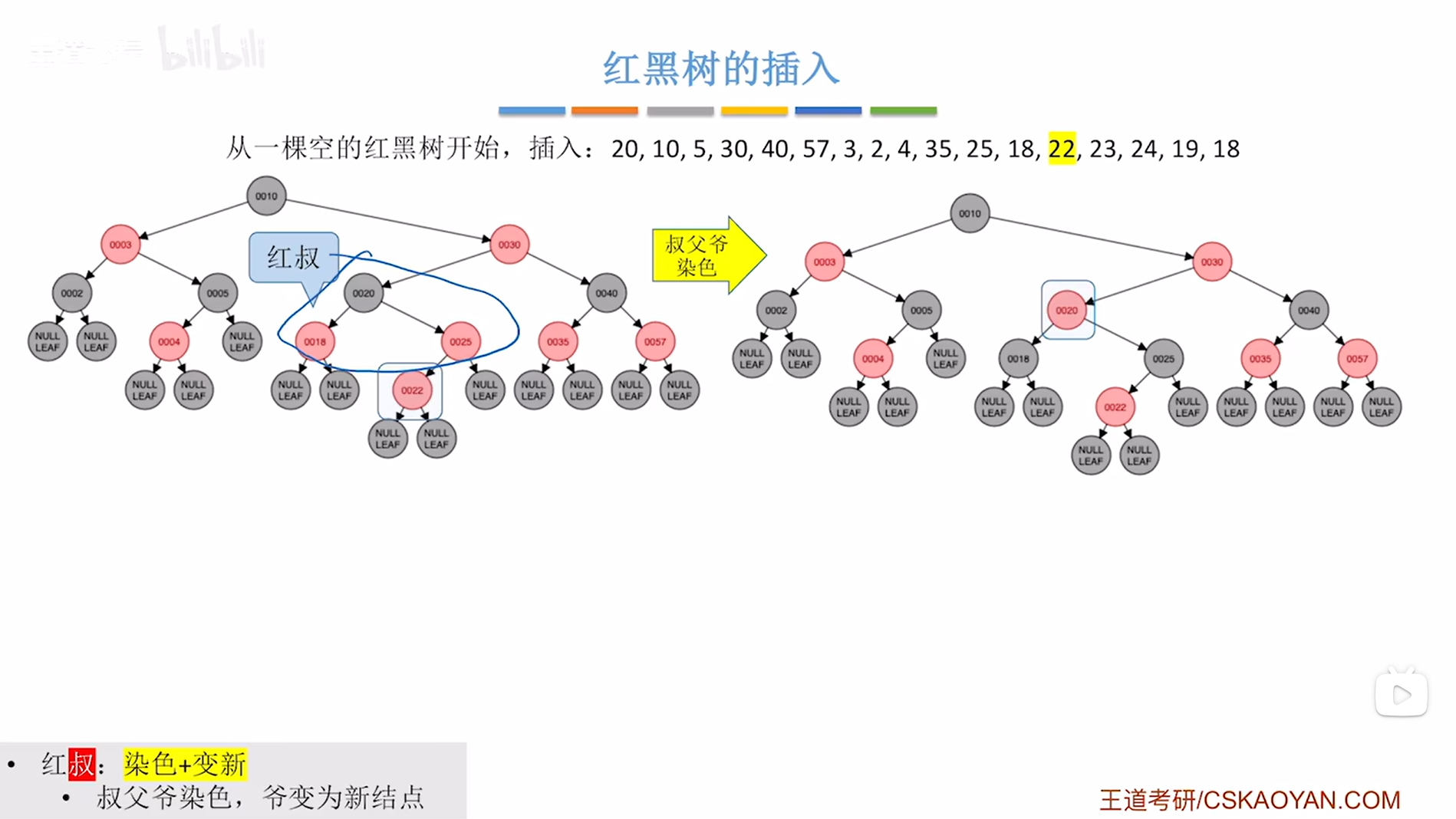
如上图，

再进行"爷变为新结点"，这一步针对于新插入的结点22的爷结点20，

这里要把爷结点20看作新插入的结点，再做调整，

根据"如果新结点是根结点，那么染为黑色；新结点非根，那么染为红色"可知，

由于爷结点20位于非根结点的位置，所以把爷结点20染红，

现在新插入的结点是结点20，结点20是非根结点，所以只需要判断是否破坏"不红红"，显然破坏了，

如下图：

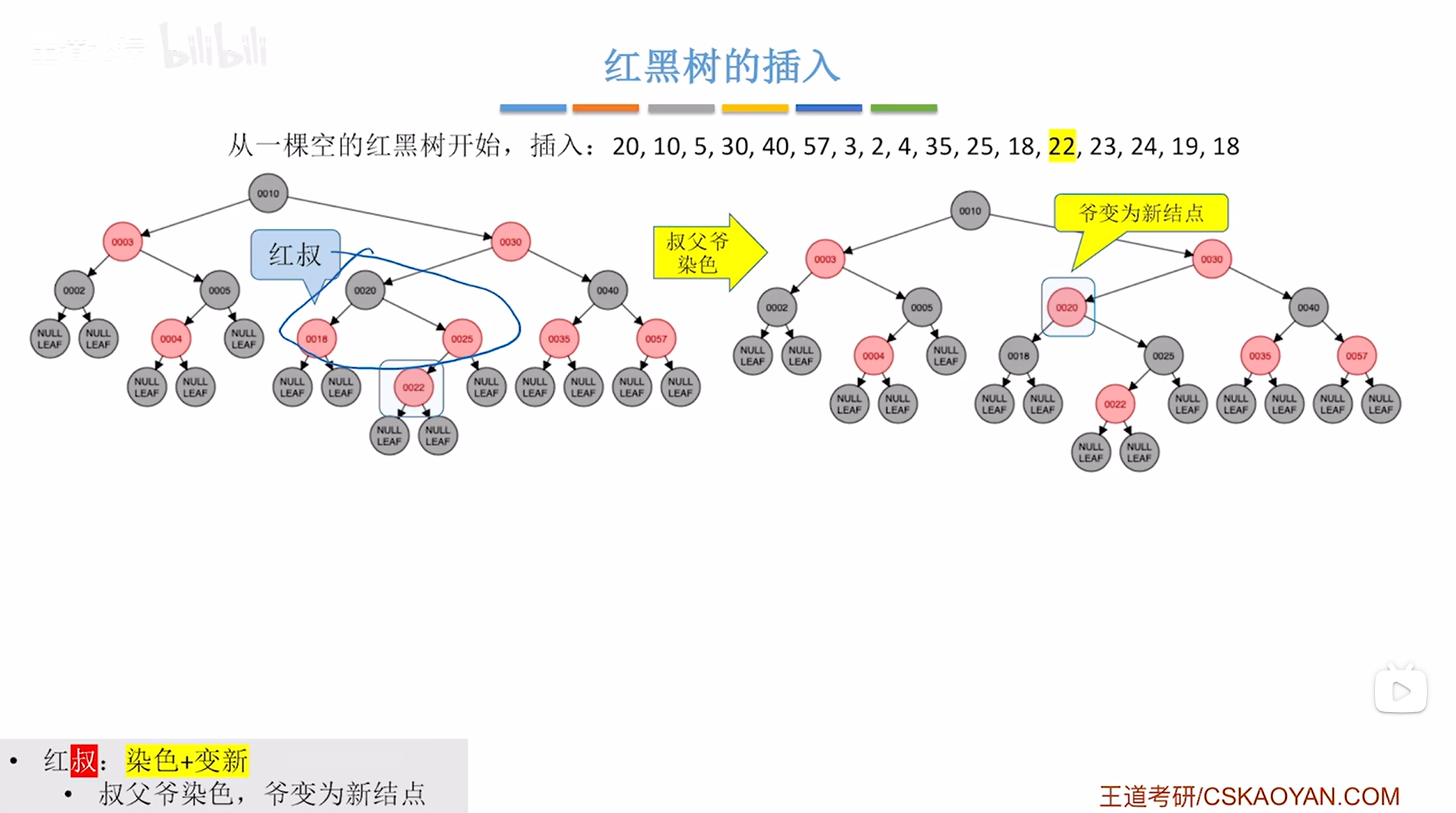
如上图，

此时结点20违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点20的叔叔结点的颜色，

结点20的父结点是30结点，30结点的兄弟结点是3结点，

所以结点20的叔叔结点是3结点，3结点是红色结点，

因此需要"染色+变新"即叔父爷染色，爷变为新结点->

首先"叔父爷染色"，其中新插入的结点20的叔结点是3结点、父结点是30结点、爷结点是10结点，

进行叔父爷染色，染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

如下图：

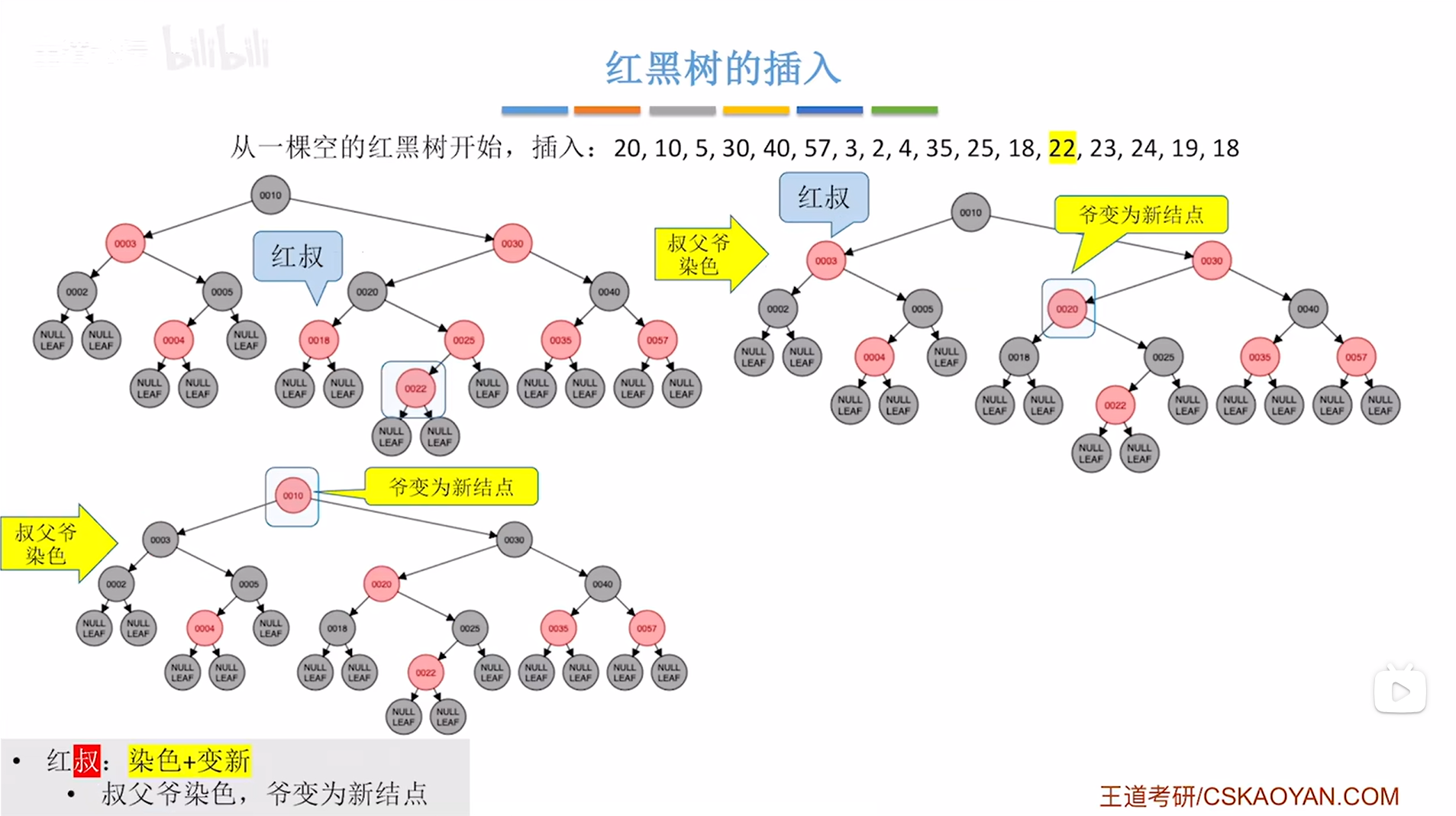
如上图，

再进行"爷变为新结点"，这一步针对于新插入的结点20的爷结点10，

这里要把爷结点10看作新插入的结点，再做调整，

根据"如果新结点是根结点，那么染为黑色；新结点非根，那么染为红色"可知，

由于爷结点10位于根结点的位置，所以把爷结点10染黑，

此时满足红黑树的定义。

如下图：

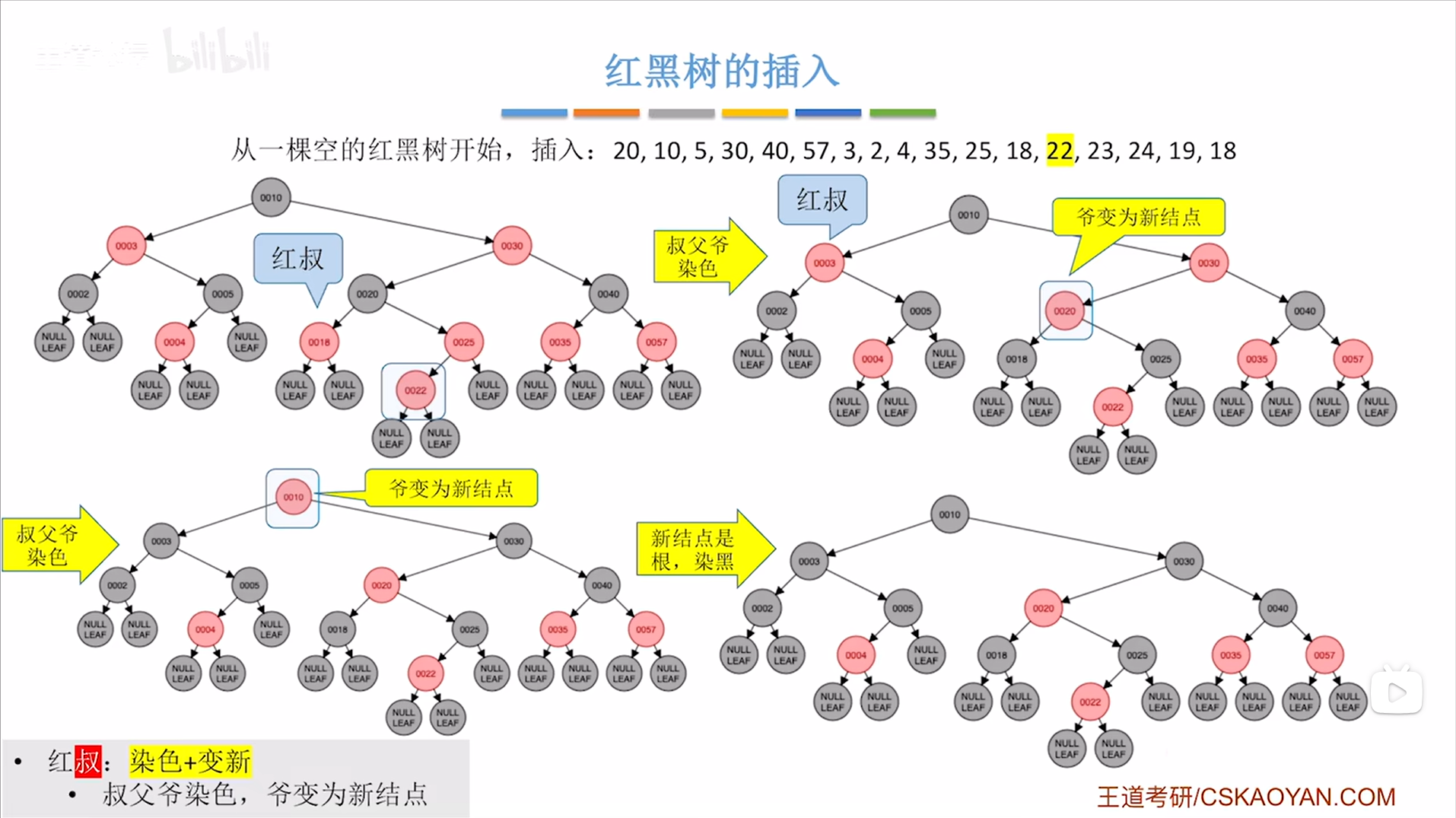
如上图，

接下来要插入结点23，根据二叉排序树的插入规则可知结点23要插在结点22的右子树上，并把结点23涂红，

如下图：

如上图，

此时结点23违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点23的叔叔结点的颜色，

结点23的父结点是22结点，22结点的兄弟结点是NULL LEAF结点(25结点的右孩子)，

所以结点23的叔叔结点是NULL LEAF结点(25结点的右孩子)，NULL LEAF结点(25结点的右孩子)是黑色结点，

因此需要"旋转+染色"->

由于22结点的父结点是25结点，所以结点23的爷爷结点是25结点，

因此结点23属于LR型即"新插入的结点23位于它的爷爷结点25的左孩子的右子树上"，

对于LR型的处理方法要先左旋，再右旋使得儿换爷，最后进行染色->关键是把儿结点换到爷结点的位置，新插入的结点就是儿子结点，先通过左旋换到父结点的位置，再通过右旋换到爷结点的位置；染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

其中结点23的父结点是22，爷结点是25，

通过左旋让结点23换到父结点22的位置，由于父结点22小于结点23，所以父结点22要挂在结点23的左子树上（要保证二叉排序树的特性"左<根<右"），

如下图：

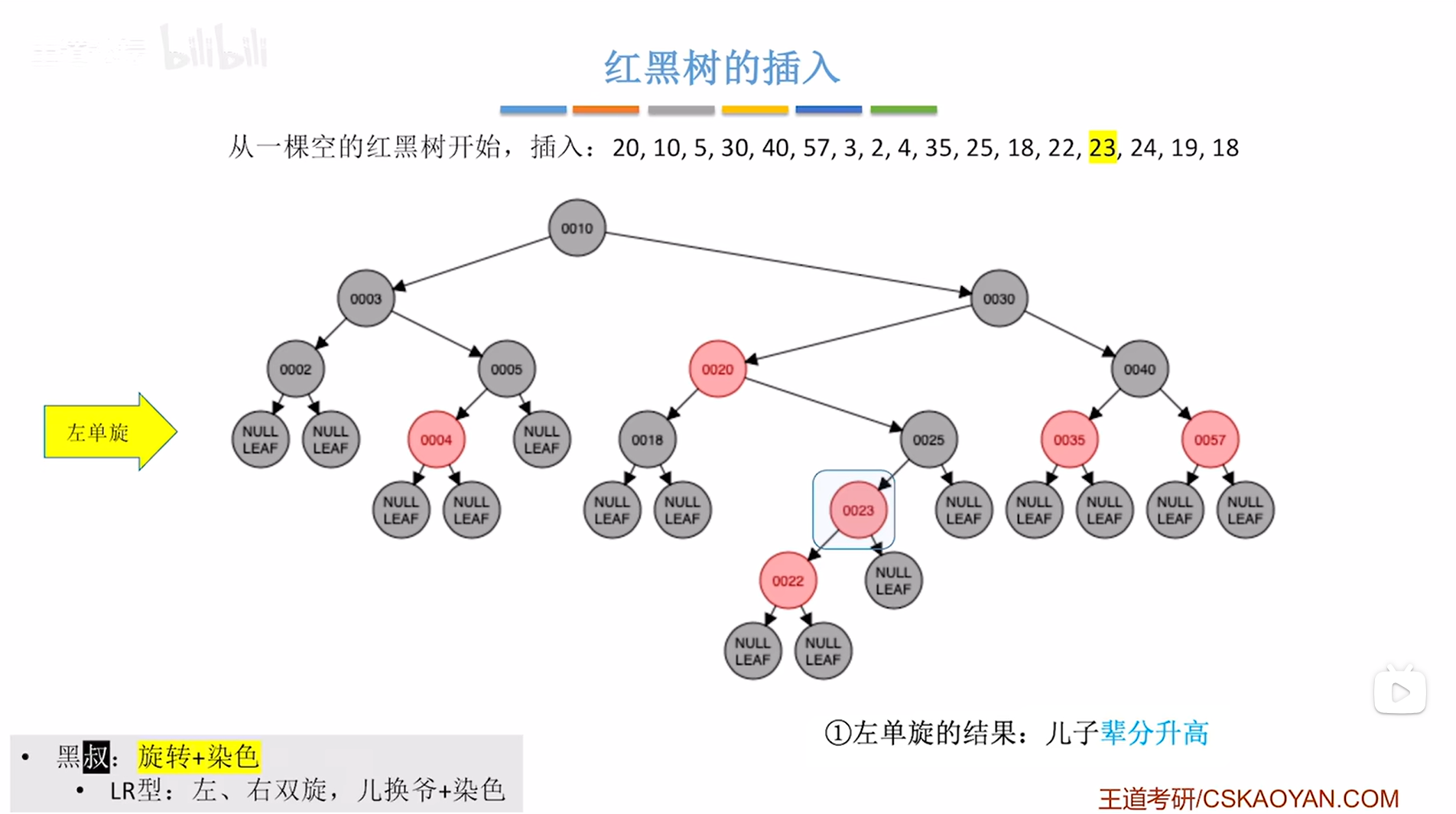
如上图，

再通过右旋把结点23换到爷结点25的位置，由于爷结点25大于结点23，所以爷结点25要挂在结点23的右子树上（要保证二叉排序树的特性"左<根<右"），

如下图：

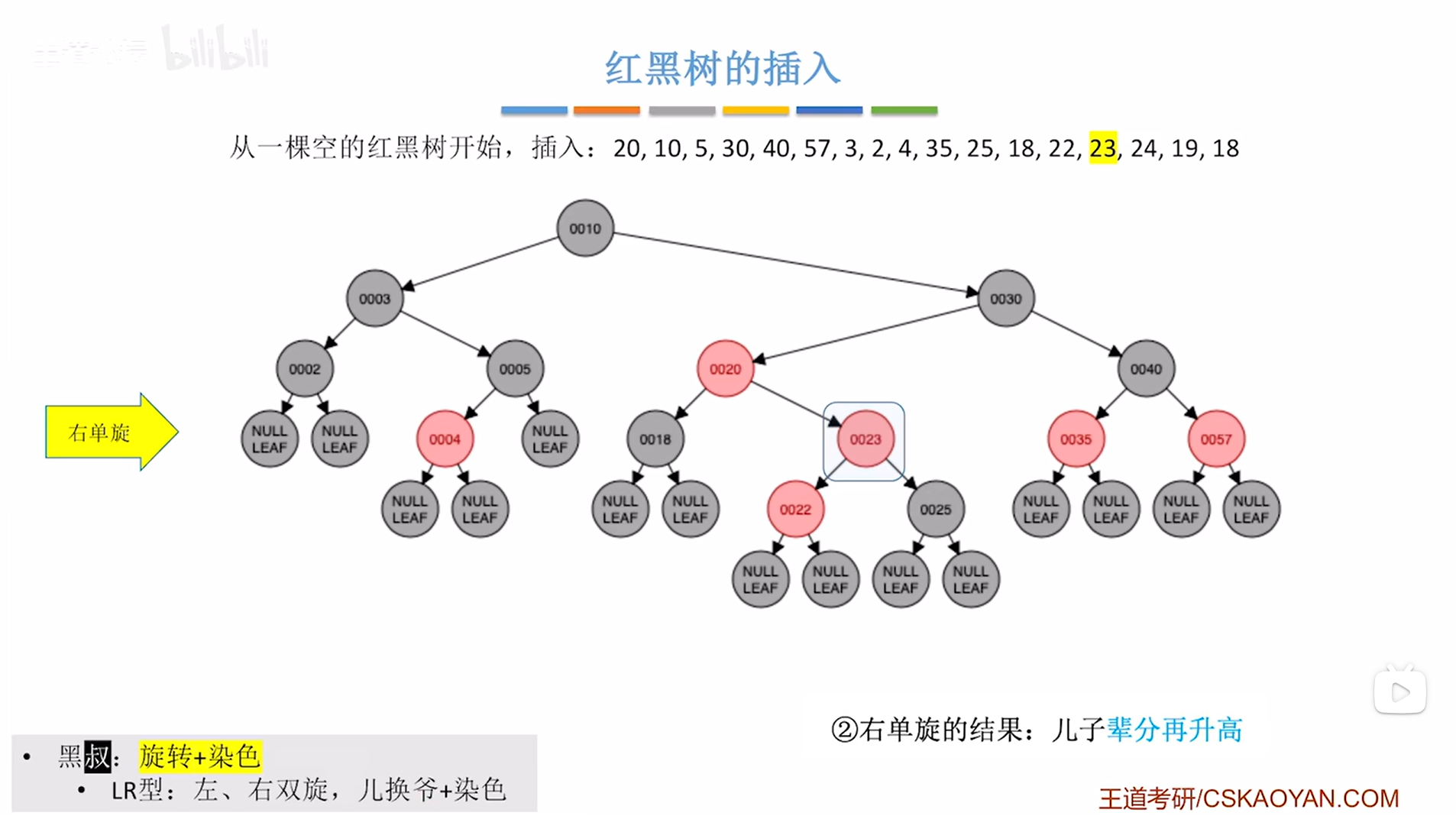
如上图，

旋转之后还需要染色，对于染色，处理的是儿子结点23和爷结点25，

儿子结点23原本是红色，染色后为黑色，爷结点25原本是黑色，染色后为红色，

如下图：

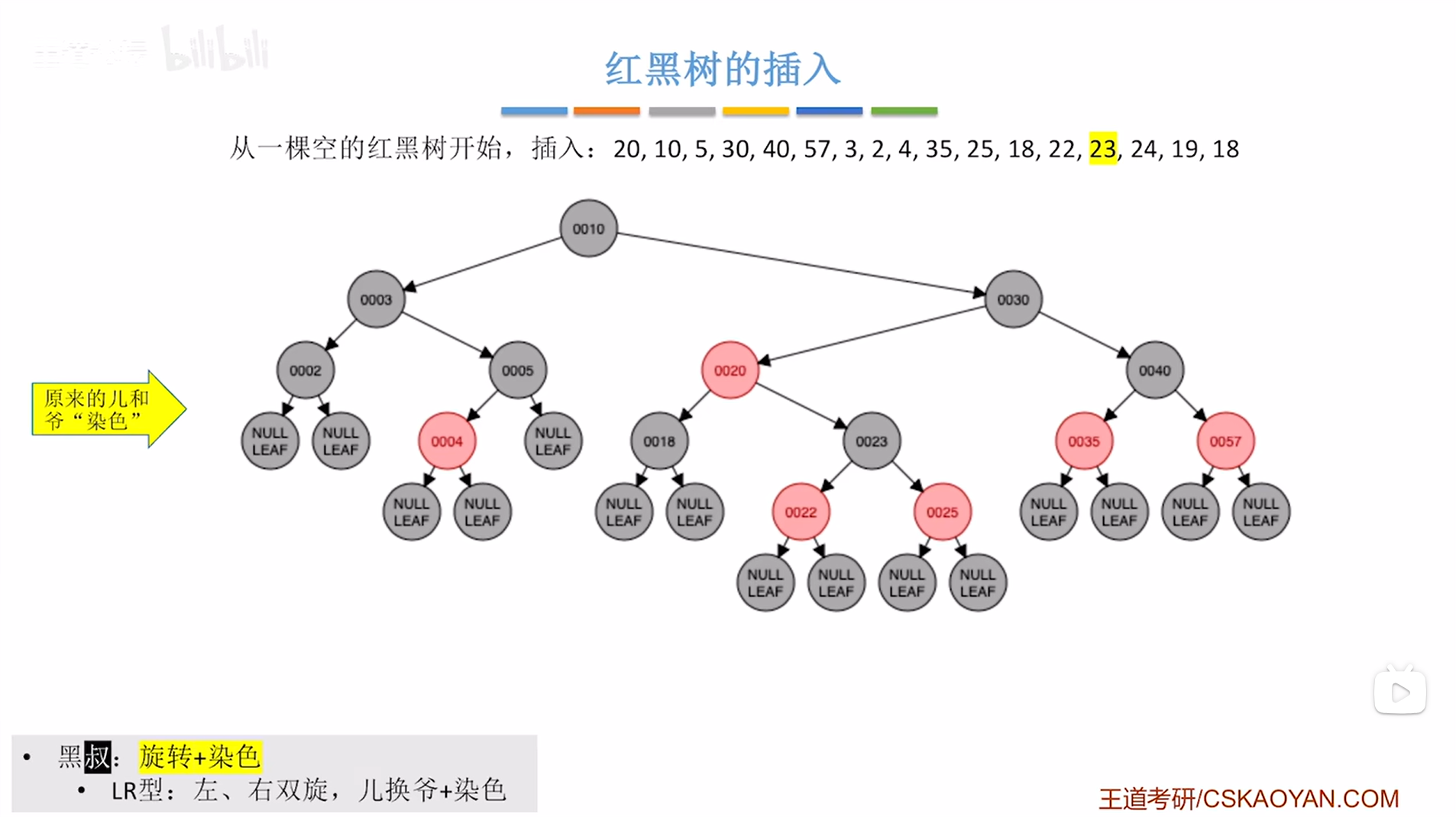
如上图，

此时满足红黑树的定义。

接下来要插入结点24，根据二叉排序树的插入规则可知结点24要插在结点25的左子树上，并把结点24涂红，

如下图：

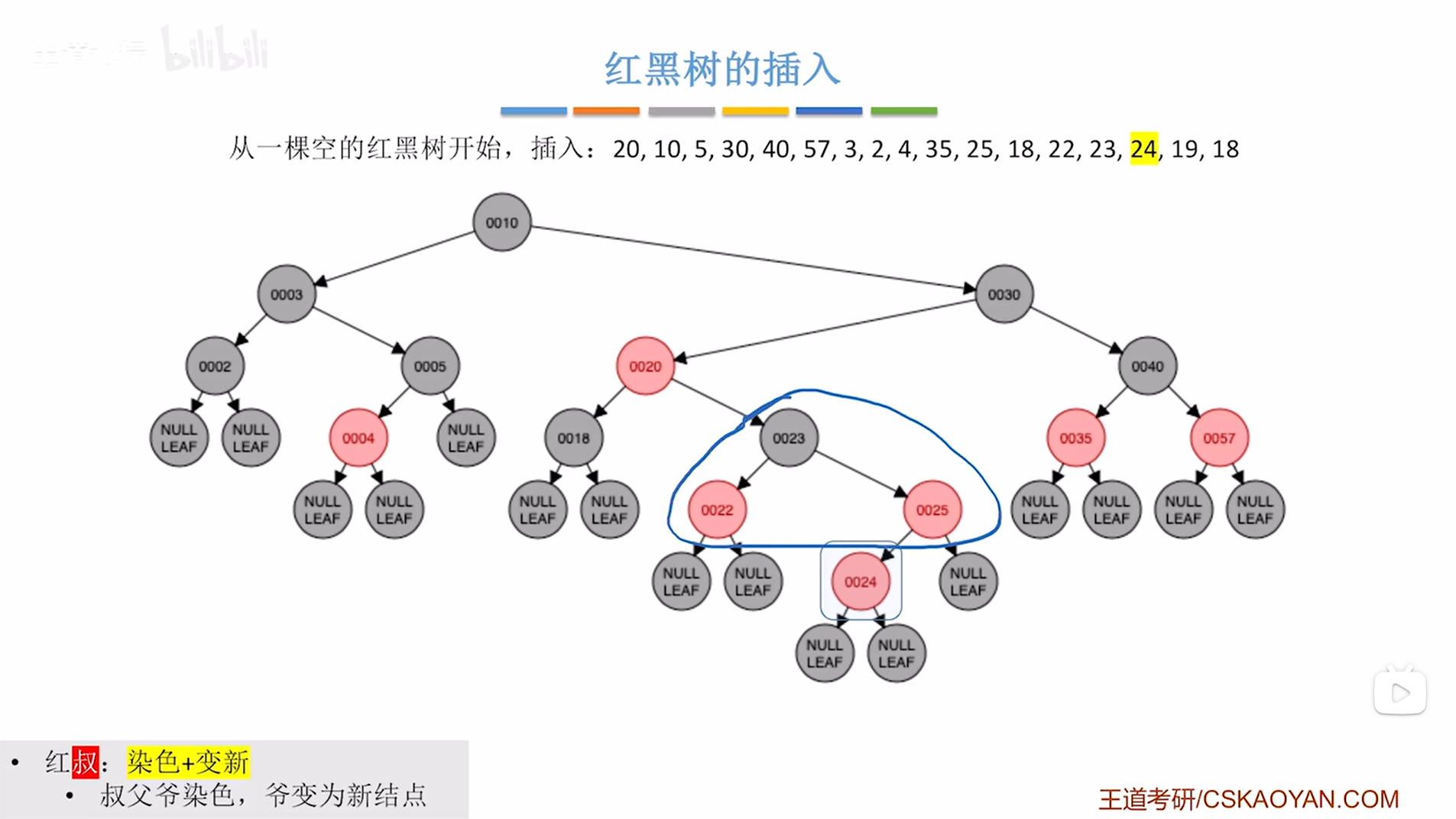
如上图，

此时结点24违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点24的叔叔结点的颜色，

结点24的父结点是25结点，25结点的兄弟结点是22结点，

所以结点24的叔叔结点是22结点，22结点是红色结点，

因此需要"染色+变新"即叔父爷染色，爷变为新结点->

首先"叔父爷染色"，其中新插入的结点24的叔结点是22结点、父结点是25结点、爷结点是23结点，

进行叔父爷染色，染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

如下图：

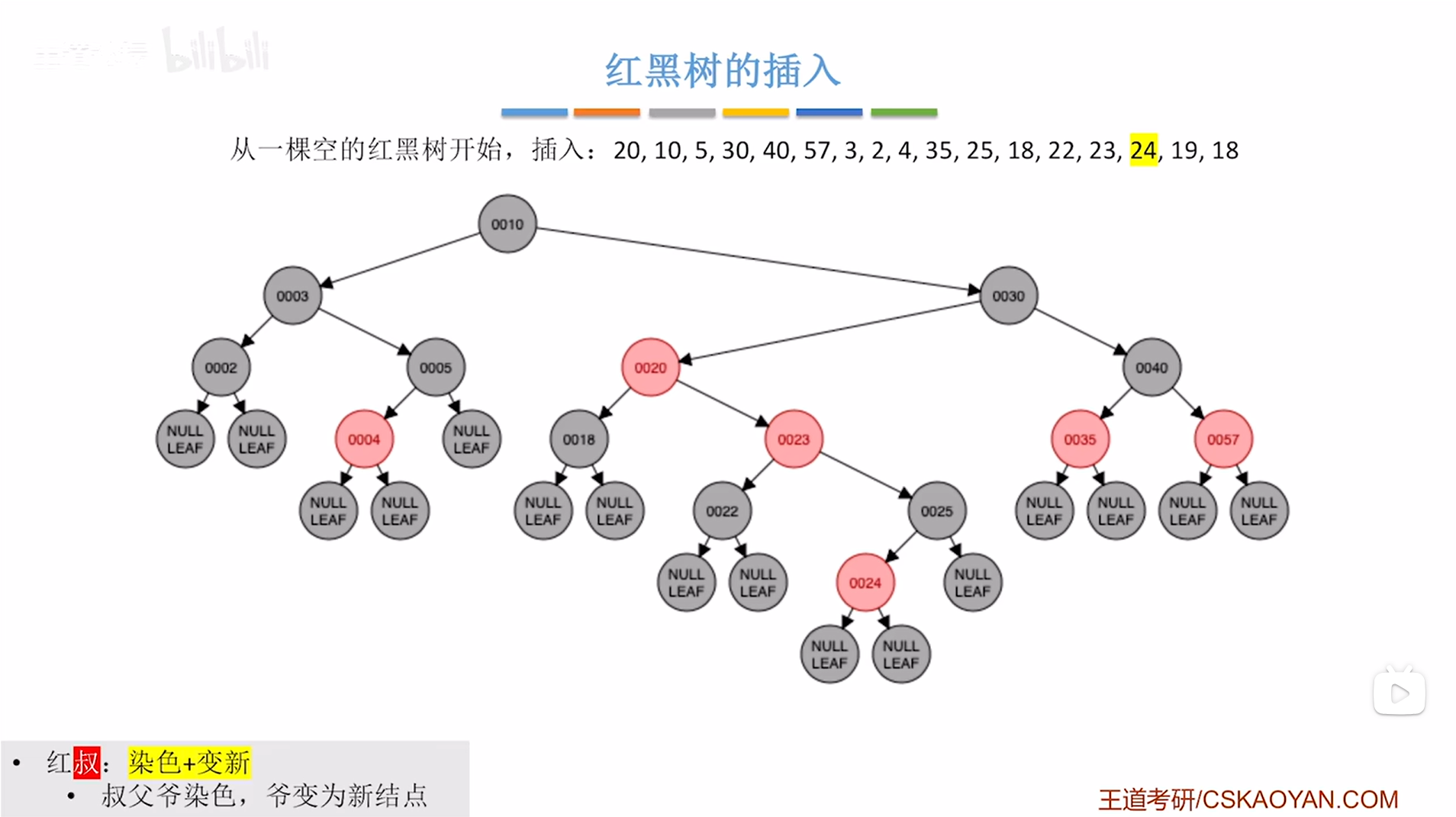
如上图，

再进行"爷变为新结点"，这一步针对于新插入的结点24的爷结点23，

这里要把爷结点23看作新插入的结点，再做调整，

根据"如果新结点是根结点，那么染为黑色；新结点非根，那么染为红色"可知，

由于爷结点23位于非根结点的位置，所以把爷结点23染红，

如下图：

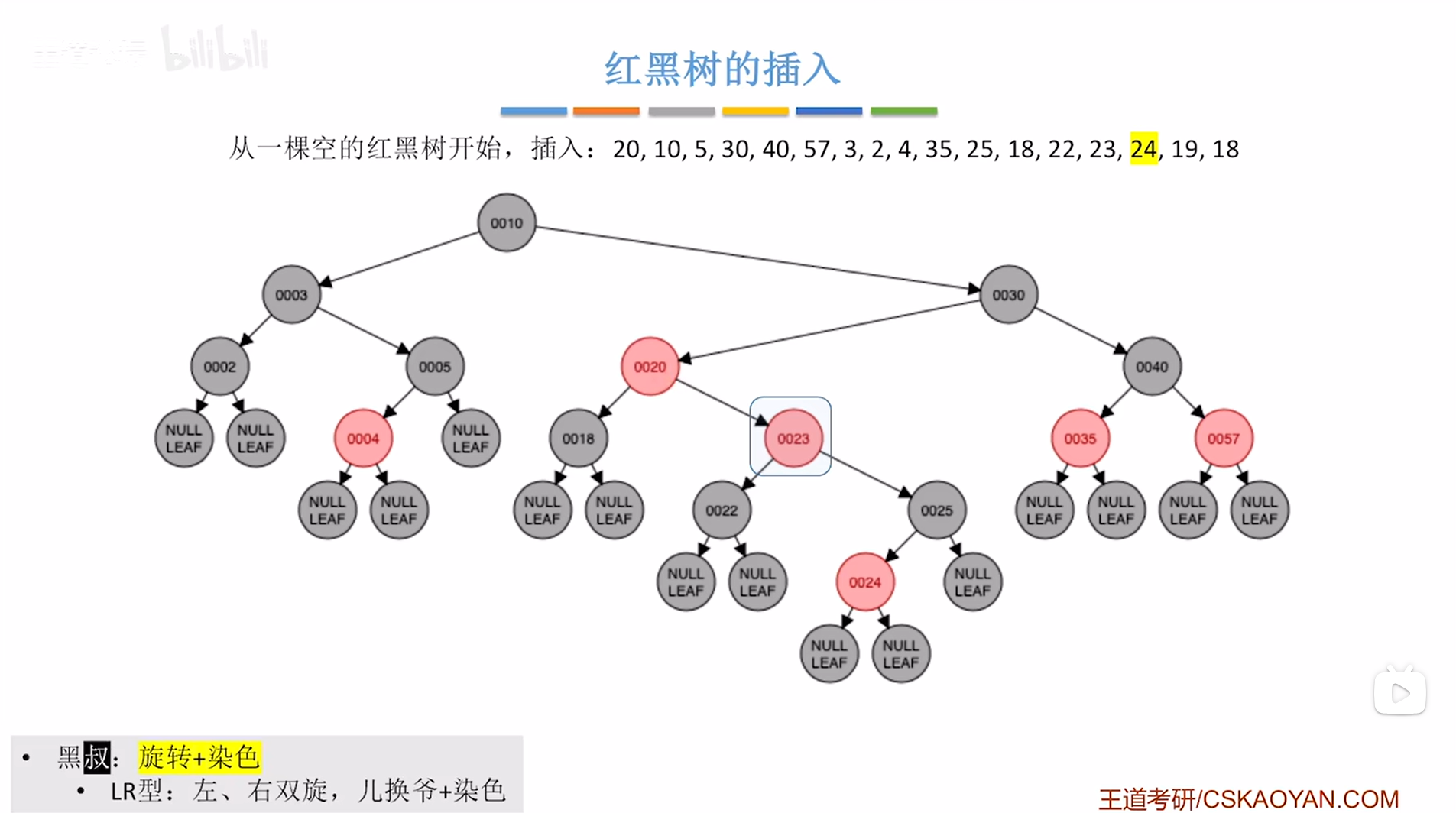
如上图，

此时结点23违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看结点23的叔叔结点的颜色，

结点23的父结点是20结点，20结点的兄弟结点是40结点，

所以结点23的叔叔结点是40结点，40结点是黑色结点，

因此需要"旋转+染色"->

由于20结点的父结点是30结点，所以结点23的爷爷结点是30结点，

因此结点23属于LR型即"新插入的结点23位于它的爷爷结点30的左孩子的右子树上"，

对于LR型的处理方法要先左旋，再右旋使得儿换爷，最后进行染色->关键是把儿结点换到爷结点的位置，新插入的结点就是儿子结点，先通过左旋换到父结点的位置，再通过右旋换到爷结点的位置；染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

其中结点23的父结点是20，爷结点是30，

通过左旋让结点23换到父结点20的位置，由于父结点20小于结点23，所以以父结点20为根结点的树要挂在结点23的左子树上（要保证二叉排序树的特性"左<根<右"），

23结点原来的左子树即以结点22为根结点的树就不能在23结点的左孩子上了，因为结点23的左孩子已经被占，由于结点22大于结点20，且结点20的右孩子为空，所以以结点22为根结点的树可以挂到结点20的右子树上，

如下图：

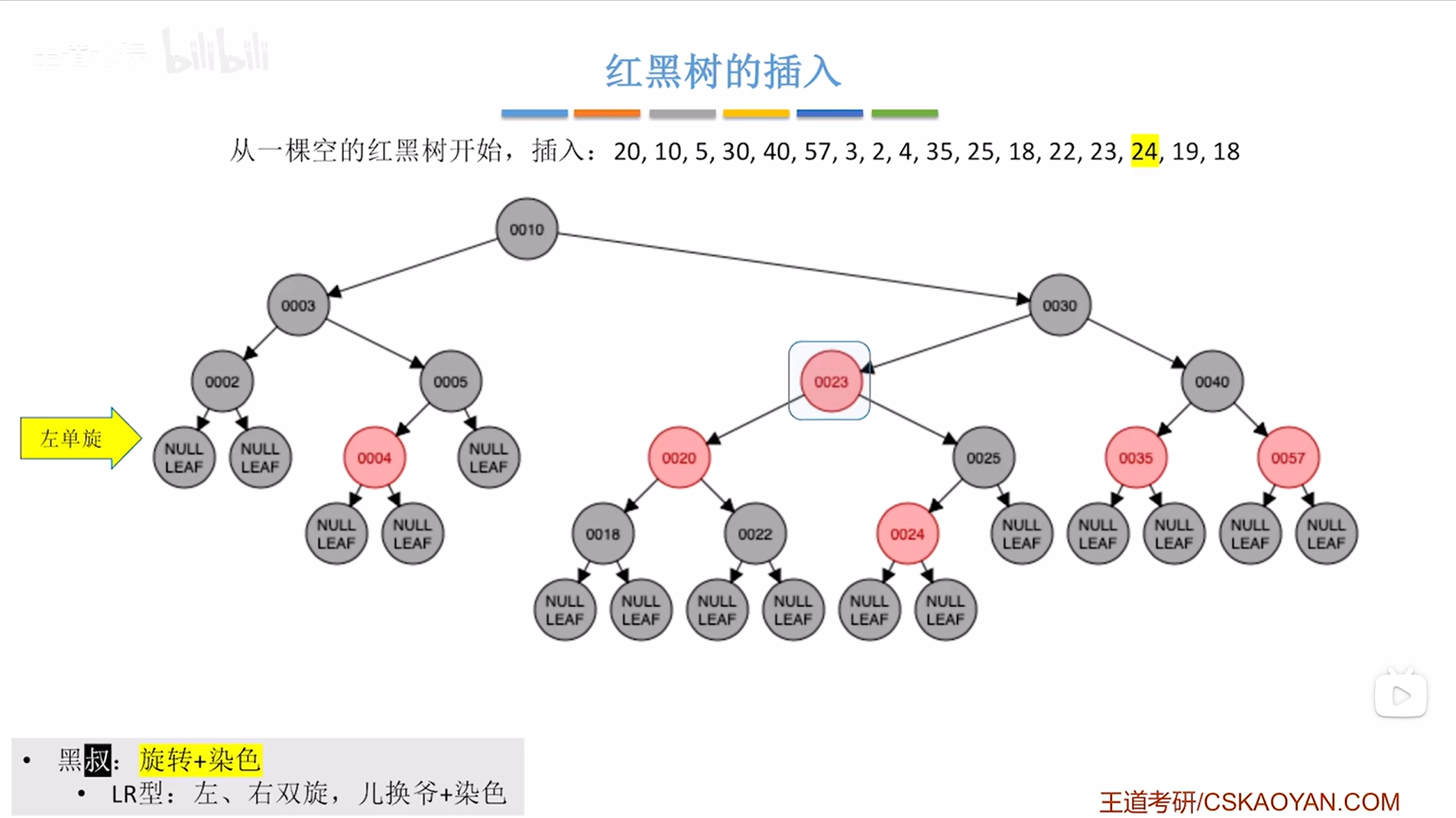
如上图，

再通过右旋把结点23换到爷结点30的位置，由于爷结点30大于结点23，所以爷结点30要挂在结点23的右子树上（要保证二叉排序树的特性"左<根<右"），

23结点原来的右子树即以结点25为根结点的树就不能在23结点的右孩子上了，因为结点23的右孩子已经被占，由于结点25小于结点30，且结点30的左孩子为空，所以以结点25为根结点的树可以挂到结点30的左子树上，

如下图：

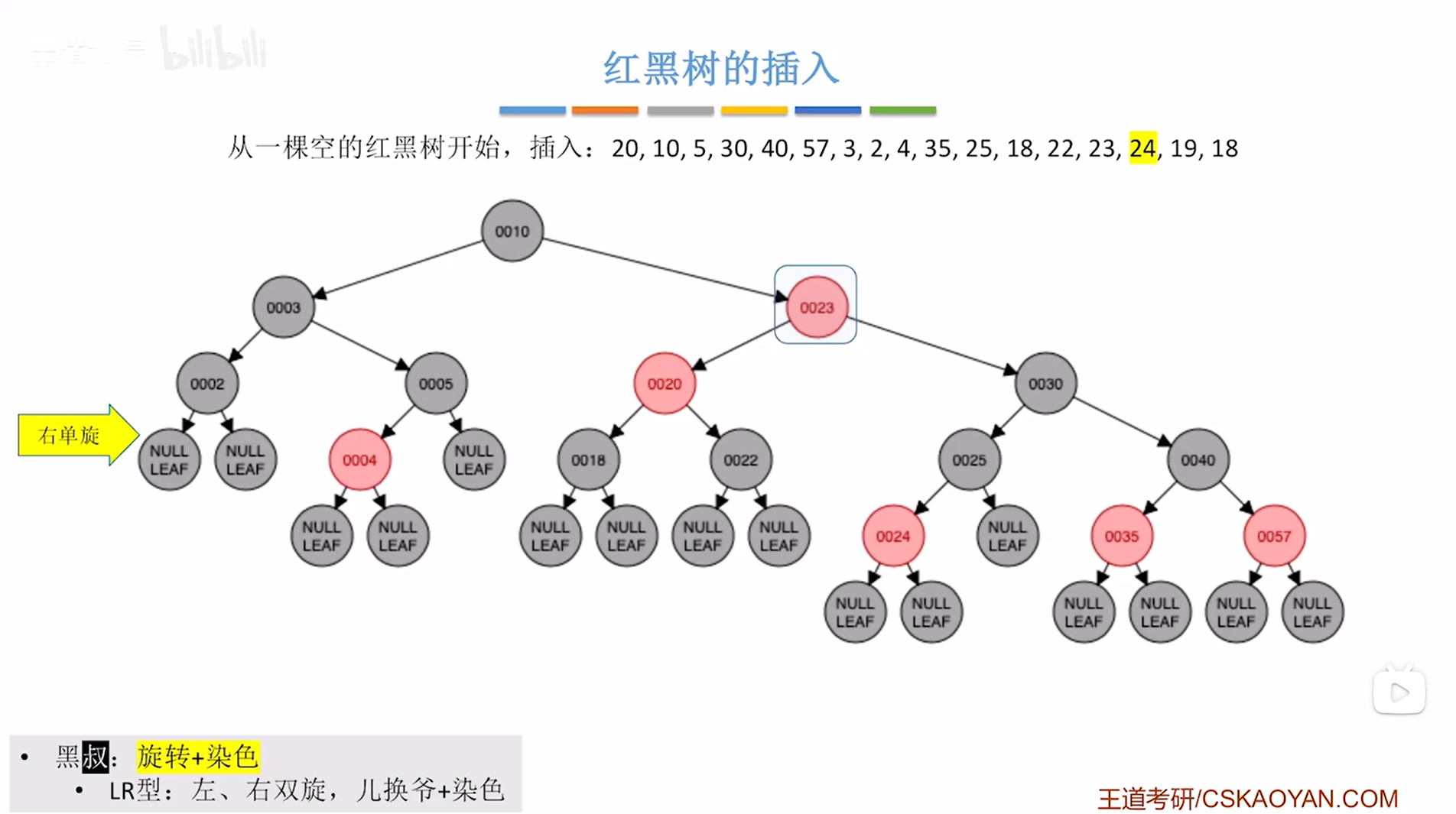
如上图，

旋转之后还需要染色，对于染色，处理的是儿子结点23和爷结点30，

儿子结点23原本是红色，染色后为黑色，爷结点30原本是黑色，染色后为红色，

如下图：

如上图，

此时满足红黑树的定义。

接下来要插入结点19，根据二叉排序树的插入规则可知结点19要插在结点18的右子树上，并把结点19涂红，

如下图：

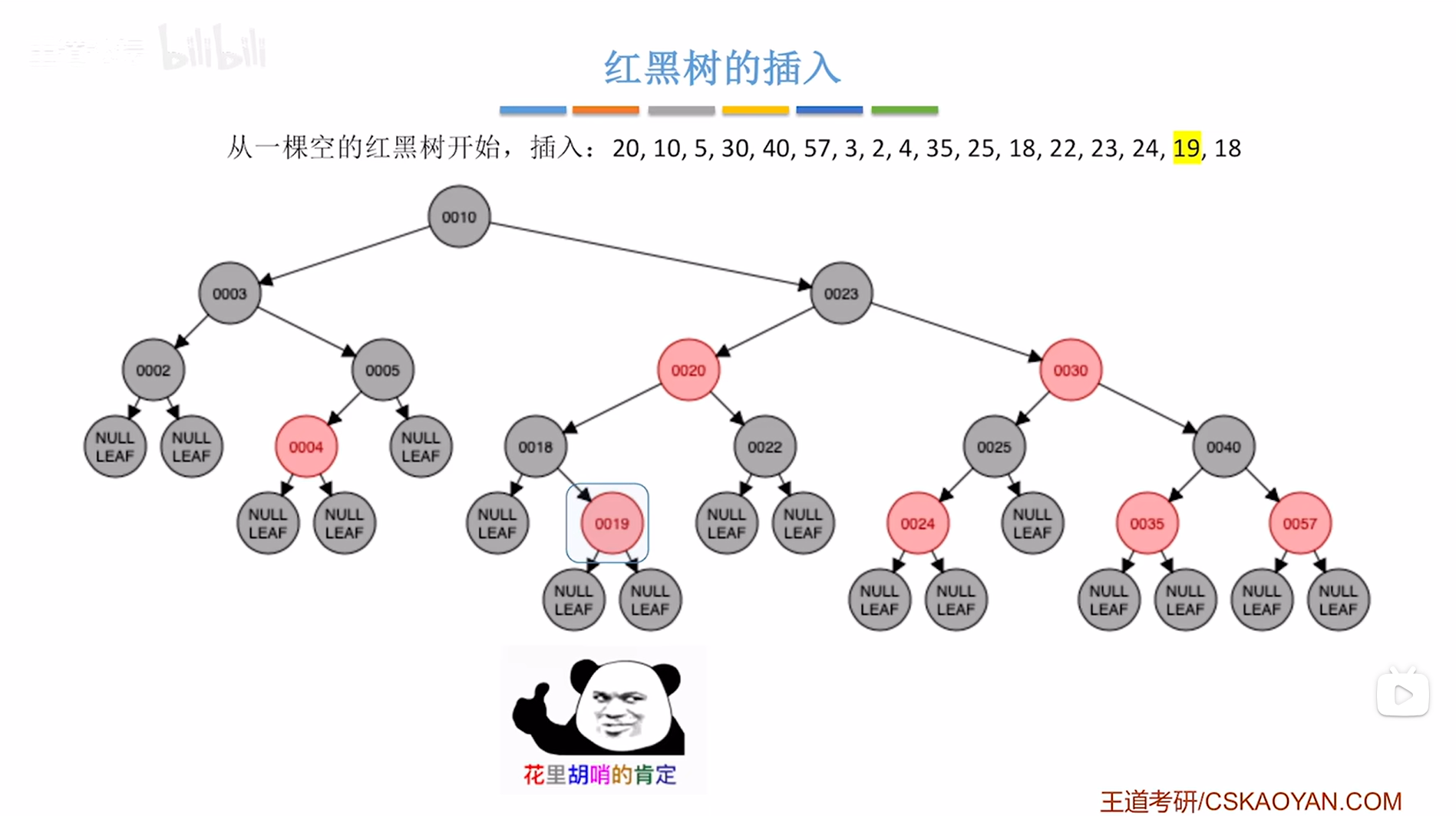
如上图，

新插入的结点是结点19，结点19是非根结点，所以只需要判断是否破坏"不红红"，显然没有破坏，

此时满足红黑树的定义。

接下来要插入结点18，但在之前已经插入结点18了，那这个结点18应该插入到哪里呢？

注：数据结构是应用科学，而不是理论科学，所以它没有所谓的标准答案，

当出现了两个相同的结点时，根据当前的应用场景自行规定插入的位置，可以不插入，可以优先插在左子树，也可以优先插在右子树，

现在假设优先插在右子树，根据二叉排序树的插入规则可知结点18要插在结点19的左子树上，并把结点18涂红，

如下图：

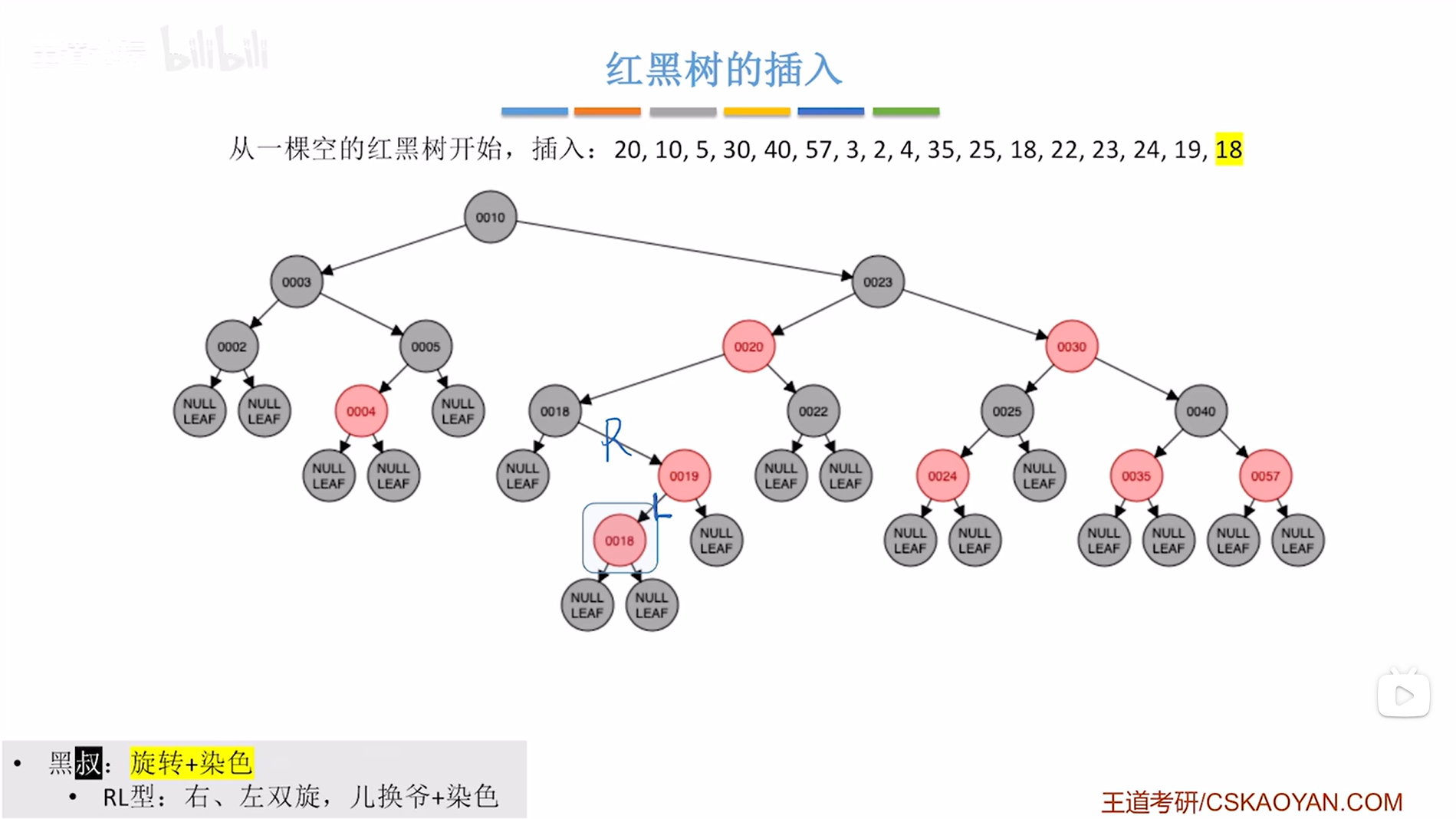
如上图，

此时红色的结点18违反了红黑树"不红红"的特性即红黑树中不可以出现连续的两个红结点（详情见"7.8.红黑树的定义和性质(红黑树英文缩写为RBT)"），因此就需要进行调整->

调整策略核心就是要看红色的结点18的叔叔结点的颜色，

红色的结点18的父结点是19结点，19结点的兄弟结点是NULL LEAF结点(黑色的结点18的左孩子)，

所以红色的结点18的叔叔结点是NULL LEAF结点(黑色的结点18的左孩子)，NULL LEAF结点(黑色的结点18的左孩子)是黑色结点，

因此需要"旋转+染色"->

由于结点19的父结点是黑色的结点18，所以红色的结点18的爷爷结点是黑色的结点18，

因此红色的结点18属于RL型即"新插入的红色的结点18位于它的爷爷黑色的结点18的右孩子的左子树上"

对于RL型的处理方法要先右旋，再左旋使得儿换爷，最后进行染色->关键是把儿结点换到爷结点的位置，新插入的结点就是儿子结点，先通过右旋换到父结点的位置，再通过左旋换到爷结点的位置；染色的操作是如果原来的结点是红色，染色后变为黑色；如果原来的结点是黑色，染色后变为红色，

其中红色的结点18的父结点是19，爷结点是黑色的结点18，

通过右旋让红色的结点18换到父结点19的位置，由于父结点19大于结点18，所以以父结点19为根结点的树要挂在结点18的右子树上（要保证二叉排序树的特性"左<根<右"），

如下图：

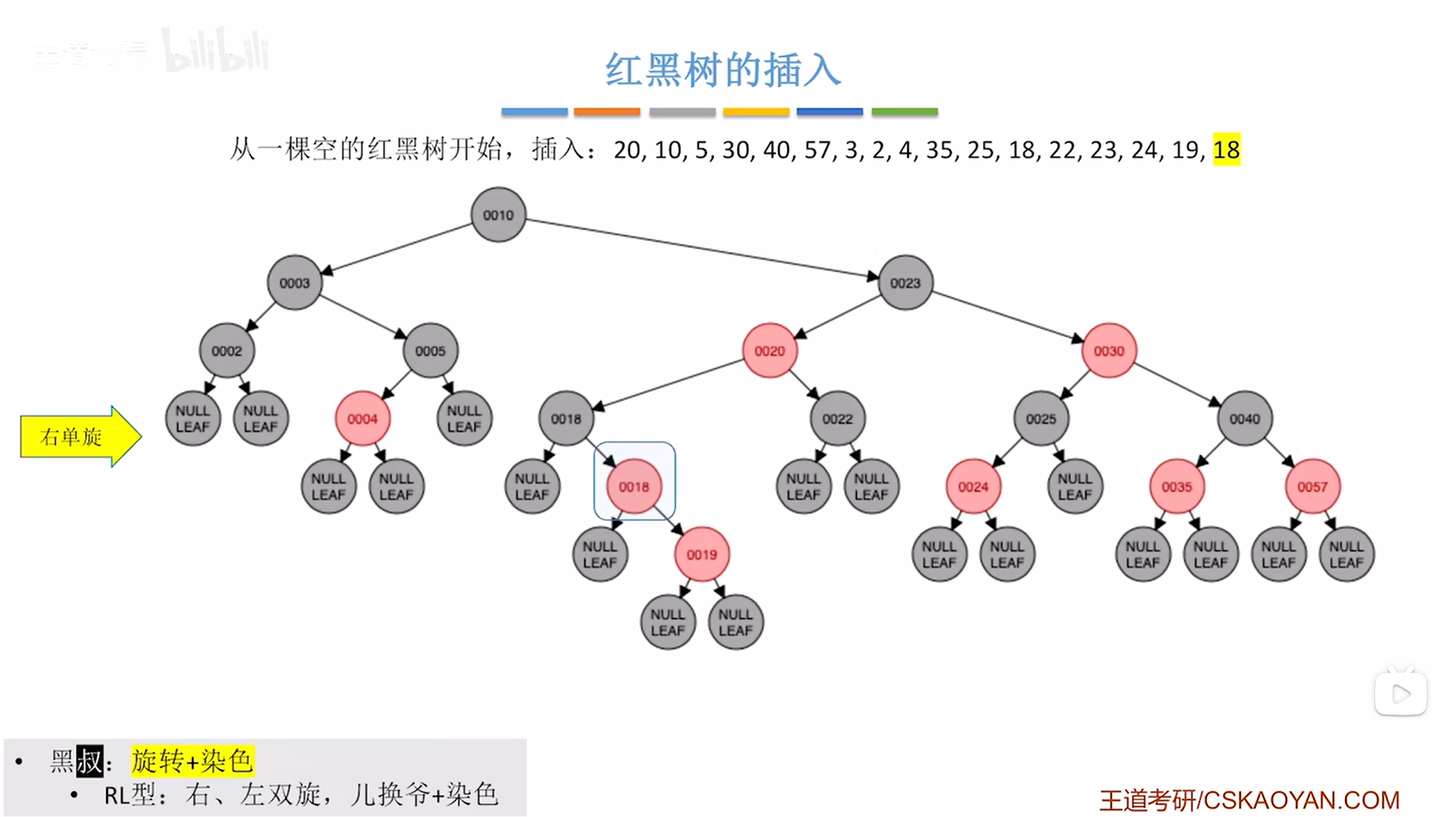
如上图，

再通过左旋把红色的结点18换到爷爷黑色的结点18的位置，

如下图：

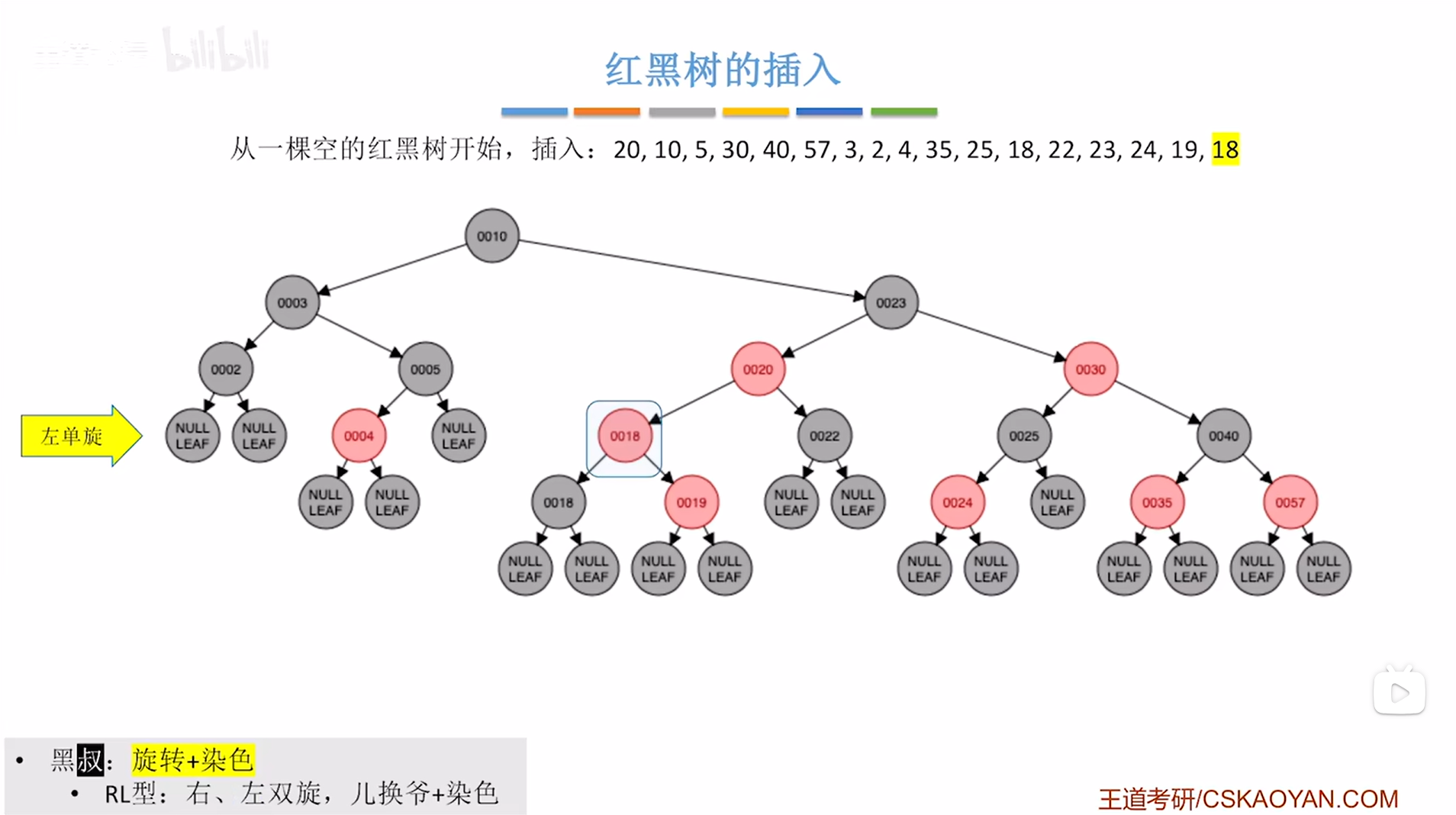
如上图，

旋转之后还需要染色，对于染色，处理的是儿子结点即红色的结点18和爷结点即黑色的结点18，

儿子结点即红色的结点18原本是红色，染色后为黑色，爷结点即黑色的结点18原本是黑色，染色后为红色，

如下图：

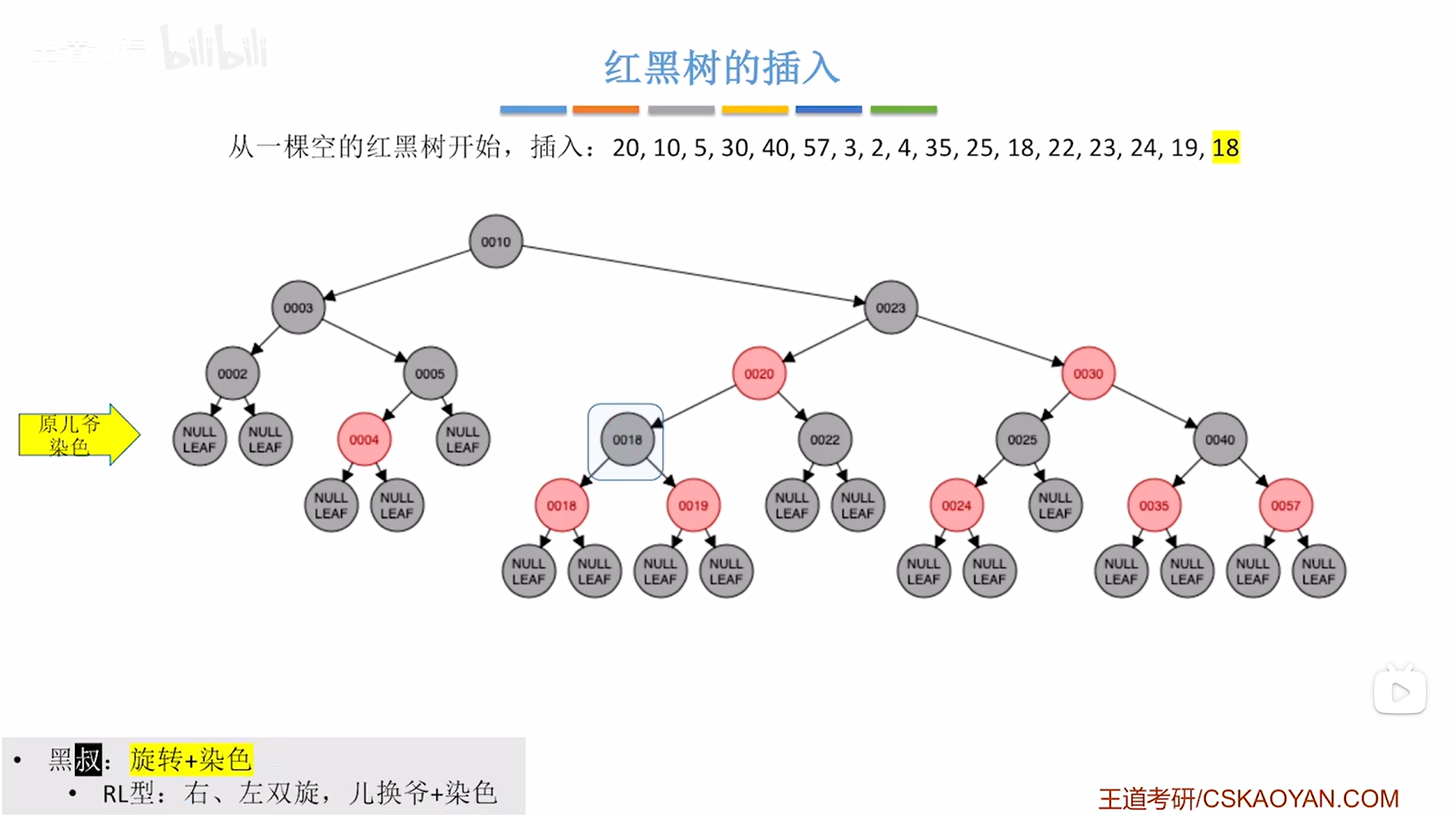
如上图，

此时满足红黑树的定义。

至此，完成了所有结点的插入，红黑树的插入算法结束。

---

二.总结：

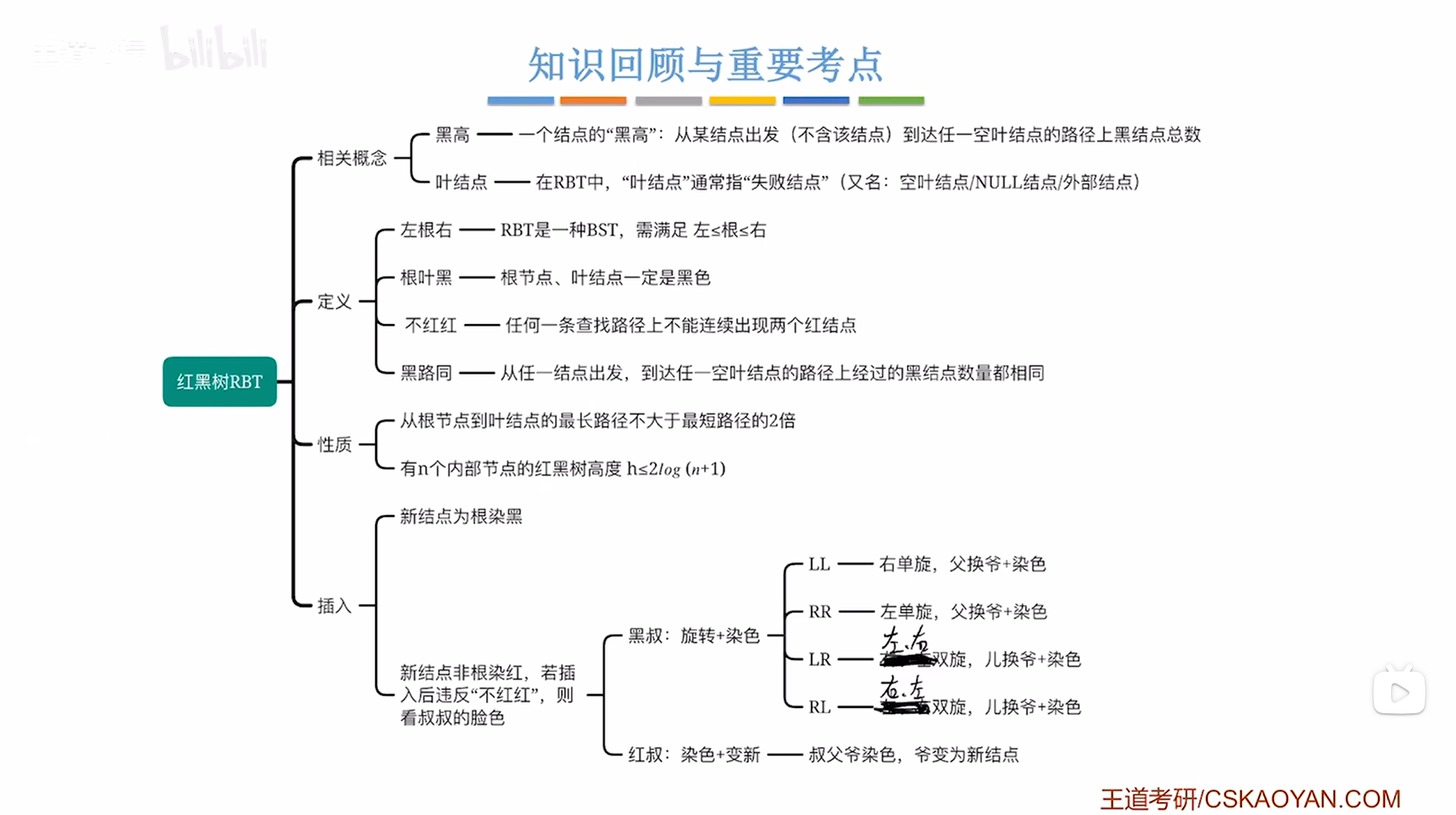
• 红黑树(RBT)是一种特殊的二叉排序树(BST)，因此红黑树(BST)需满足"左≤根≤右"

---

三.红黑树练习方法(插入操作)：

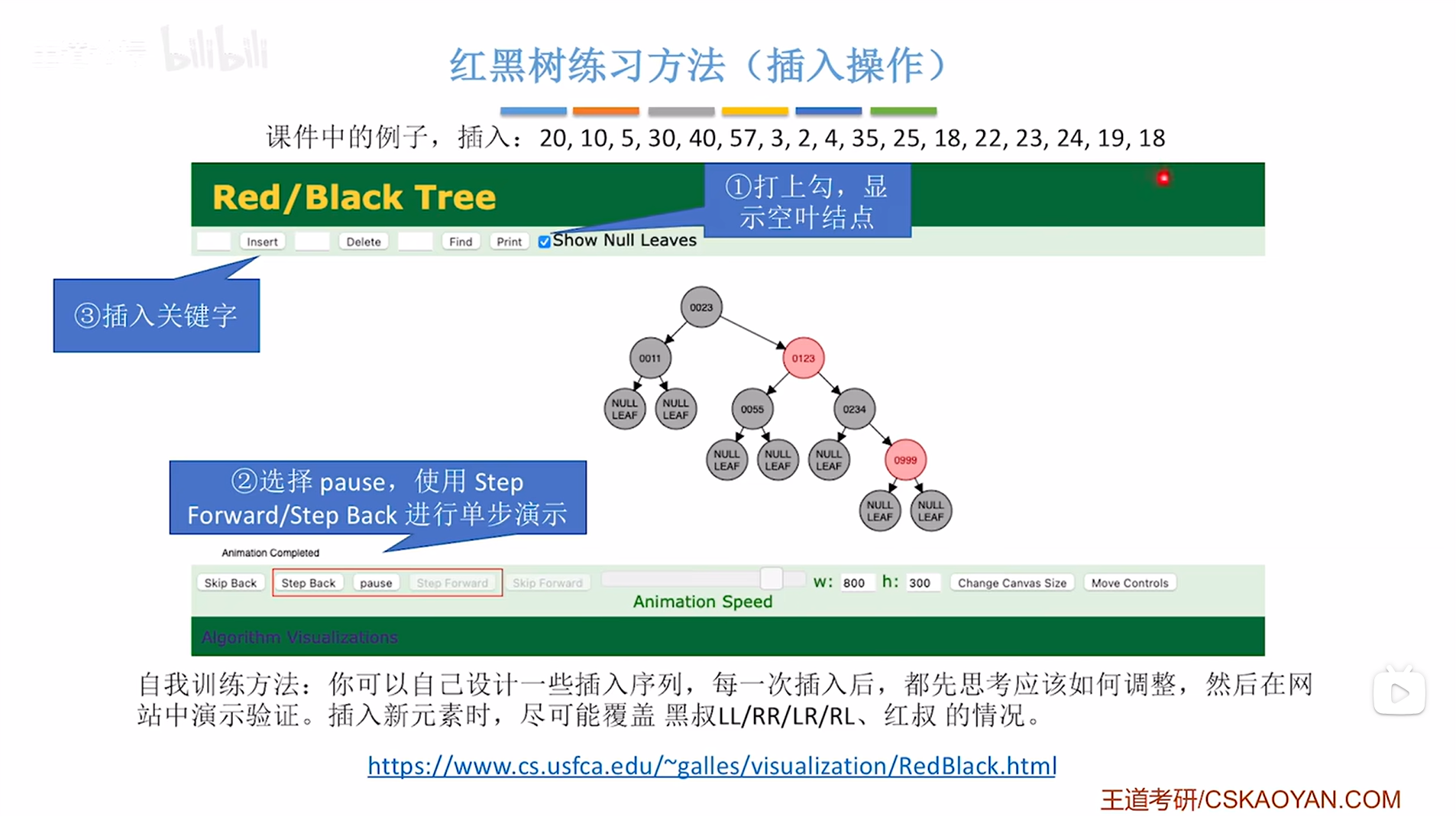
上述图片下方的网站可以找到模拟红黑树插入的内容。

---