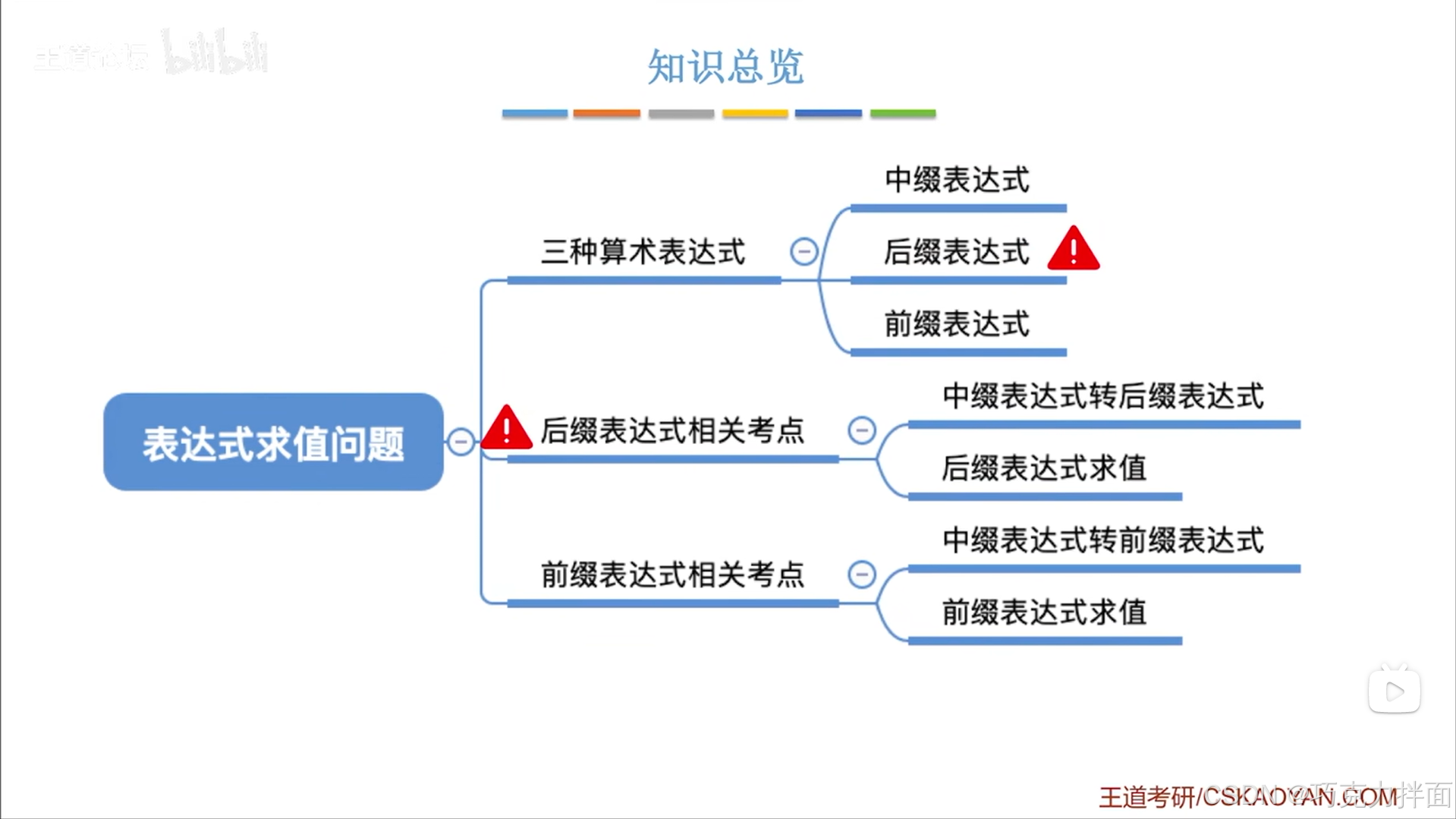
一.算术表达式:

-
操作数:被操作的数或字符等;运算符:+,-,*,/,%等;界限符:()之类的
-
界限符表明了各个运算符生效的顺序,如果没有界限符就会导致运算混乱
二.中缀、后缀、前缀表达式:
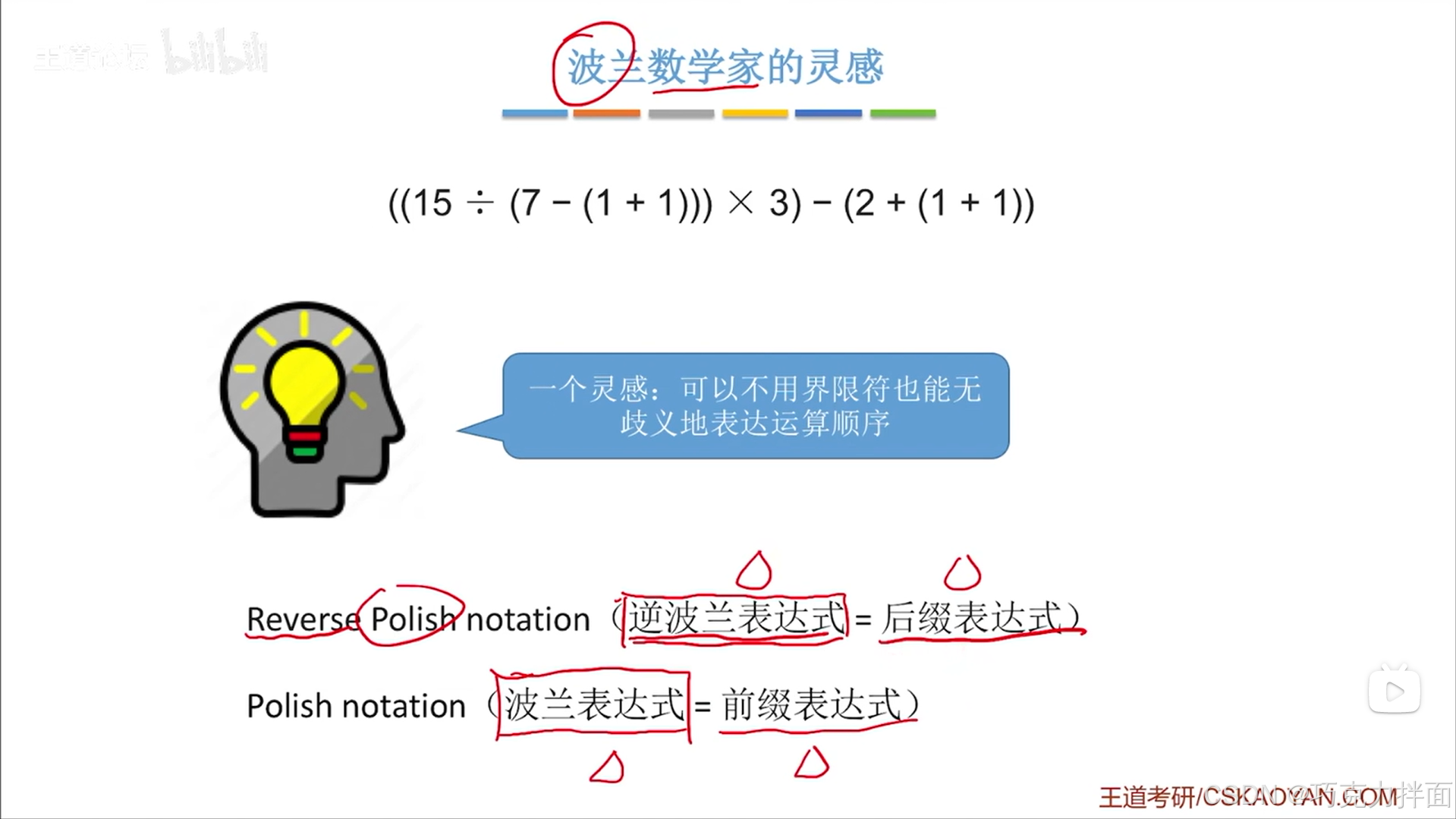
1.注:例如后缀表达式:ab/和ba/是不一样的,ab/相当于a/b,ba/相当于b/a
2.中缀表达式转换为后缀表达式:
-
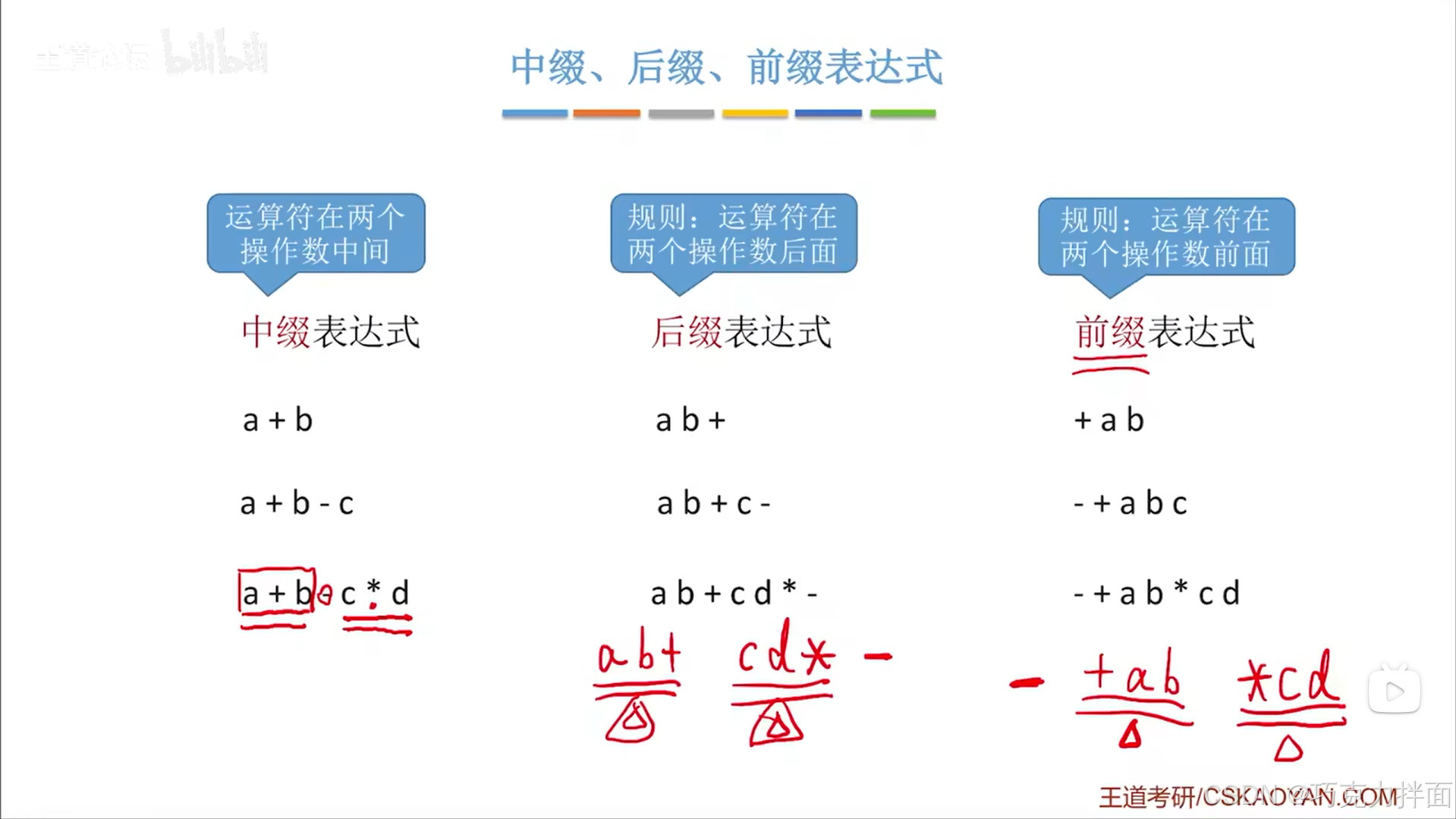
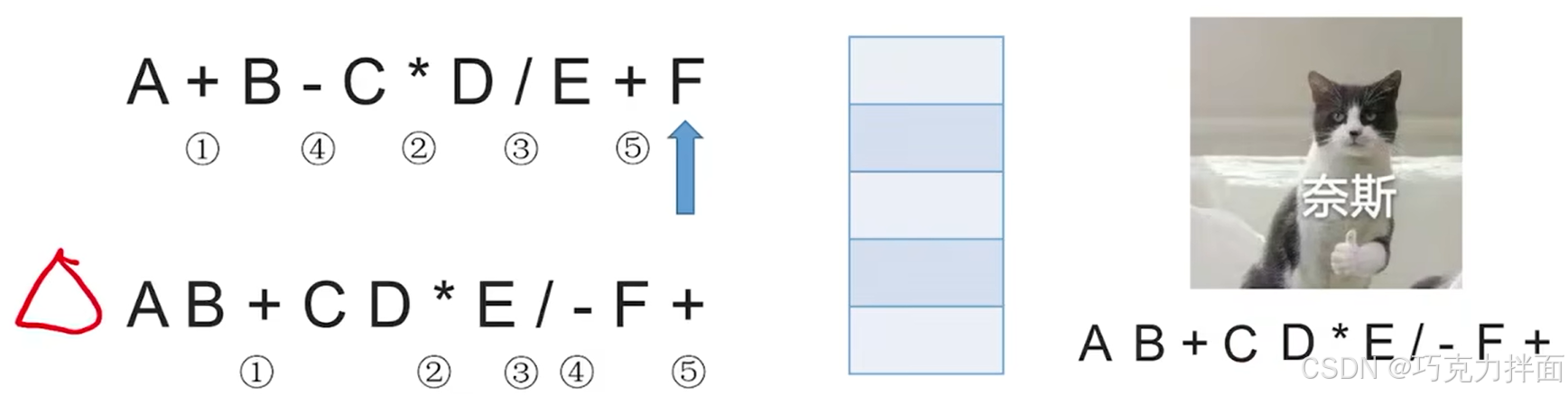
例一:a+b-c可以先算a+b即ab+,再算-c即ab+ c -(类似的,也可以先算b-c即bc-,再算a+即a bc- +)
-
例二:a+b-c*d可以先算a+b即ab+,根据运算规则,需要算c * d即cd*,最终做差即ab+ cd * -
3.中缀表达式转换为前缀表达式:
-
例一:a+b-c可以先算a+b即+ab,再算-c即- +ab c
-
例二:a+b-c*d可以先算a+b即+ab,根据运算规则,需要算c * d即*cd,最终做差即- +ab *cd
三.中缀表达式与后缀表达式、前缀表达式的相互转化:
核心:
-
中缀转后缀:"左优先"
-
中缀转前缀:"右优先"
1.中缀表达式转后缀表达式:

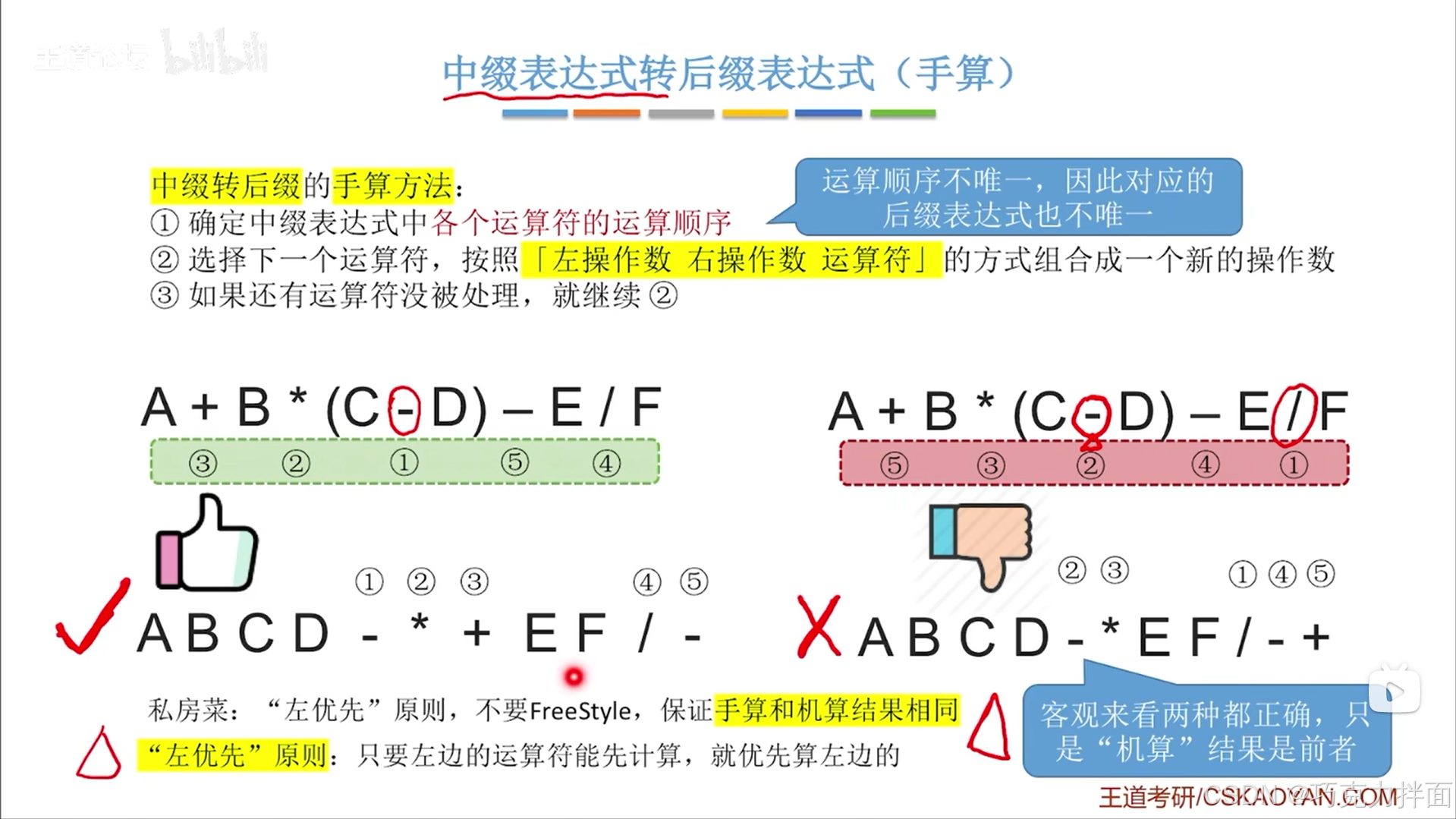
计算机操作时后缀表达式中运算符出现的先后顺序和中缀表达式中运算符生效的顺序一致,但人为操作时可能不一致
-
考试时后缀表达式的结果要用上图中左边的后缀表达式的结果(打红对勾的),和计算机统一
-
"左优先"原则:就比如上图的例子,既然绿框里靠左的减法可以比红框里靠右的除法先生效,那么就按绿框里靠左的减法来
-
FreeStyle译为自由
-
实例:

2.后缀表达式转中缀表达式:
-
关键:按照"左优先"原则的话后缀表达式中运算符出现的先后顺序和中缀表达式中运算符生效的顺序一致
-
方法:先找第一个运算符和该运算符对应的前两个数字,此时就消耗了一个运算符和两个运算数,把这两个运算数的结果和前一个数字和第二个运算符进行操作,以此类推,直至算完
例一:

例二:

3.中缀表达式转前缀表达式:

例如中缀表达式A + B * (C - D) - E / F,根据运算规则先算C - D,转为前缀表达式为-CD,然后算B *,即 *B -CD,
再算A +,即+A *B -CD,之后算E/F即/EF,最后算-即- +A *B -CD /EF。

-
如果按照"左优先"原则的话由中缀表达式转化成前缀表达式后两者的运算顺序没太大关系,
-
如果按照"右优先"原则的话由中缀表达式转化成前缀表达式后前缀表达式的运算顺序刚好是从右到左依次生效的
四.利用栈实现后缀表达式的计算:
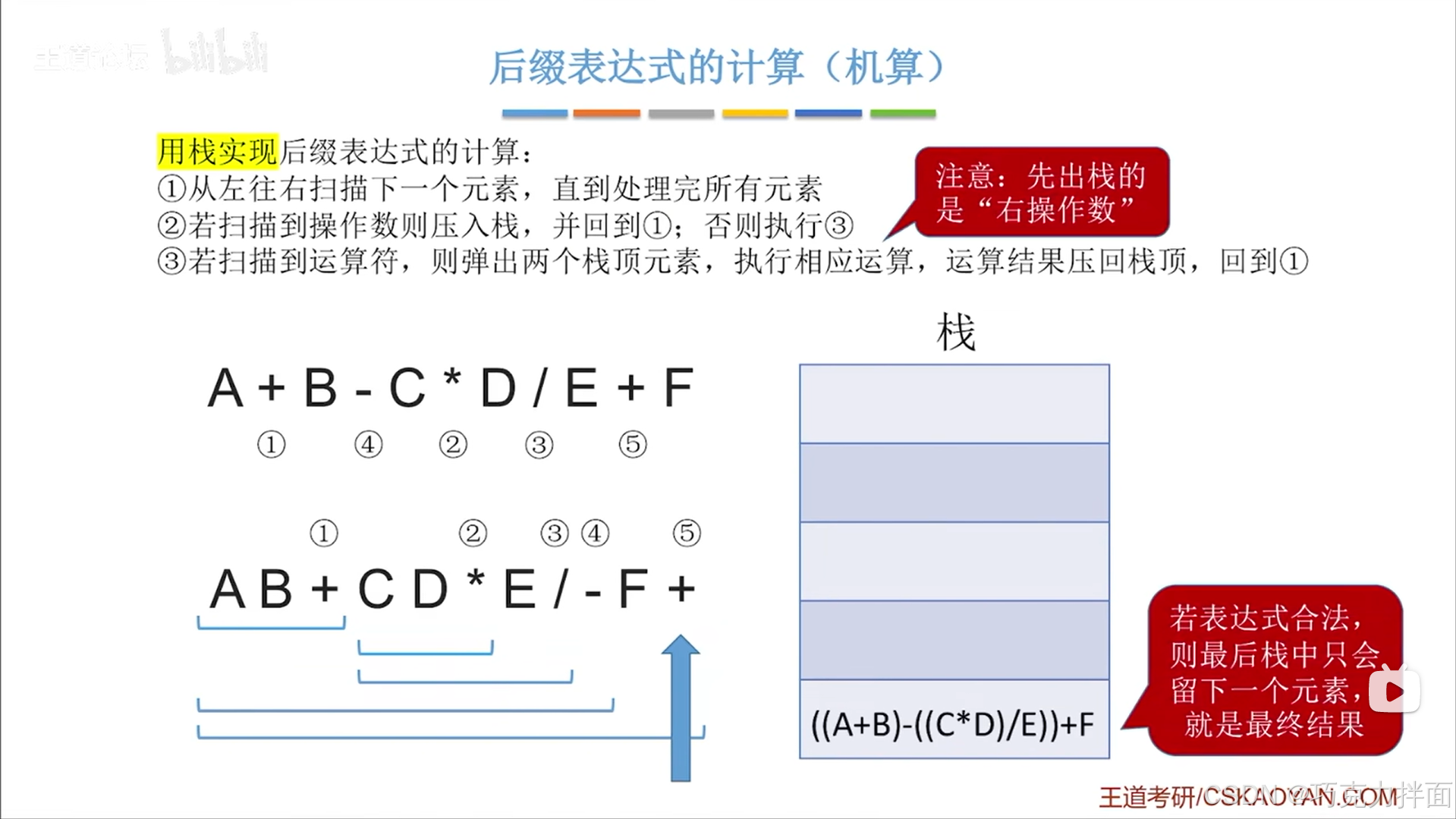
1.思考:最后出现的操作数先被运算,比如操作两个数,已经进去了一个数,一旦第二个数进入就会被运算即后进先出,也就是栈
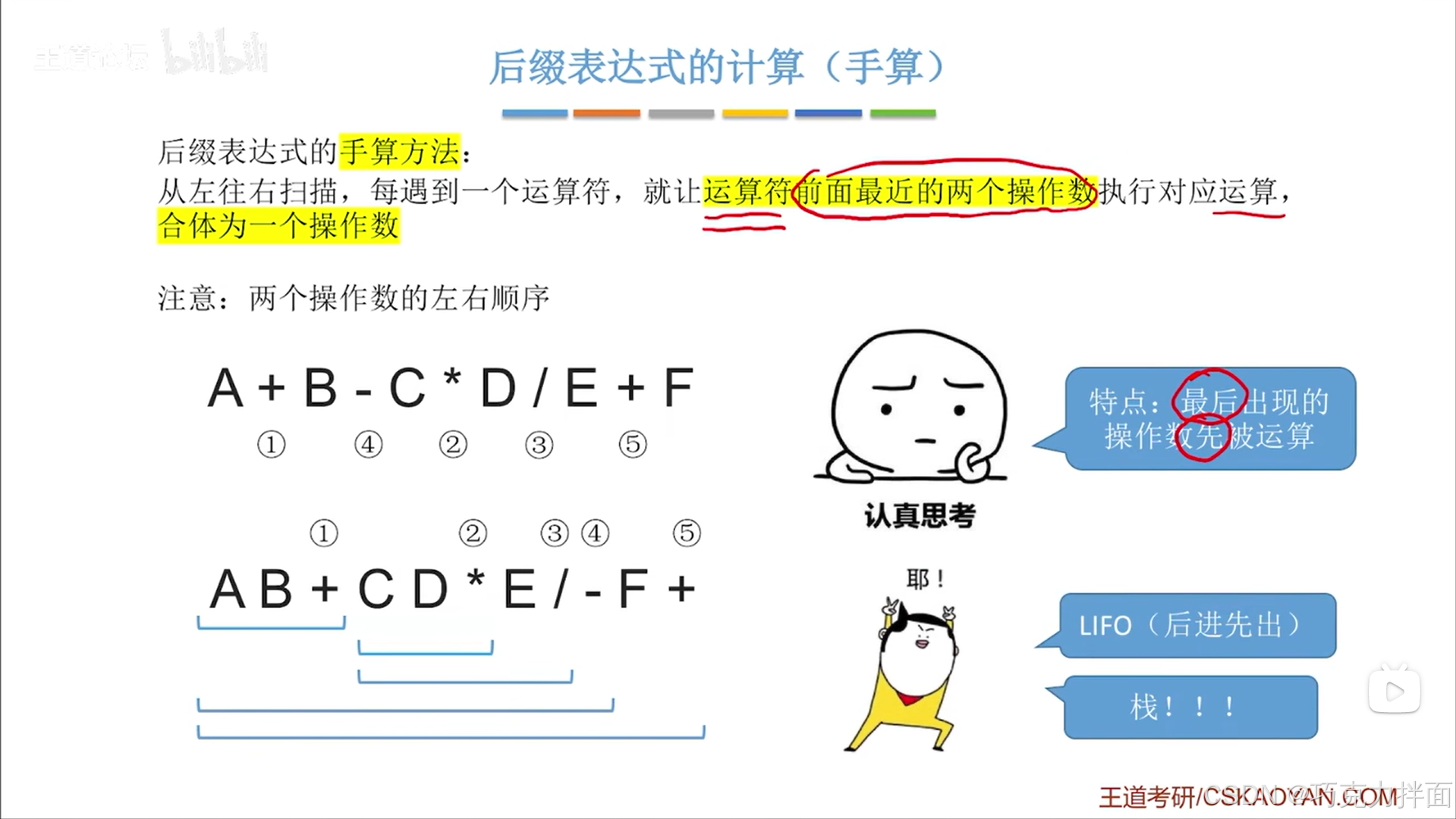
2.操作原理:核心是从左往右扫描,为了保证转换的唯一性即确定性(注:后缀表达式中先出栈的操作数做被操作的数即右操作数)
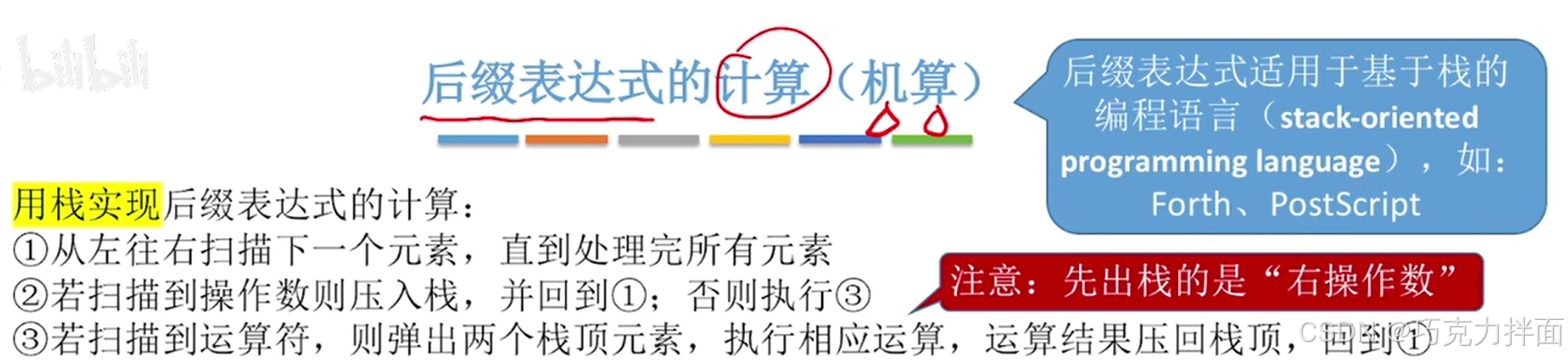
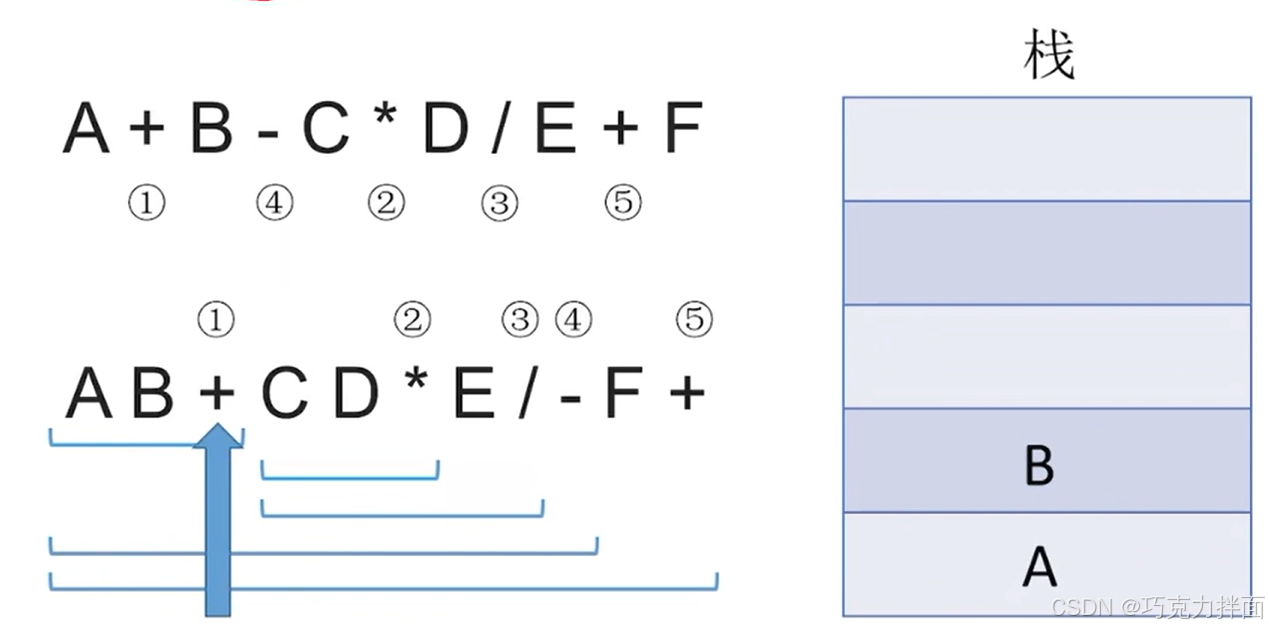
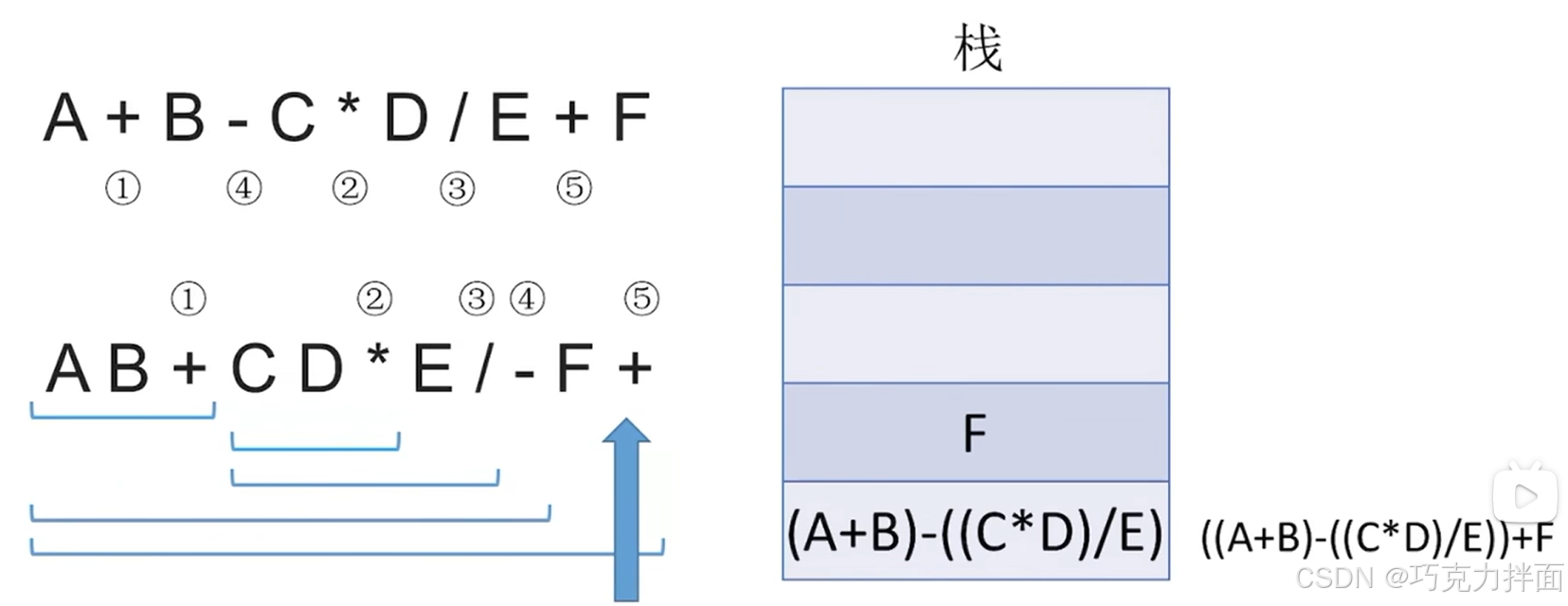
例如后缀表达式A B + C D * E / - F +,开始依次往后扫描,首先第一个数据为操作数A,因此进栈:
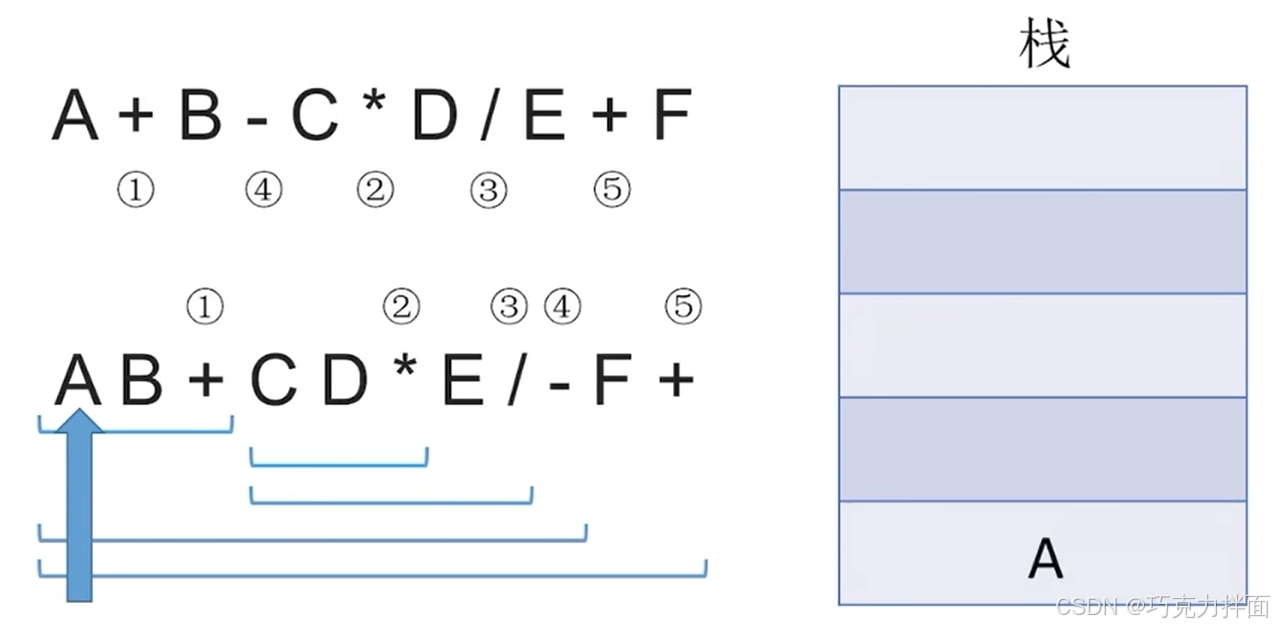
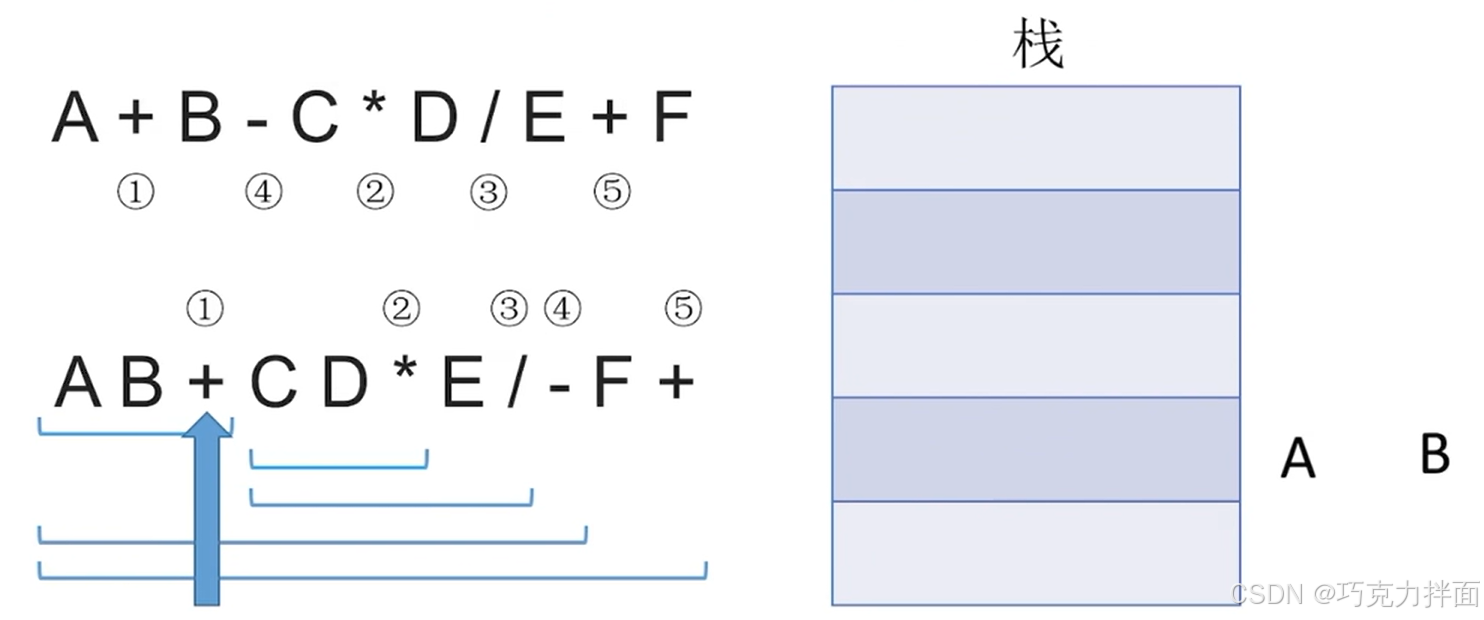
继续往后扫描,第二个数据为操作数B,因此进栈:
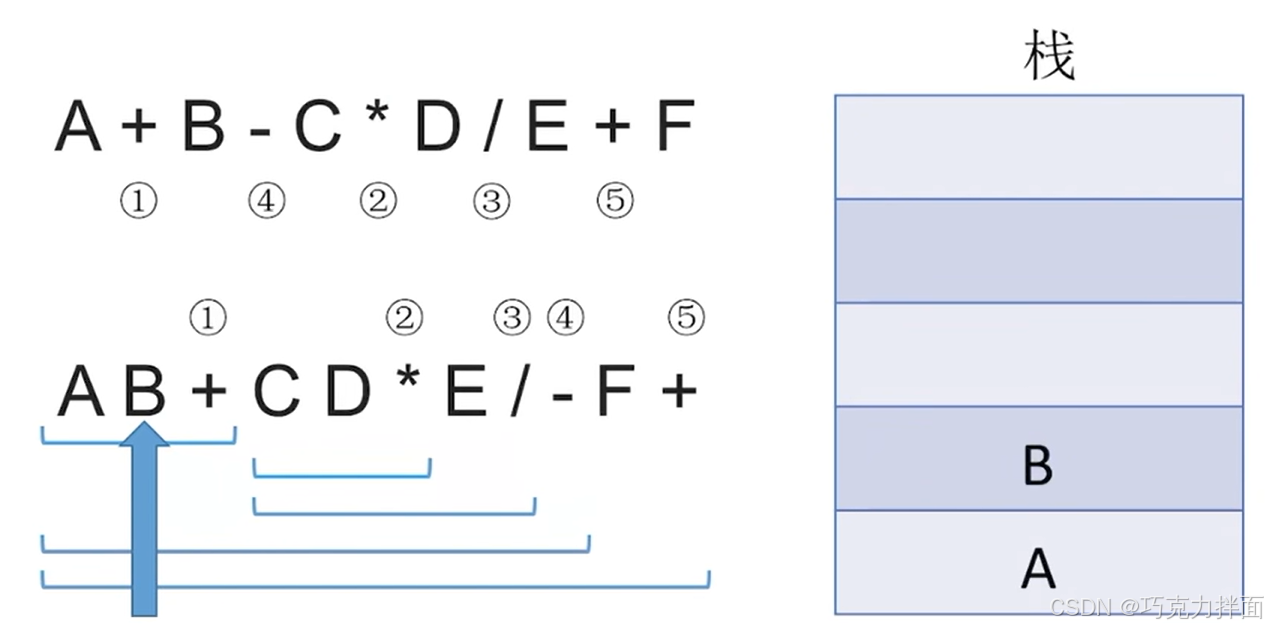
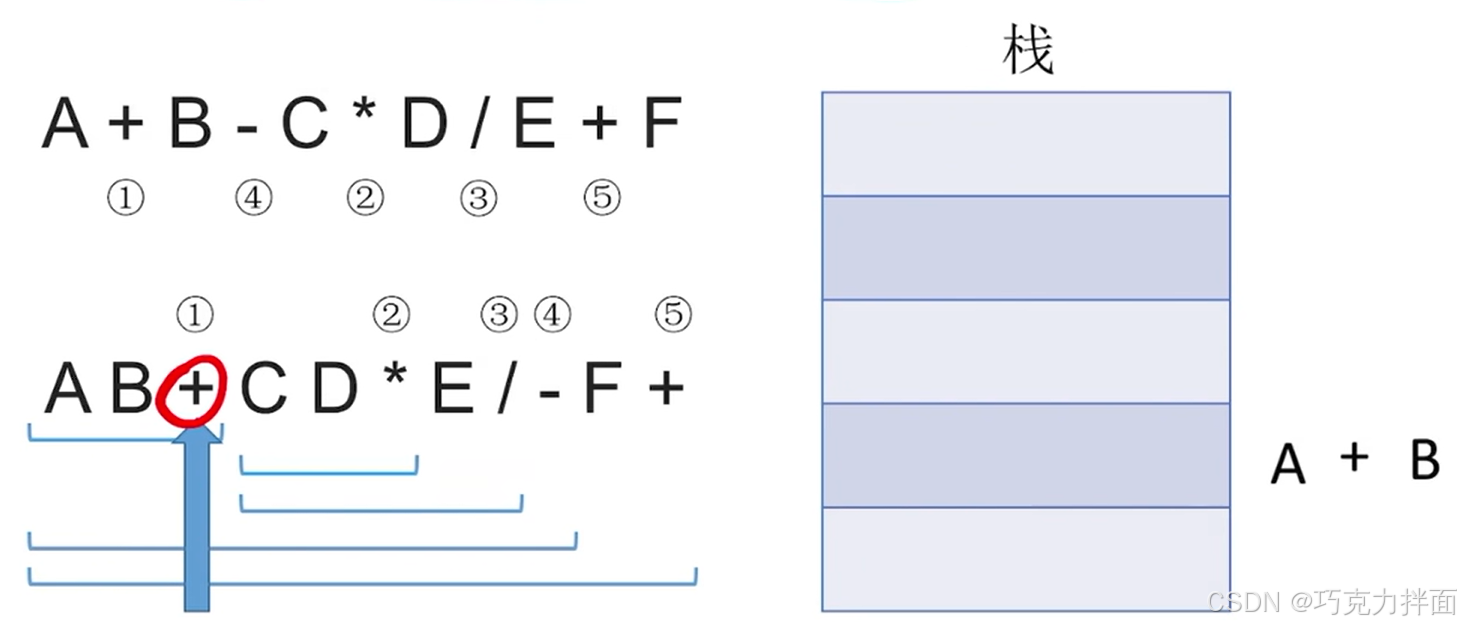
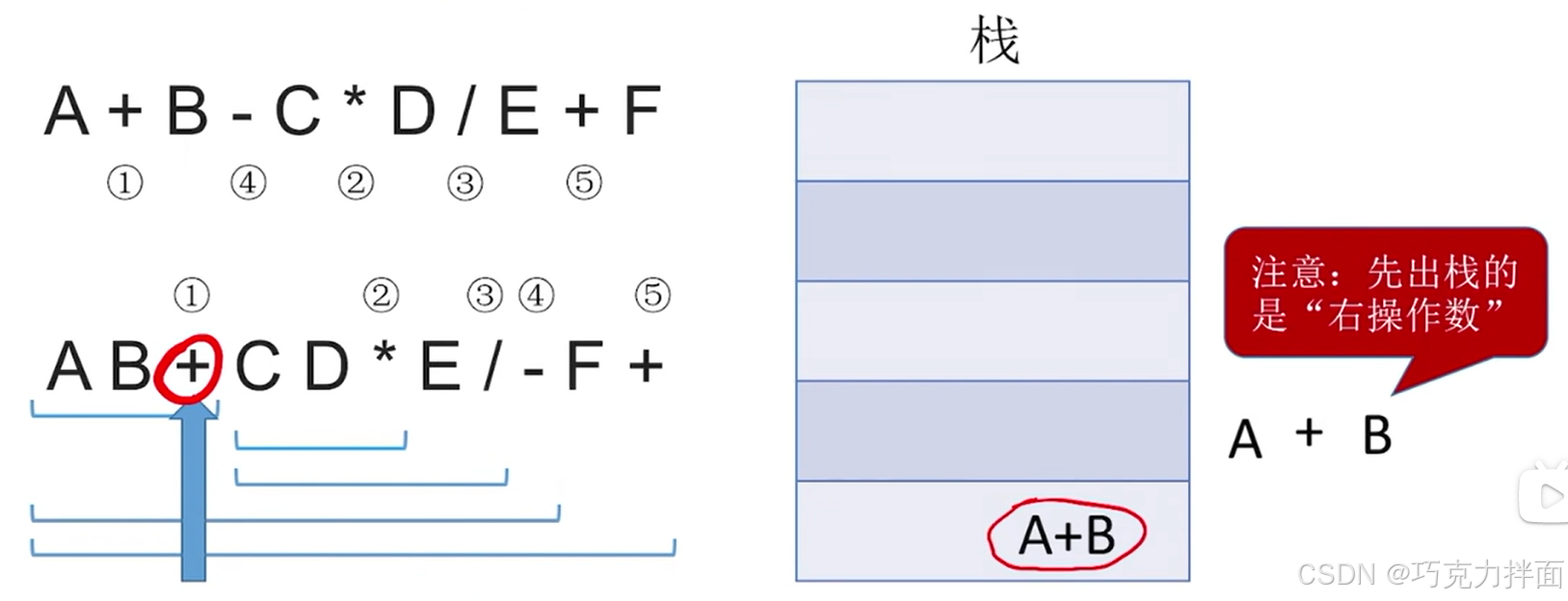
继续往后扫描,第三个数据为运算符+,所以要弹出两个栈顶元素即A和B,进行+运算,结果为A+B,运算结果A+B压回栈顶:A和B中B比A先出栈,因为B是右操作数
继续往后扫描,第四个数据为操作数C,第五个数据为操作数D,进入栈顶:
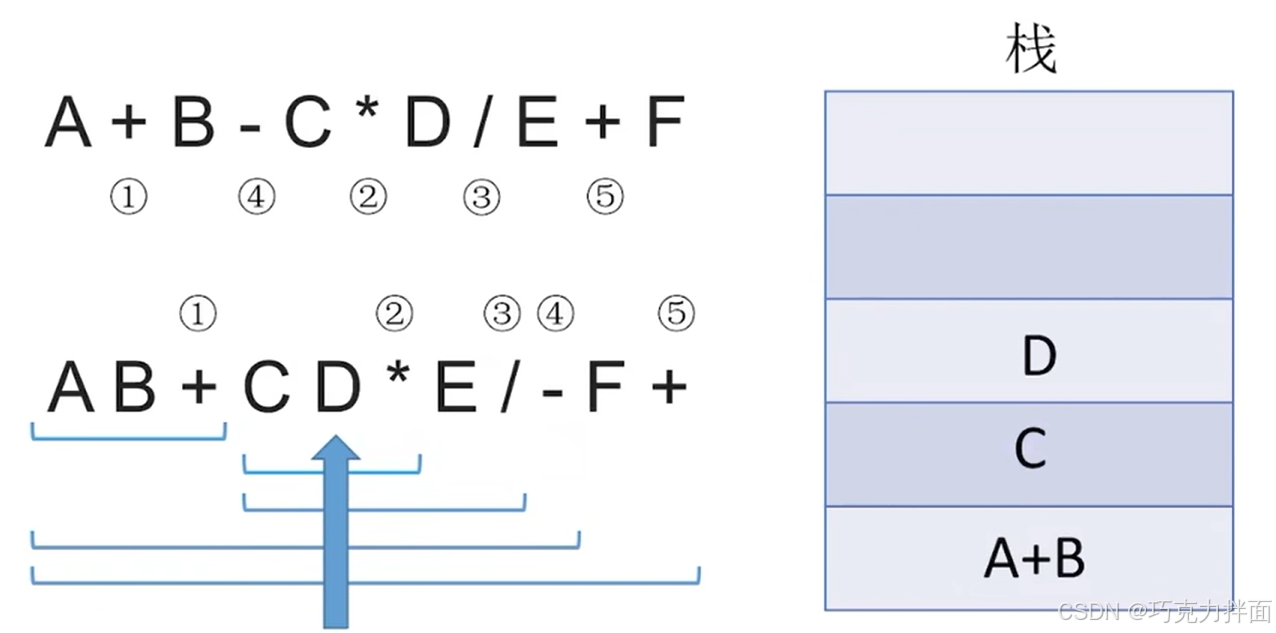
继续往后扫描,第六个数据为运算符*,此时栈顶的两个元素即C和D出栈,进行 *运算,结果为C * D,该结果再压入栈顶:
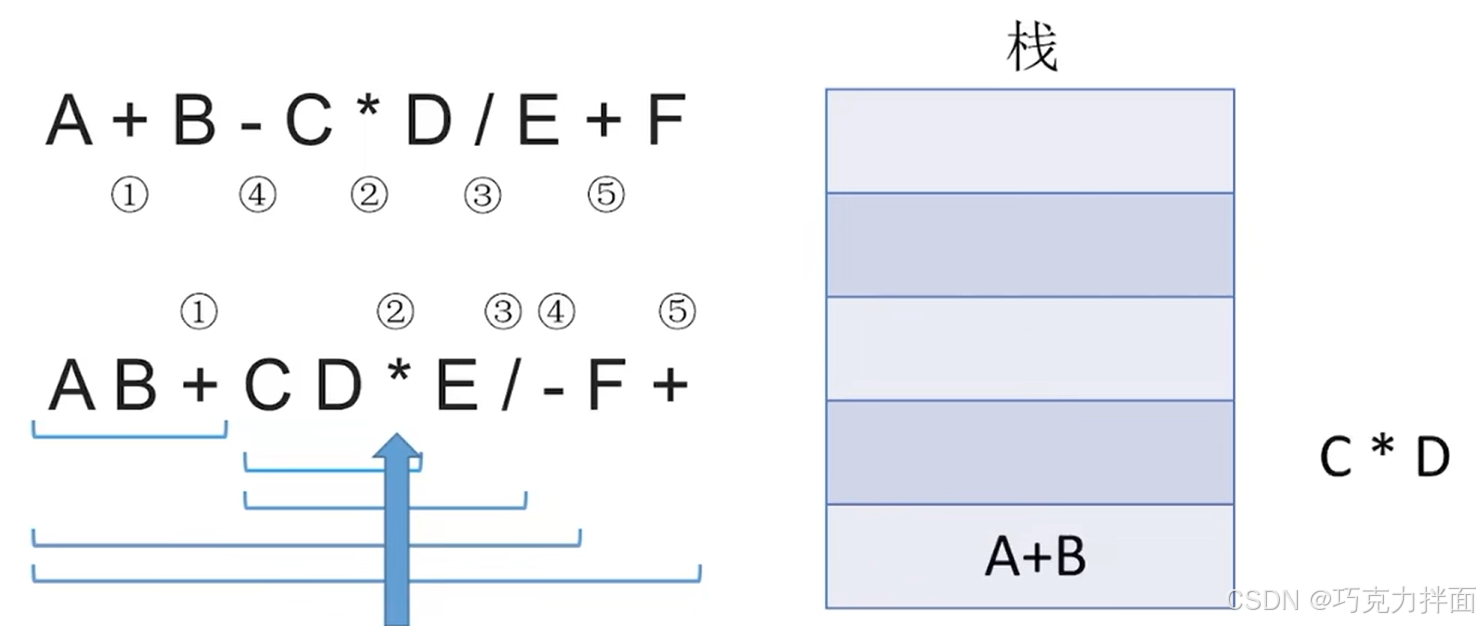
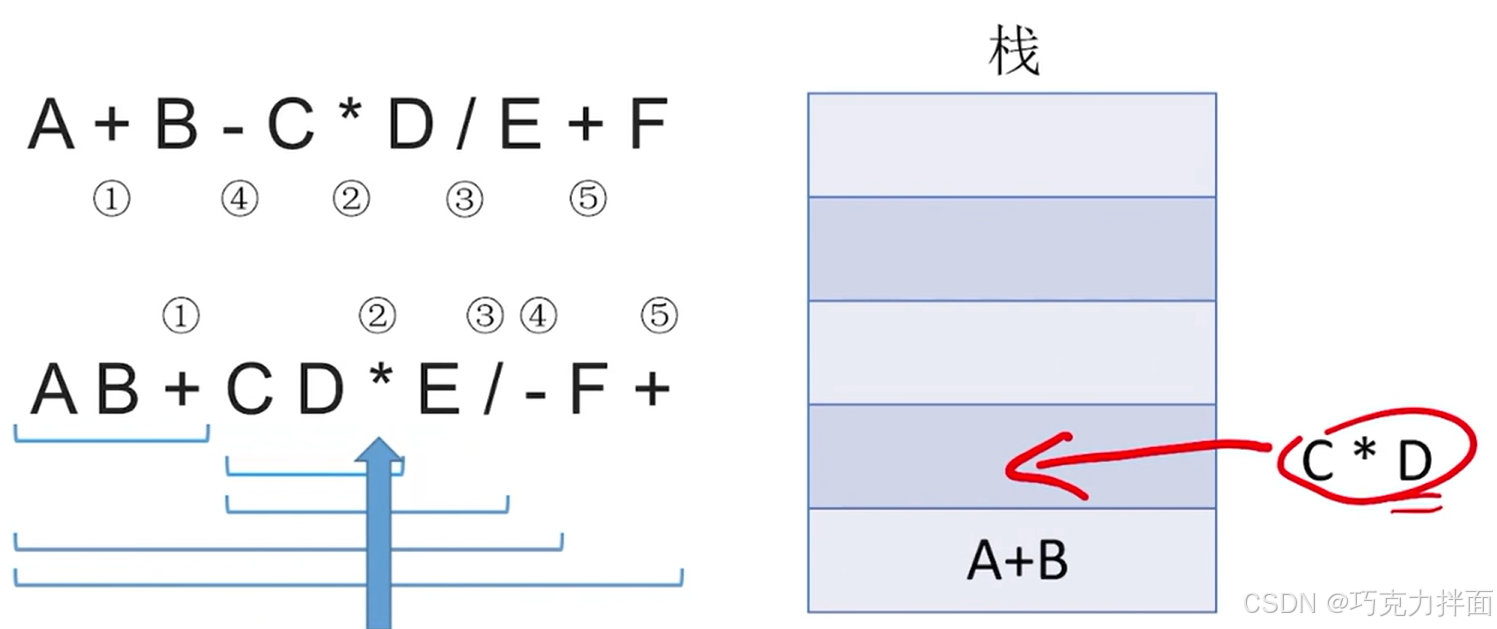
继续往后扫描,第七个数据为操作数E,因此E压入栈顶:
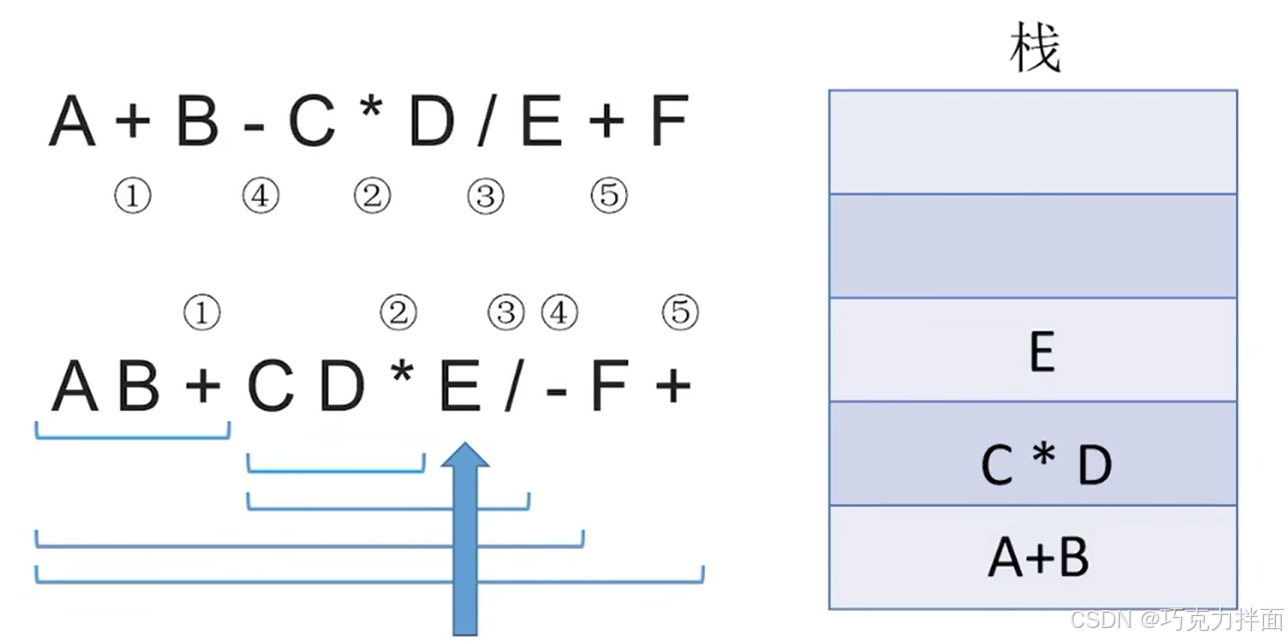
继续往后扫描,第八个数据为运算符/,此时需要弹出两个栈顶元素即E和C*D(注:E是右操作数,先出栈),进行/运算,结果为(C * D)/E,该结果再压入栈顶:
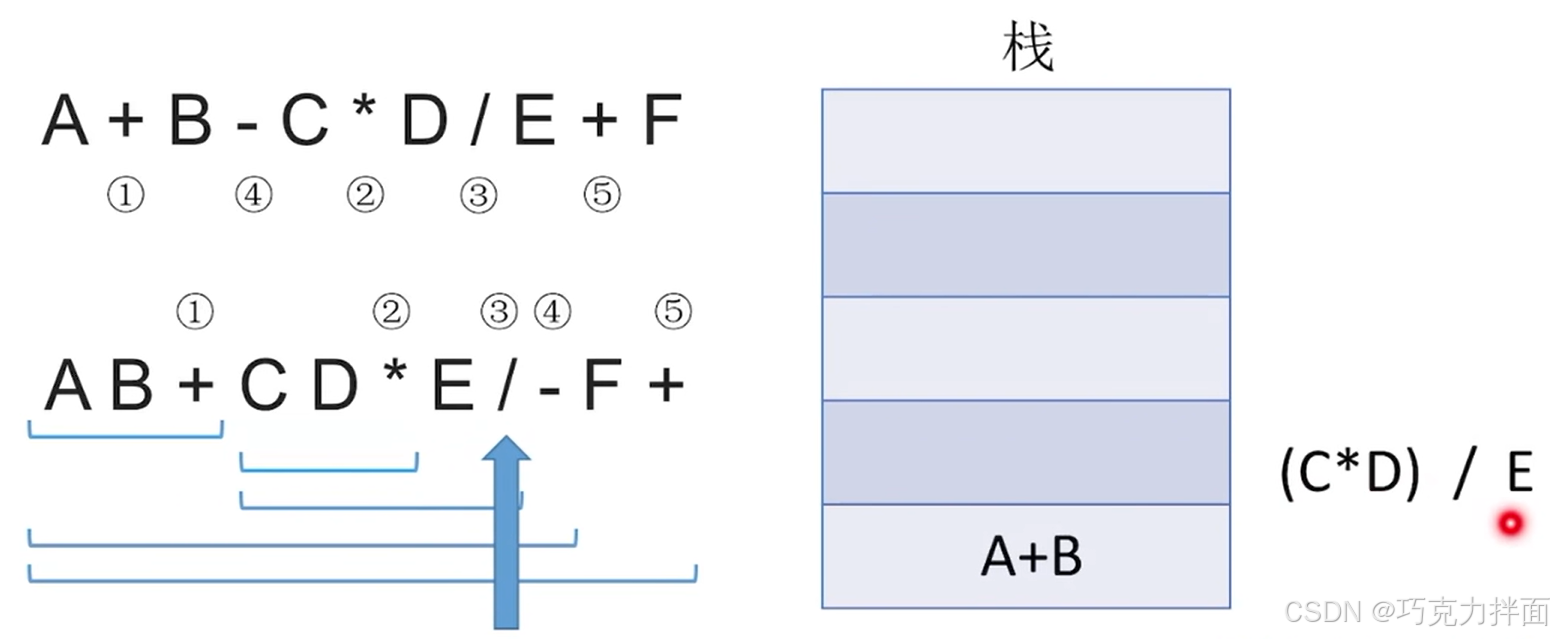
继续往后扫描,第九个数据为运算符-,此时需要弹出两个栈顶元素即(C * D)/E和A+B,进行-运算,结果为(A+B)-( (C * D)/E ),该结果再压入栈顶:
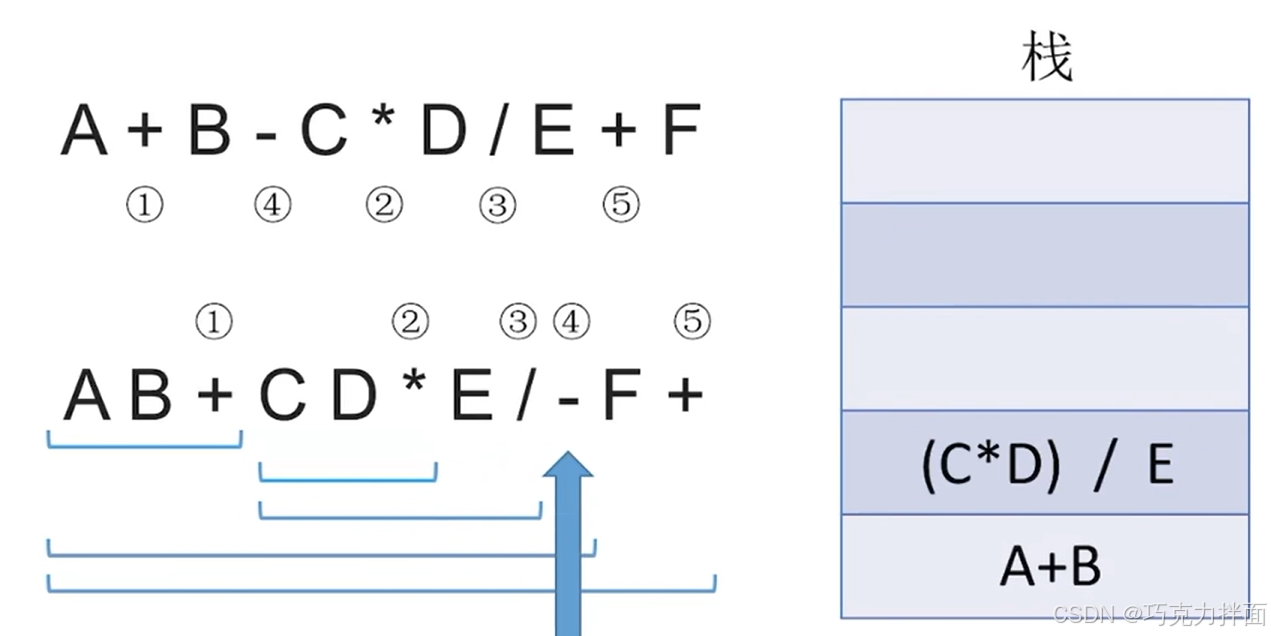
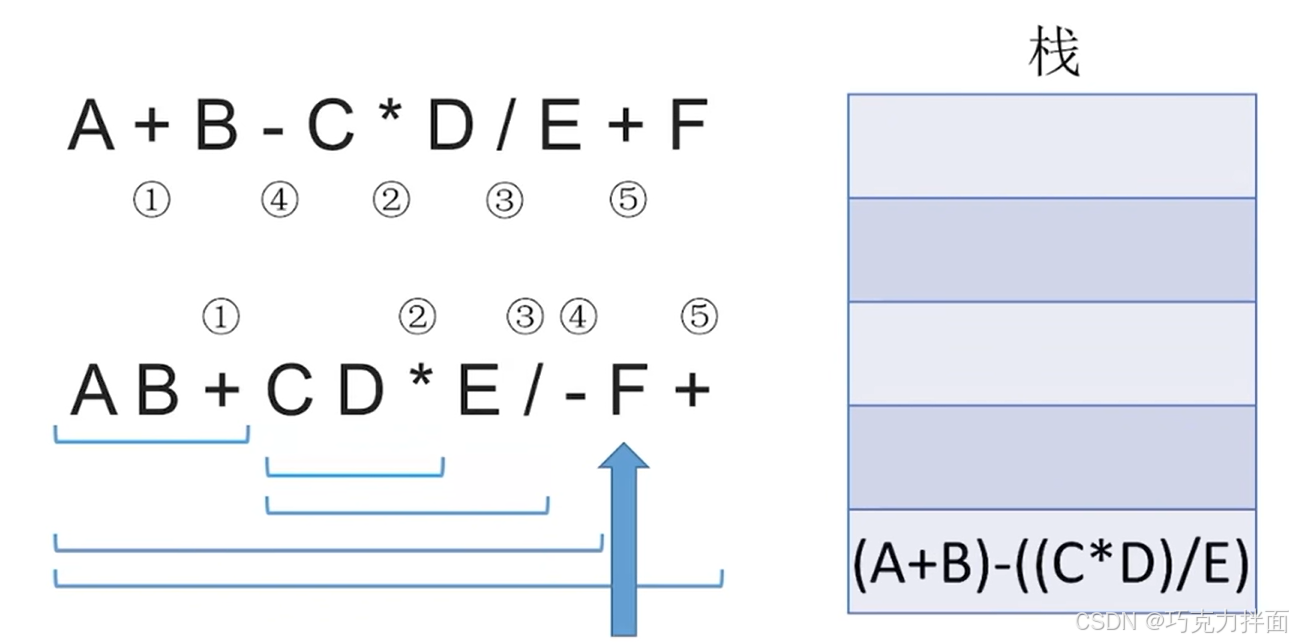
继续往后扫描,第十个数据为操作数F,因此压入栈顶:
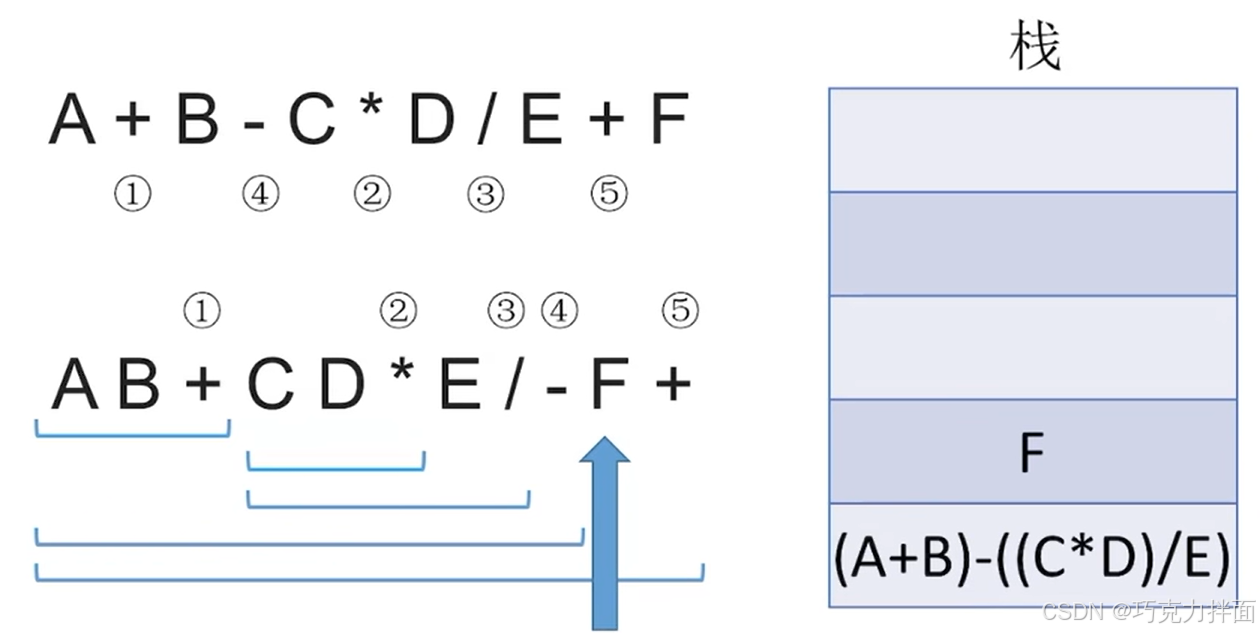
继续往后扫描,第十一个数据为运算符+,此时需要弹出两个栈顶元素即F和(A+B)-( (C * D)/E ),进行+运算,结果为
(A+B)-( (C * D)/E )+F,该结果压入栈顶:
-
上述过程也刚好实现了后缀表达式转中缀表达式
-
对于计算机而言后缀表达式要比中缀表达式计算起来更方便,因为后缀表达式无需再判断运算符计算的先后顺序,只需要按照从左向右依次计算即可,而如果是中缀表达式的话就需要判断哪些运算符先生效
五.利用栈实现前缀表达式的计算:
操作原理:核心是从右往左扫描,为了保证转换的唯一性即确定性(注:前缀表达式中先出栈的操作数做操作的数即左操作数)

实例:

六.表达式求值问题总结:
一个中缀表达式可以对应多个后缀、前缀表达式,因为如a+b-c,可以先算+,也可以先算-
七.用栈实现中缀表达式转后缀表达式(机算):
中缀表达式转后缀表达式后,两个表达式中的操作数的相对顺序不变,但运算符的相对顺序会改变

1.规则解读:
-
第三条规则中运算符优先级:乘和除 > 加和减(注:乘和除优先级一样,加和减优先级一样)
-
是从左向右扫描
2.实例:
例一:
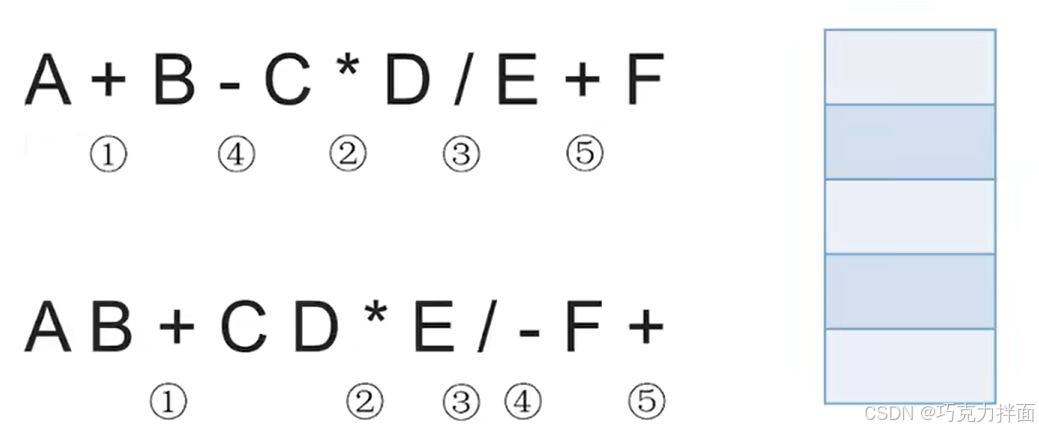
从左往右开始扫描中缀表达式,第一个数据为操作数A,因此直接输出,放入后缀表达式中:
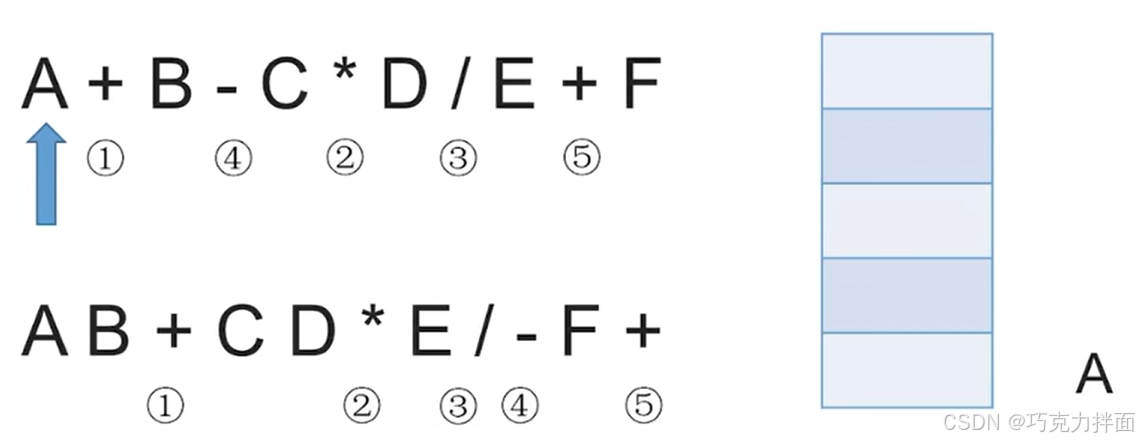
第二个数据为运算符+,此时栈空,因此入栈:
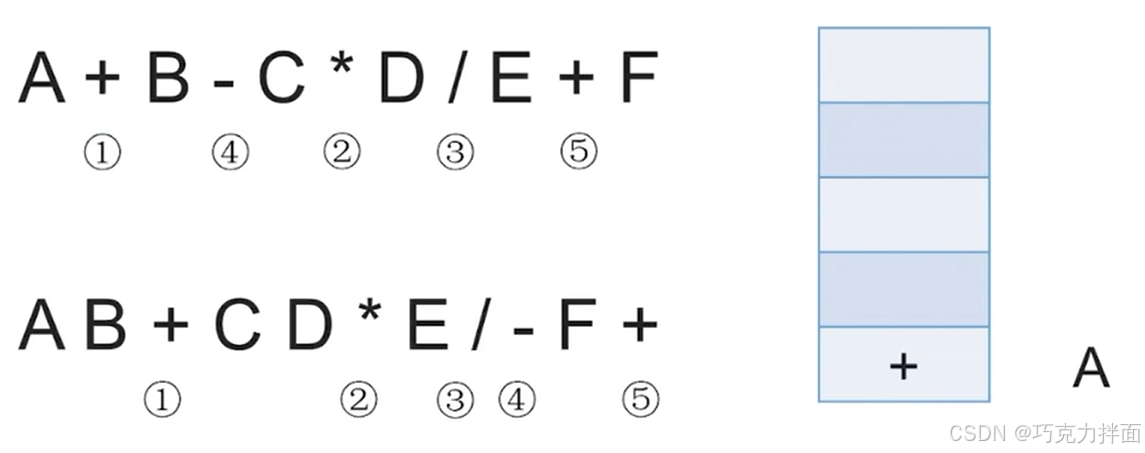
第三个数据为操作数B,因此直接输出,放入后缀表达式中:
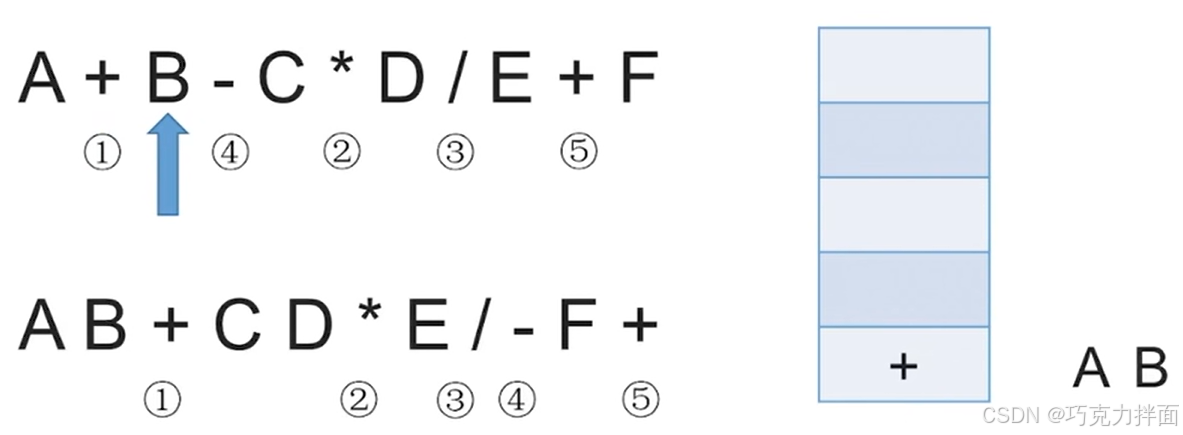
第四个数据为运算符-,但此时栈非空,所以当扫描到该运算符时需要依次弹出栈里优先级比当前运算符即-更高的或者等于的所有运算符,此时栈顶的运算符+和-优先级相同,所以把+弹出,放到后缀表达式里,最后再把当前扫描到的运算符即-入栈:
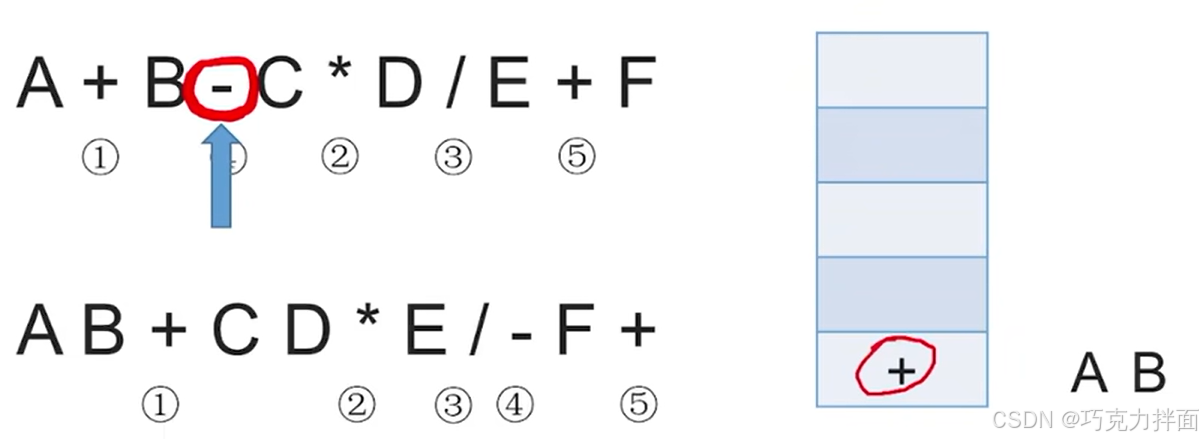
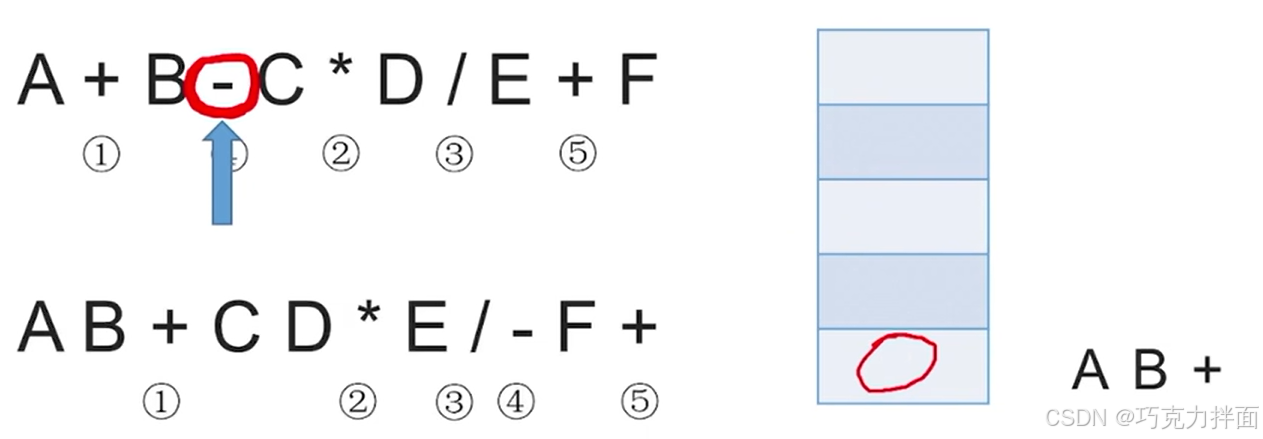
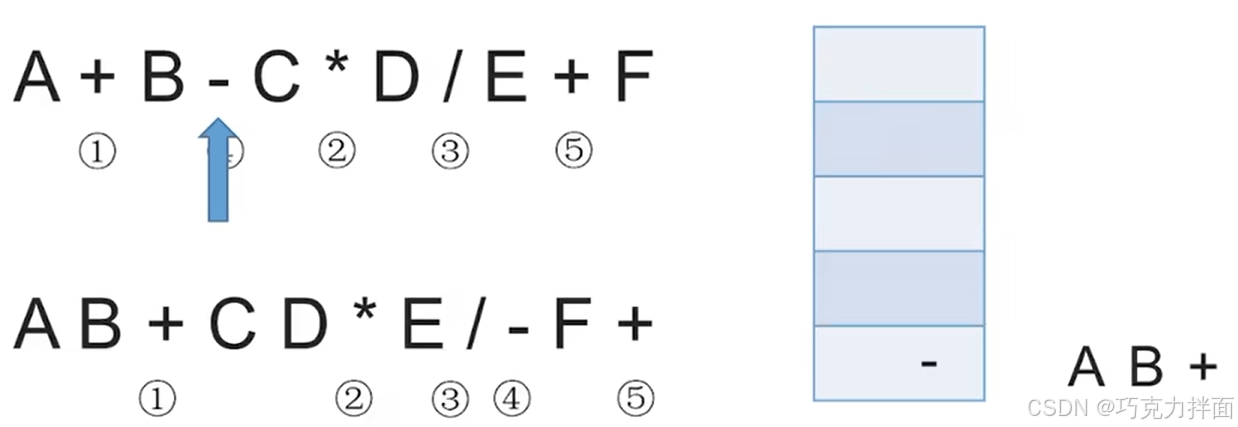
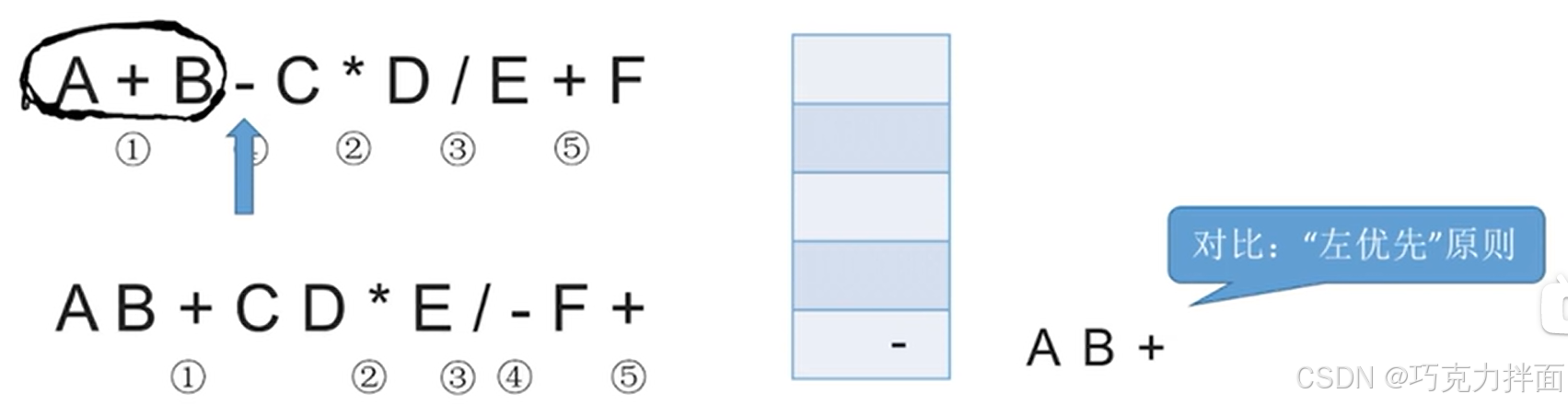
分析"依次弹出栈里优先级比当前运算符即-更高的或者等于的所有运算符"的底层逻辑:中缀表达式中如果出现一个操作数的话,除了第一个操作数和最后一个操作数,每一个操作数两边都有一个运算符,而且处理中缀表达式时是从左往右依次扫描的,所以之前栈里已经有一个+,然后+的后一个运算符就是-,就可以说明+和-之间就有一个操作数,所以扫描到-时就可以确定+和-之间的操作数既要进行+,也要进行-,而由于+和-的优先级相等,根据"左优先"原则,其实可以先执行+,所以可以先把+弹出栈,而且后缀表达式中运算符从左向右出现的顺序其实就是中缀表达式中运算符生效的顺序,所以先弹出+代表+先生效,既然+已经先生效了,此时中缀表达式中可以把A+B看作一个整体:
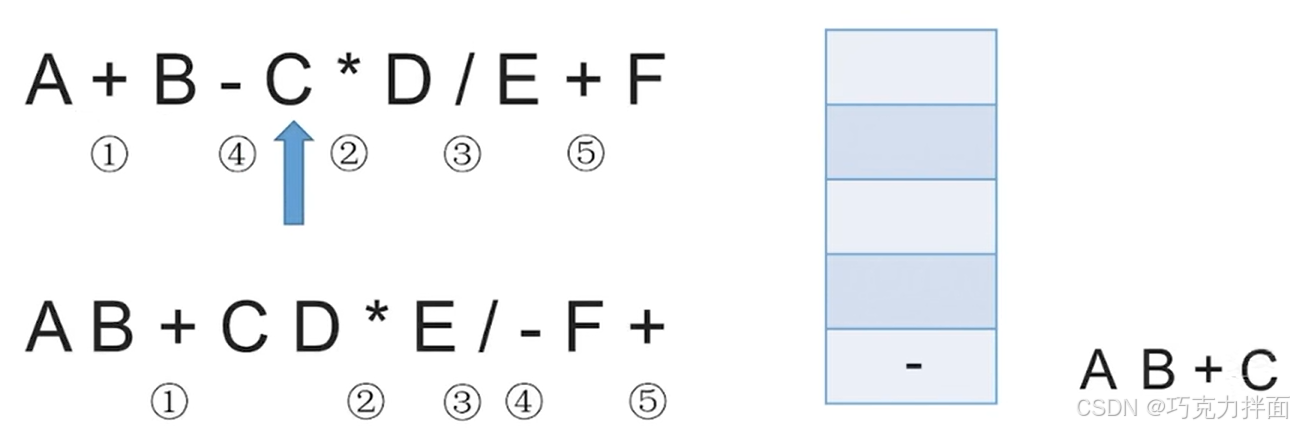
第五个数据为操作数C,因此直接输出,放入后缀表达式中:
第六个数据为运算符*,检查后发现栈顶元素是运算符-,这也就意味着当前扫描到的 * 的左边的操作数C的前面的运算符是-,由运算规则可知先*后-,所以-就不能弹出栈,因为如果-弹出栈之后就意味着-比 * 先生效,此时不符合运算规则,既然不能先算-,那么*能否先进栈再出栈放入后缀表达式呢?显然不行,因为 * 后面如果刚好出现了(),()要比 * 先生效,此时 * 弹出栈就意味着 * 比()先生效,不符合运算规则,因此此时无法确定能否先把 * 放入后缀表达式,所以需要把*放入栈中:
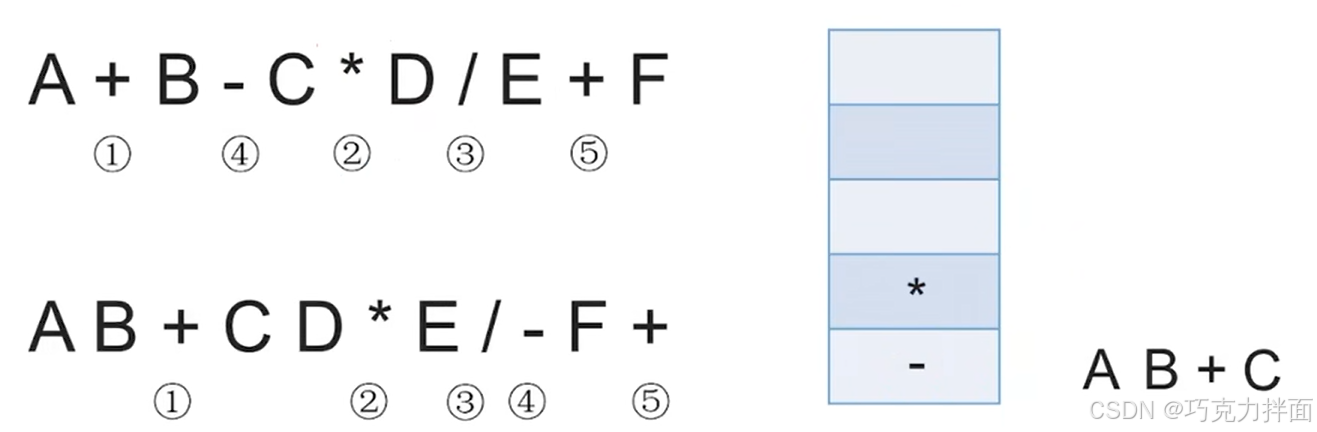
第七个数据为操作数D,因此直接输出,放入后缀表达式中:
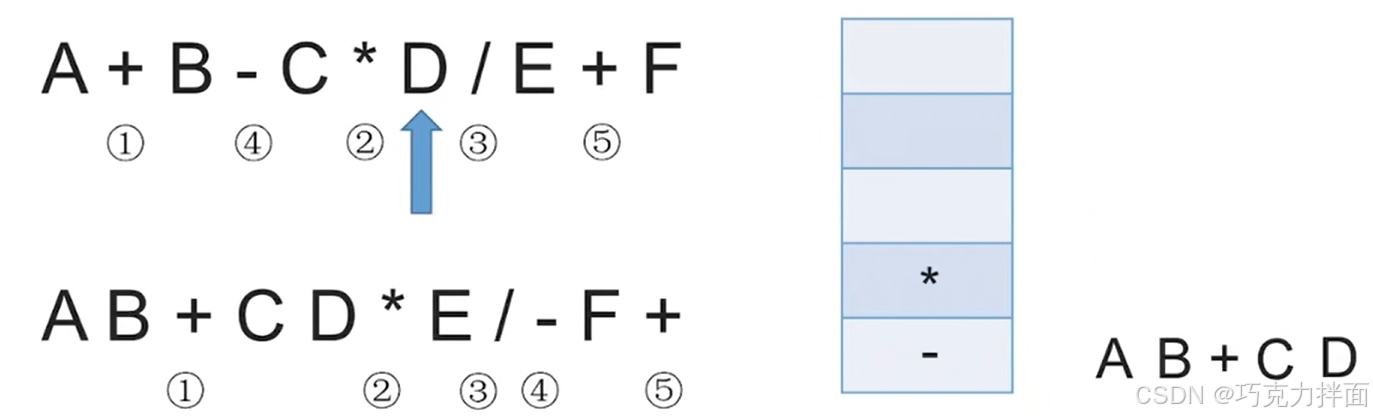
第八个数据为运算符/,此时检查栈发现栈顶元素为*,意味着/的左边的操作数D再左边的运算符为 *,当该操作数D既需要 * 也需要/时,由于 * 和/的优先级相等,此时就可以先让 * 生效,此时 * 就出栈,*生效后就意味着要把C * D看作一个整体,之前+也生效了即A+B也被看作了一个整体,此时再检查栈发现栈顶元素为-,说明/左边的操作数C * D再左边的运算符是一个运算符-,虽然/的优先级比-高,但由于无法确定/后面是否有(),所以/并不能先生效,因此/要入栈,不能出栈:
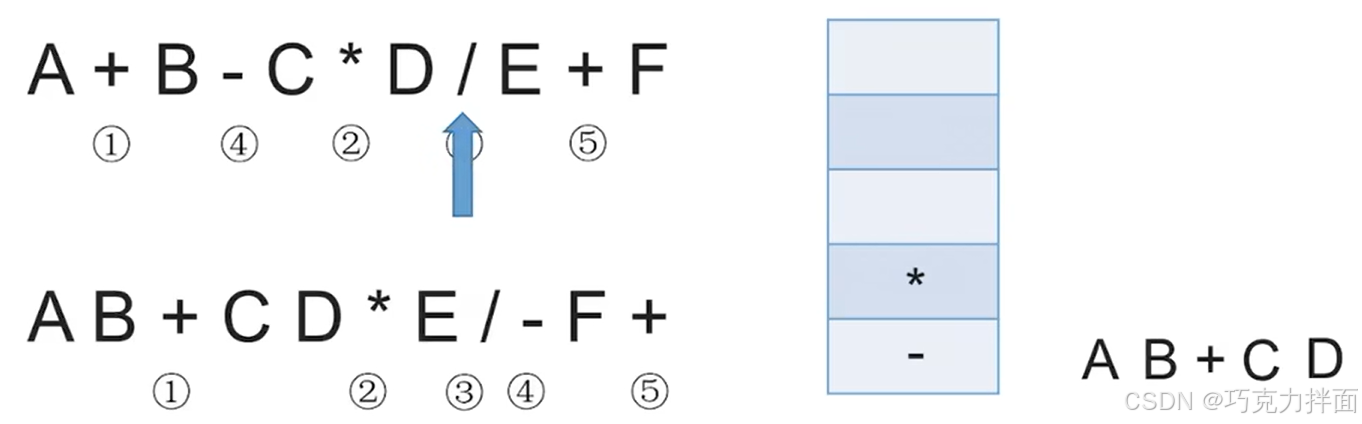
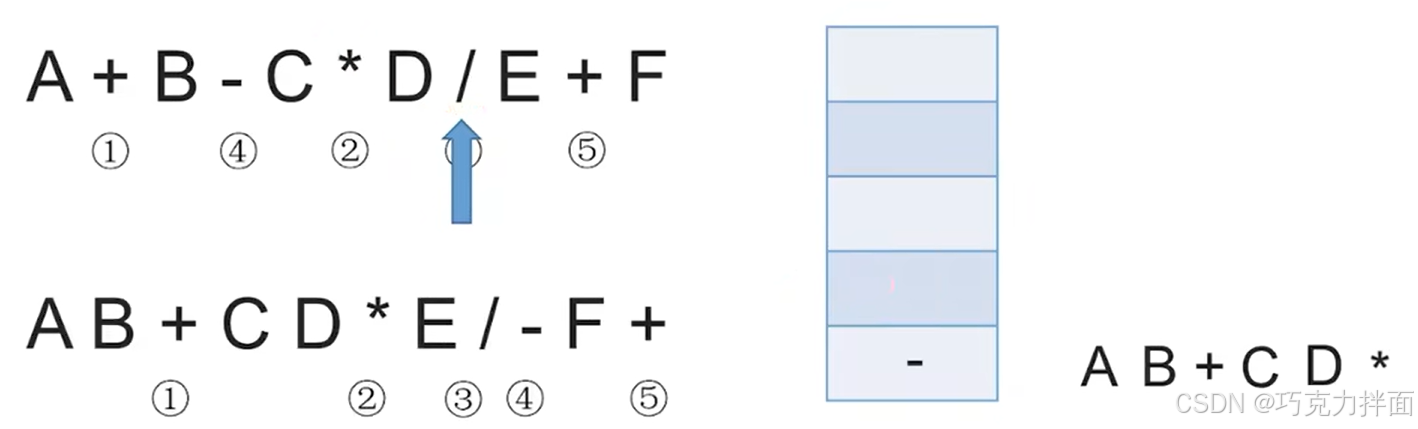
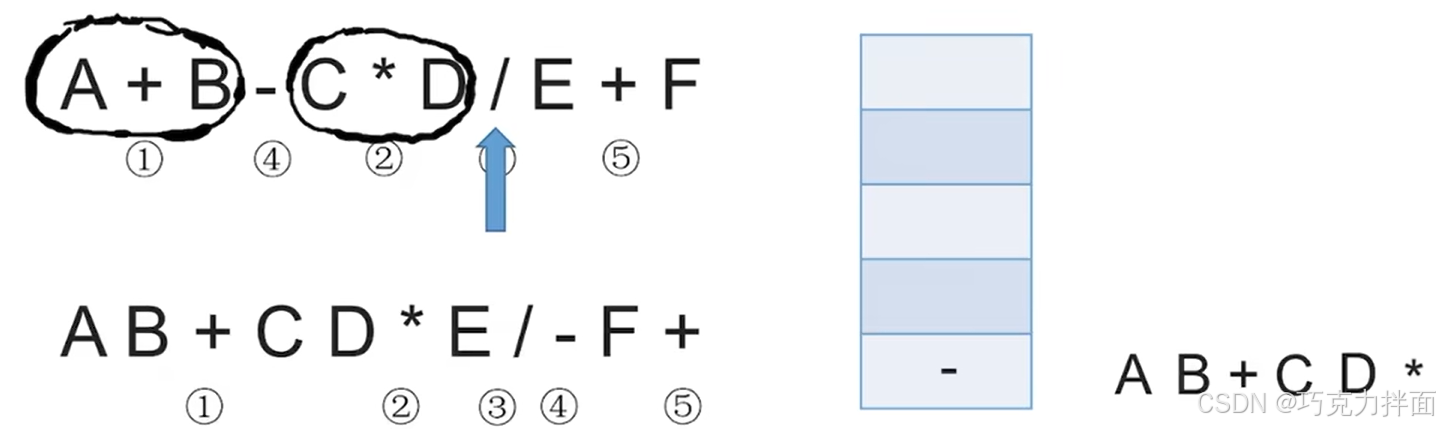
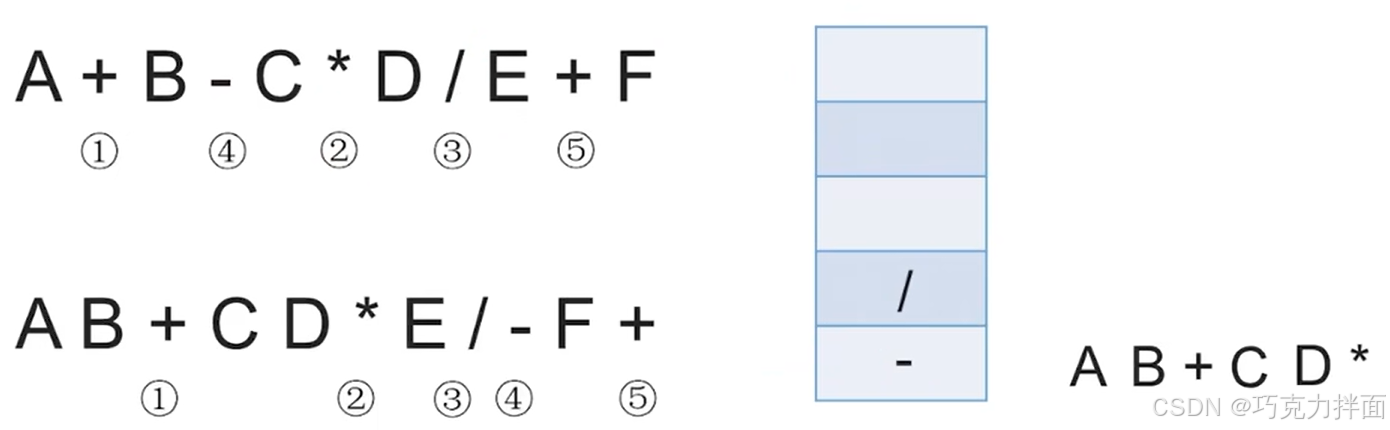
第九个数据为操作数E,因此直接输出,放入后缀表达式中:
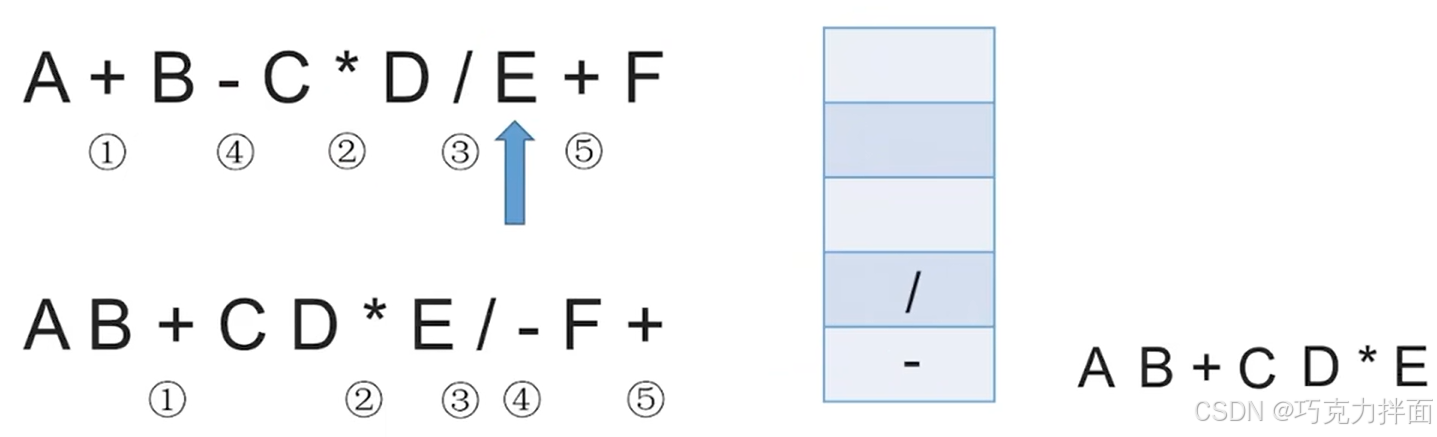
第十个数据为运算符+,检查栈发现栈顶元素为/,意味着+左边的操作数E再左边的运算符为/,操作数E既要/也要+,此时就可以确定应该让操作数E的/先生效,因为/的优先级大于+,所以/出栈,/出栈意味着/生效,因此就需要把C * D / E看作一个整体,继续检查栈发现栈顶元素为-,意味着+左边的操作数C * D / E再左边的运算符是-,而当C * D / E既需要-也需要+时,按照"左优先"原则可以先让左边的运算符-生效,因此-出栈,放入后缀表达式中:
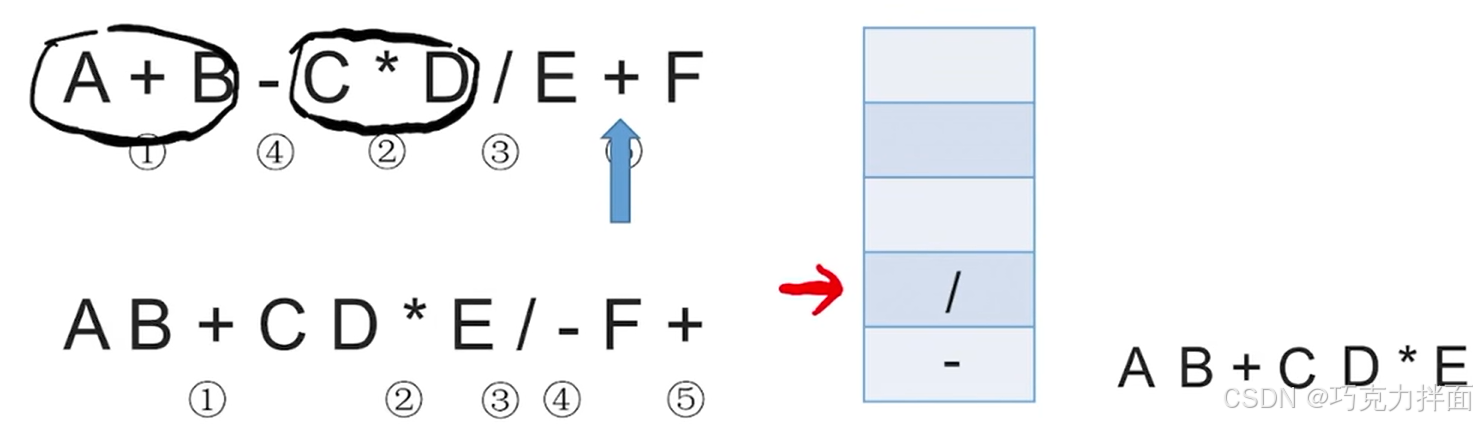
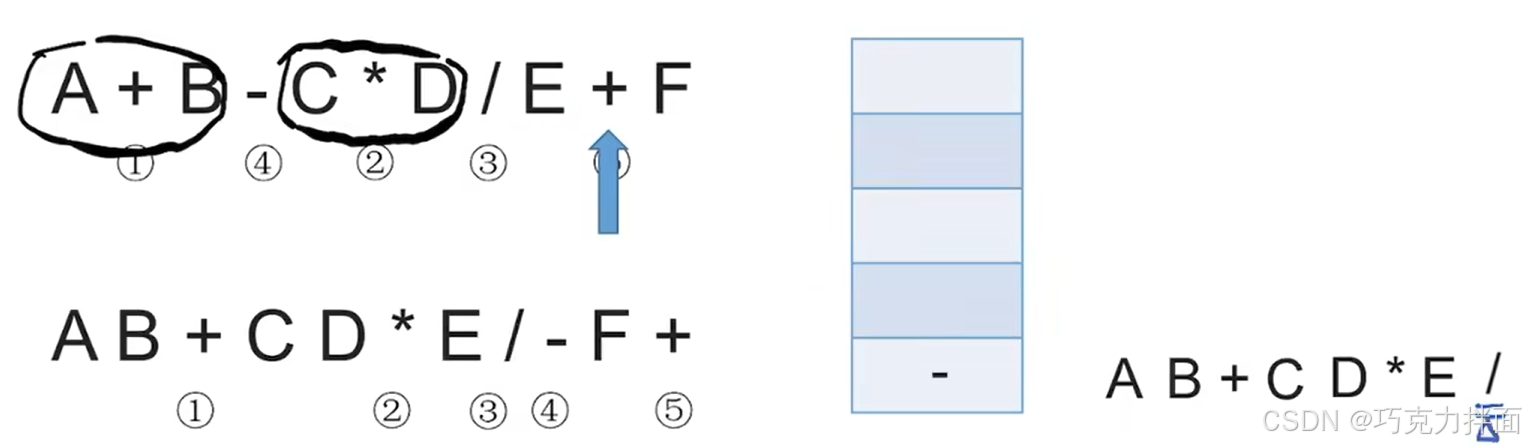
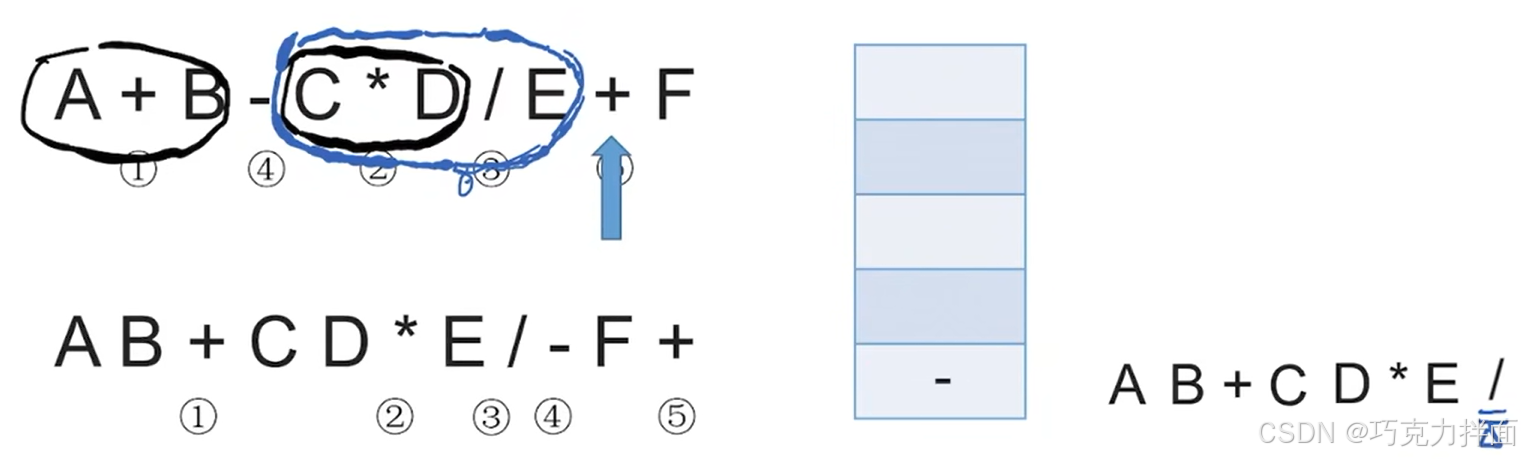
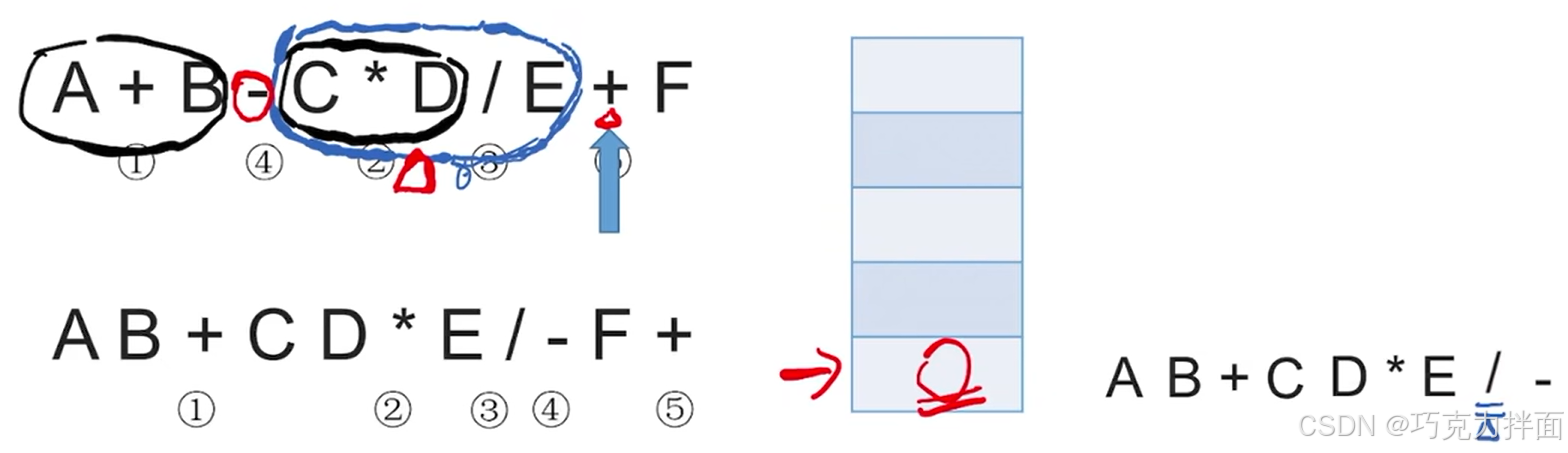
第十一个数据为操作数F,因此直接输出,放入后缀表达式中:
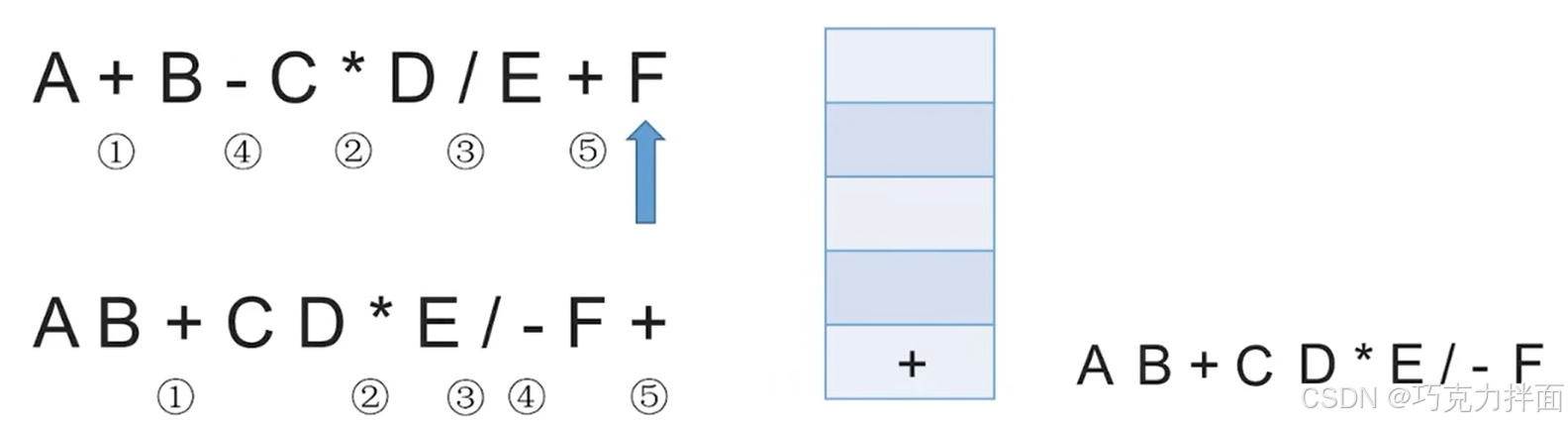
此时中缀表达式里的所有字符全部处理完毕,把栈里剩余的全部运算符依次弹出,放入后缀表达式中:
例二:带有界限符即()
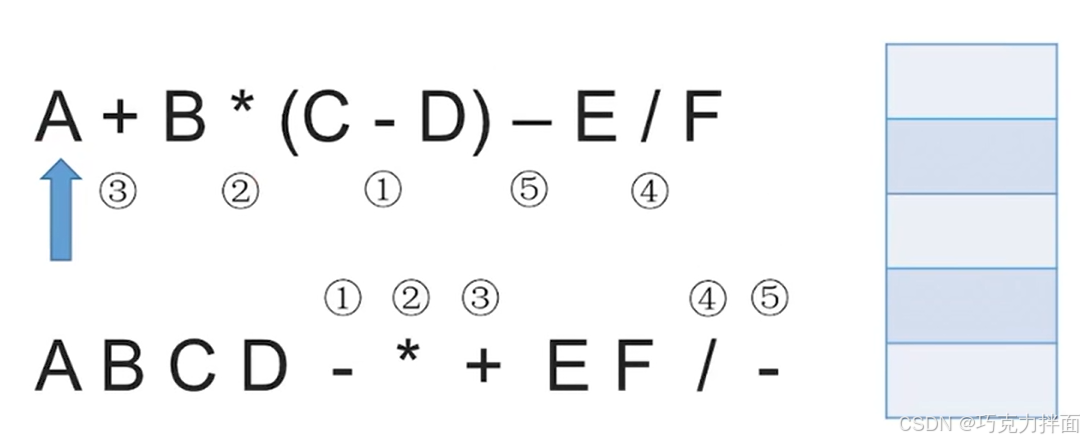
从左往右开始扫描中缀表达式,第一个数据为操作数A,因此直接输出,放入后缀表达式中:
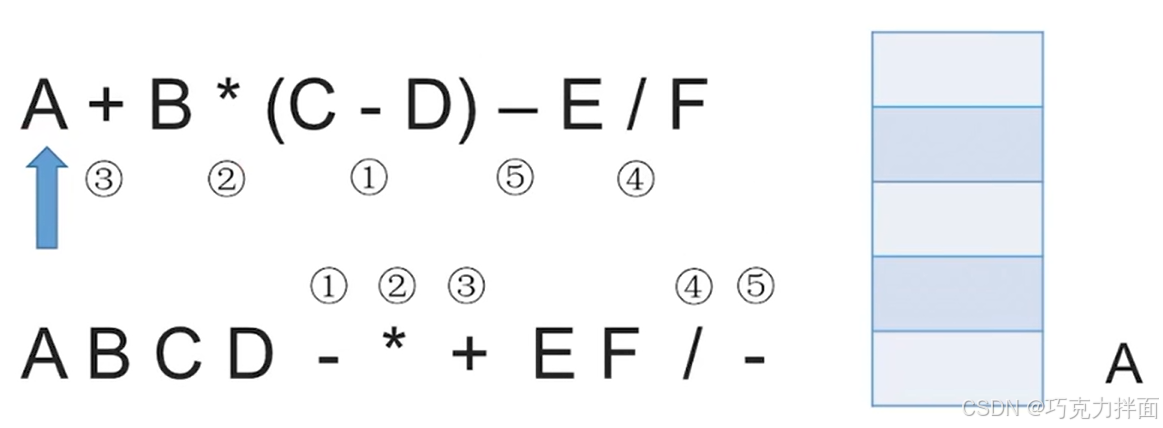
第二个数据为运算符+,此时栈空,因此入栈:
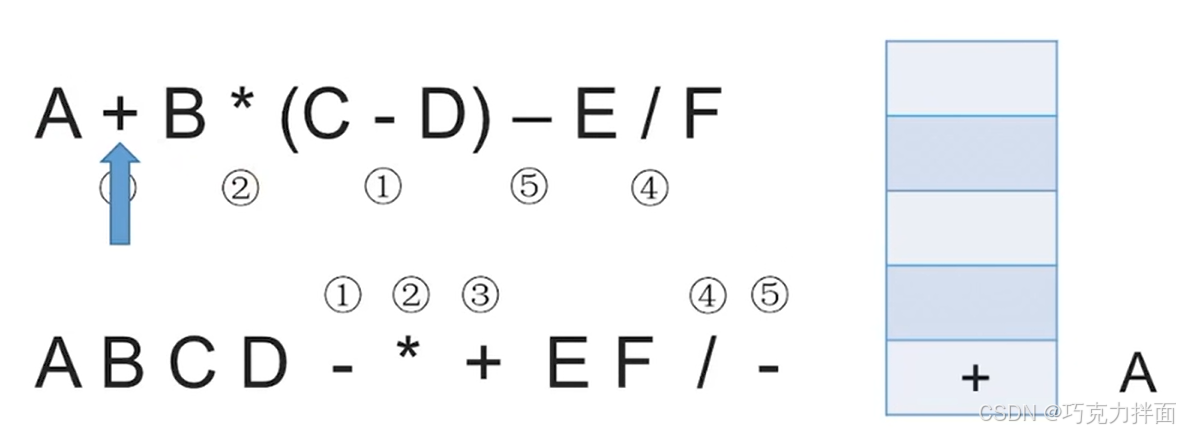
第三个数据为操作数B,因此直接输出,放入后缀表达式中:
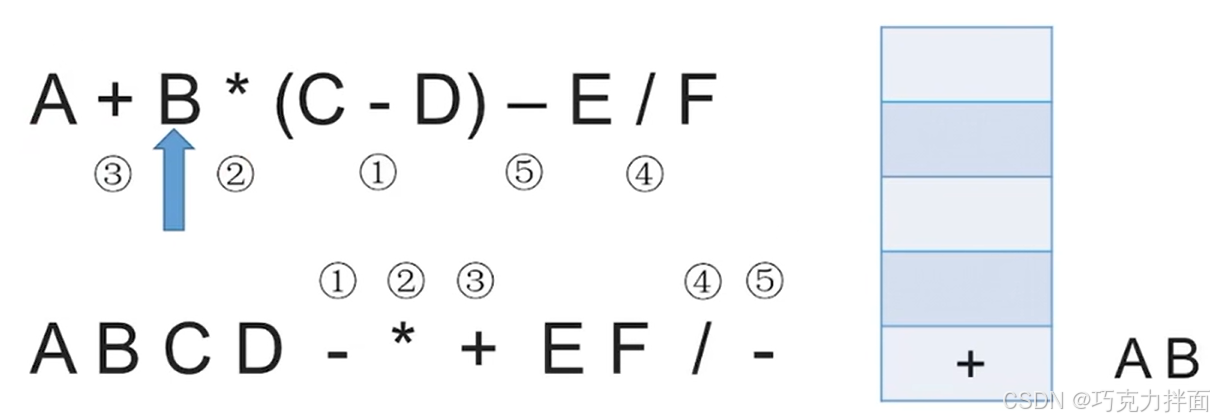
第四个数据为运算符*,由于栈顶此时只有+,+的优先级低于 *,所以 * 直接入栈:
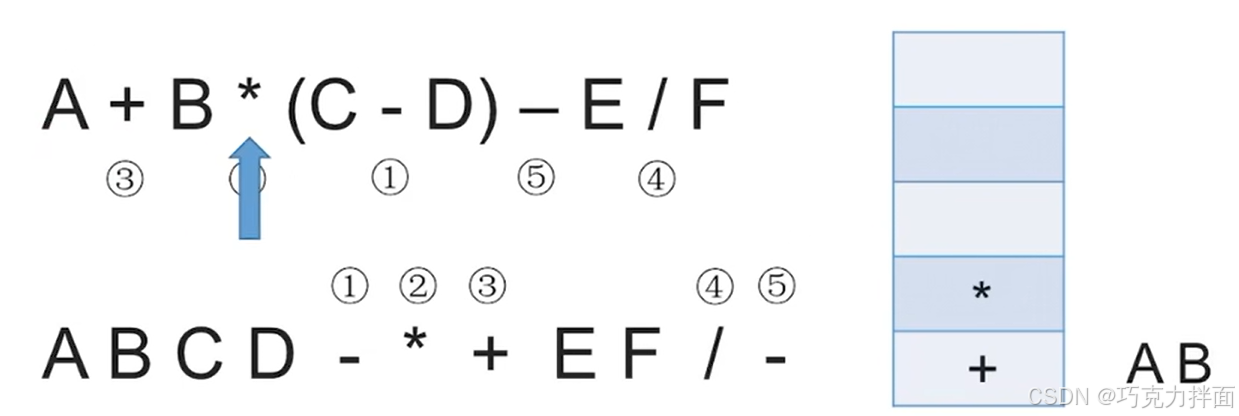
第五个数据为界限符(即左括号,直接入栈:
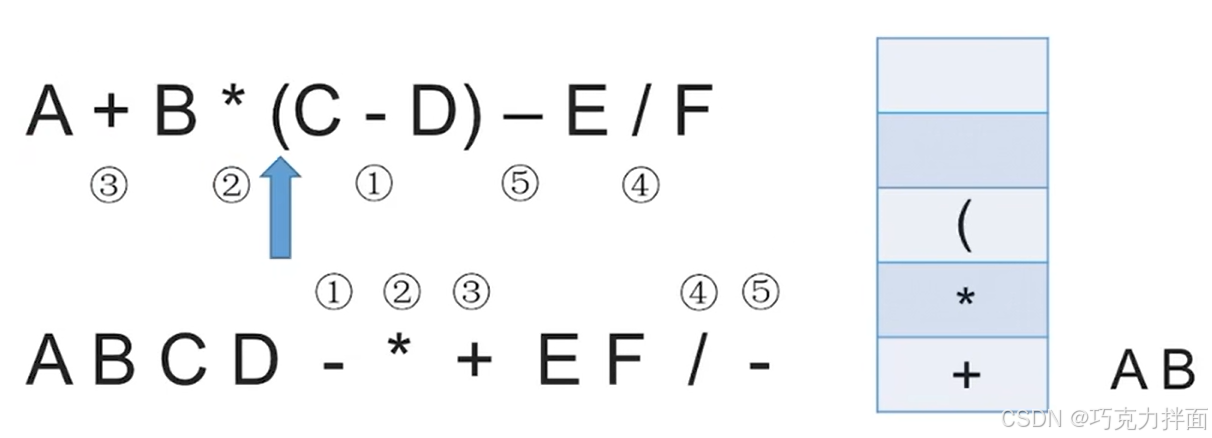
第六个数据为操作数C,因此直接输出,放入后缀表达式中:
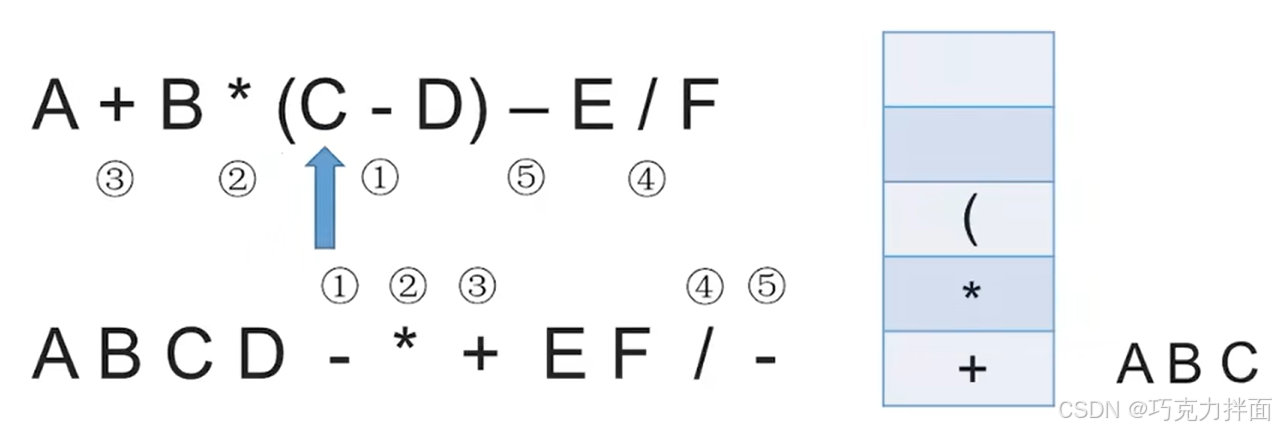
第七个数据为运算符-,由于此时栈顶是(,因此不需要弹出任何元素,直接-入栈,原因是如果栈顶是左括号(,那么说明-左边的操作数它的左边有一个(,虽然要优先计算括号里的运算,但是由于扫描到-时还不能确定-右边的操作数它的右边是否有比-优先级更高的运算符如 * ,因此此时无法确定-是否能立即生效,因此-入栈后其他元素不能出栈:
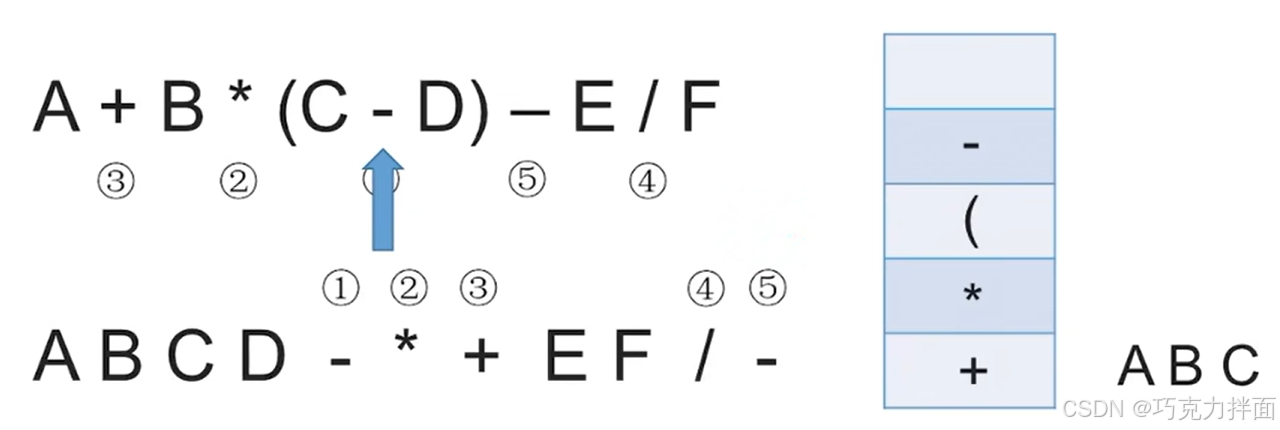
第八个数据为操作数D,因此直接输出,放入后缀表达式中:
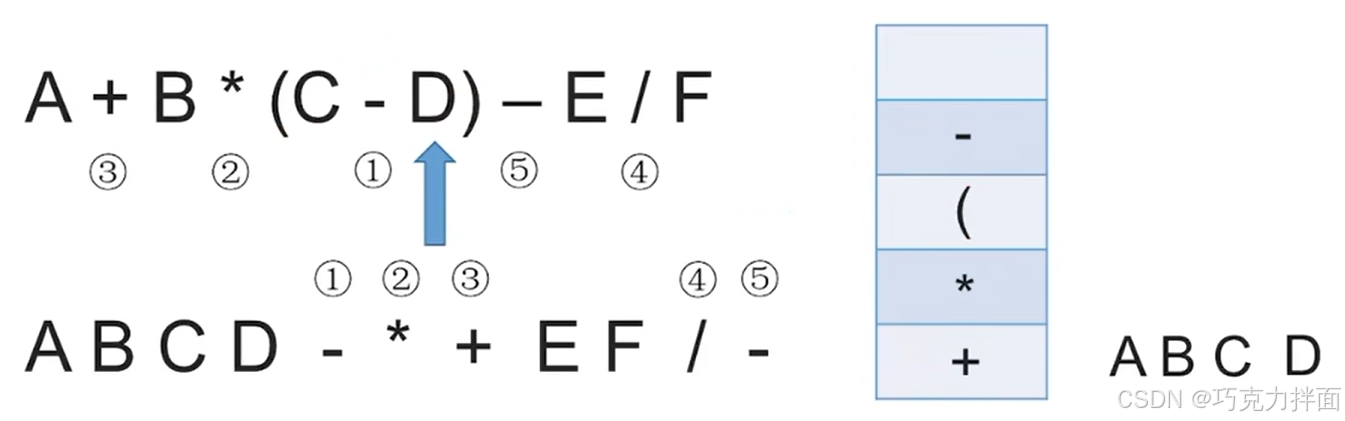
第九个数据为界限符右括号),当遇到右括号)时,需要依次弹出栈内所有运算符并加到后缀表达式中,直到弹出左括号(为止,注:左括号弹出后是不需要加到后缀表达式中的,因为后缀表达式是没有界限符的,底层逻辑是扫描到右括号)时,此时可以确定整个括号的范围,由于需要优先计算括号内的内容,那么就可以把括号内的运算符全部弹出,就意味着括号内的全部运算都可以先生效:
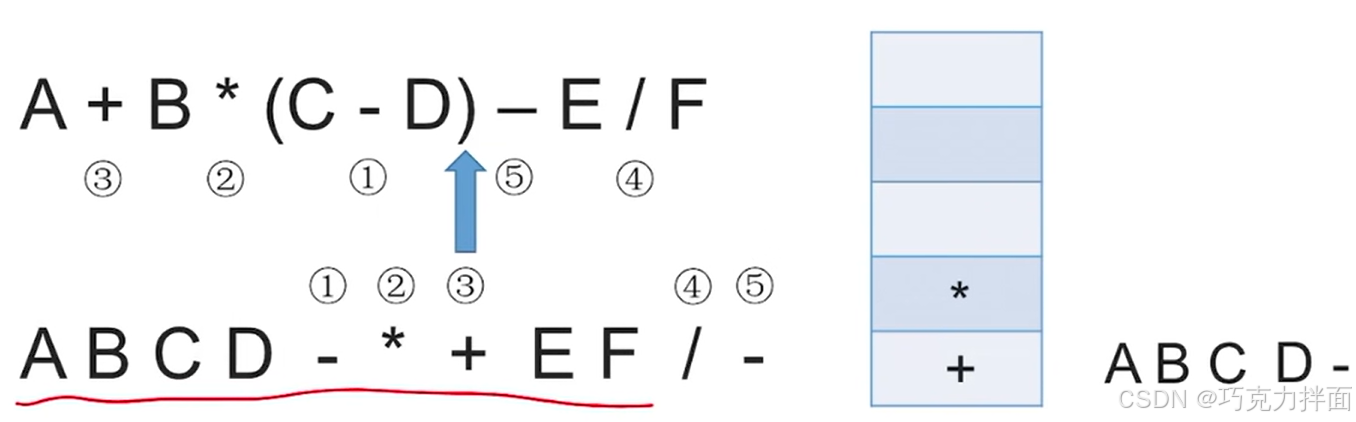
第十个数据为运算符-,根据规则可知,需要把栈里的 * 和+都依次弹出,因为 * 优先级高于-,+优先级等于-,然后再把新扫描到的-压入栈:
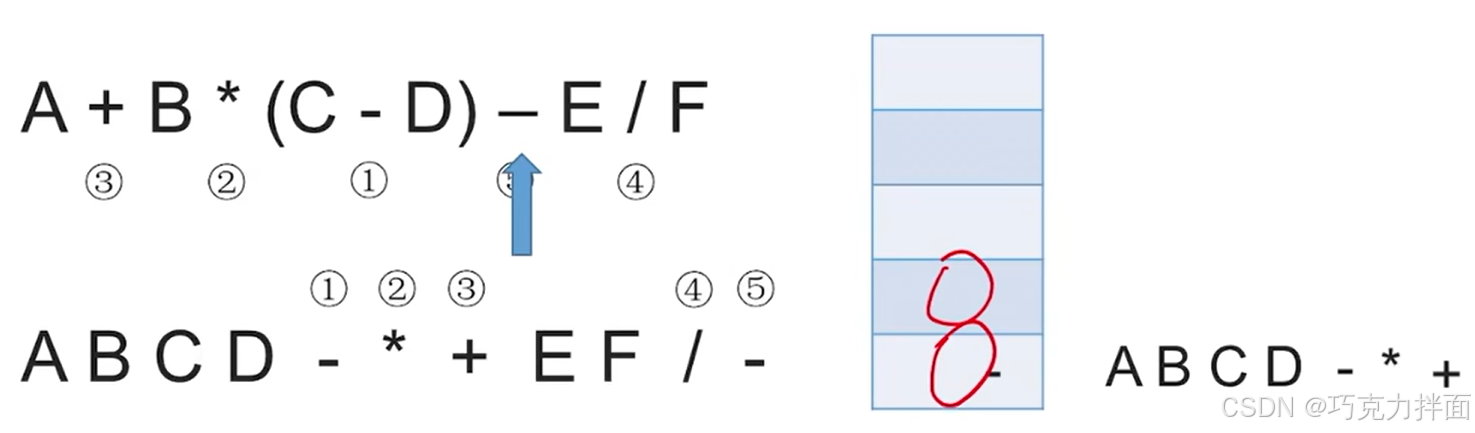
第十一个数据为操作数E,因此直接输出,放入后缀表达式中:
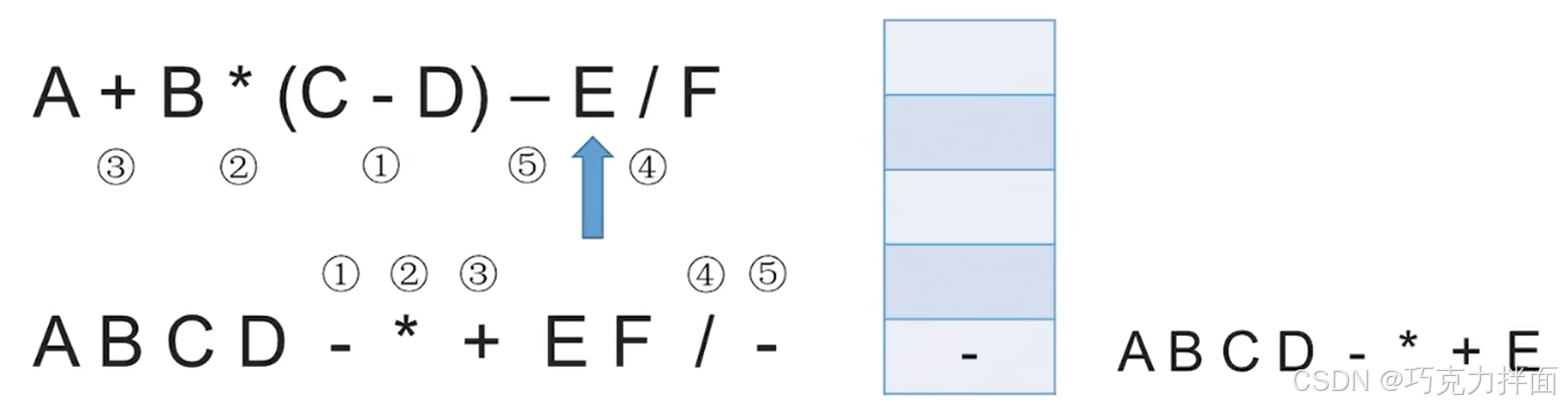
第十二个数据为运算符/,由于/的优先级要比栈顶的-高即此时栈中没有比/优先级高或者等于的运算符,所以/直接入栈:
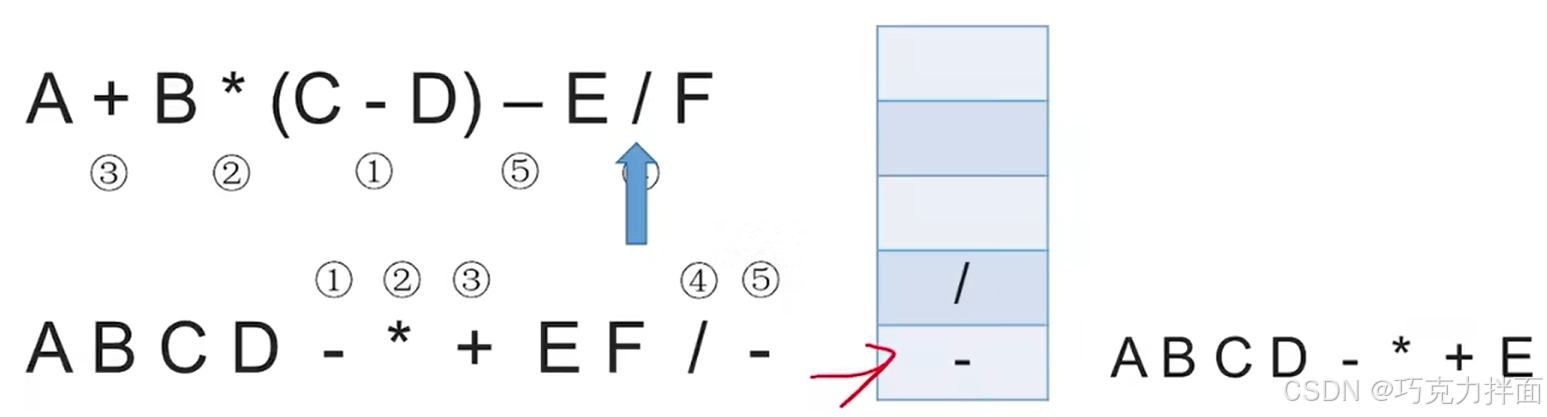
第十三个数据为操作数F,因此直接输出,放入后缀表达式中:
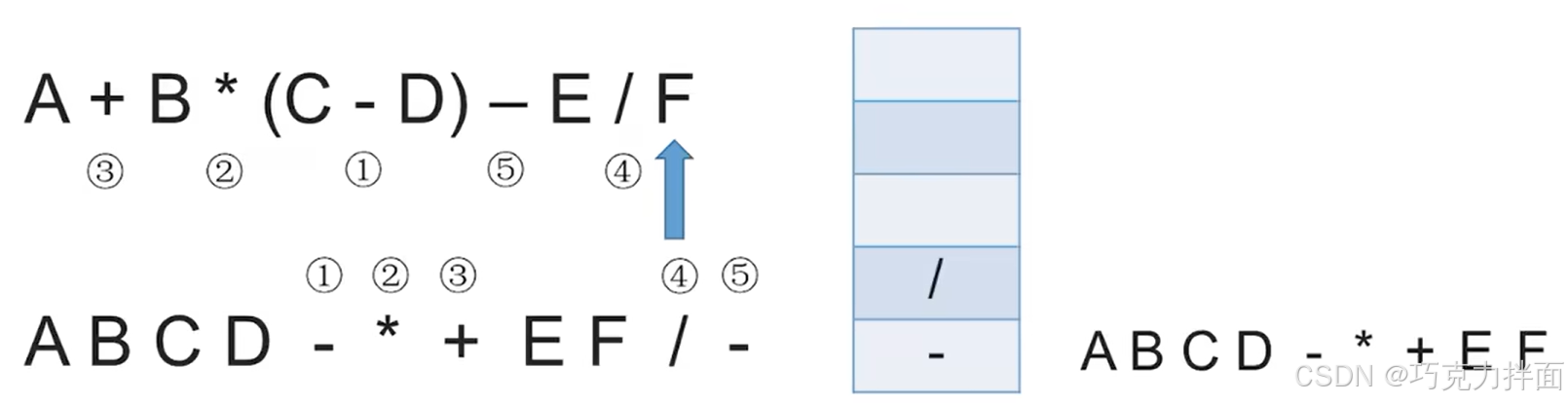
此时所有字符全部处理完毕,接下来依次弹出栈里的元素,加到后缀表达式中:
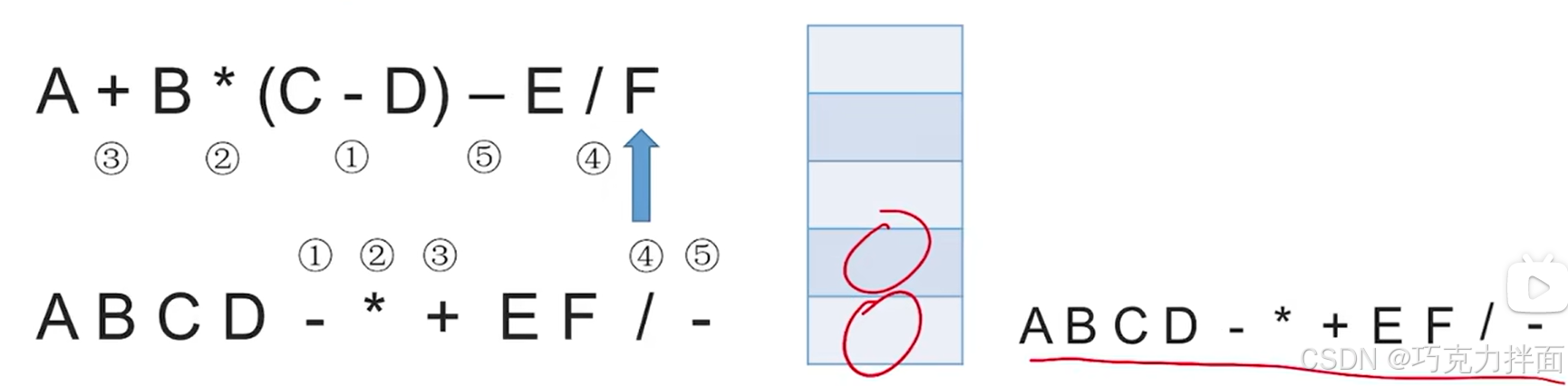
3.注意事项:

八.利用栈实现中缀表达式的计算:


中缀表达式转后缀表达式和后缀表达式的计算都是从左向右扫描,因此中缀表达式转后缀表达式和后缀表达式的计算可以同时进行,即一边生成后缀表达式,一边计算已生成的后缀表达式
1.实例:

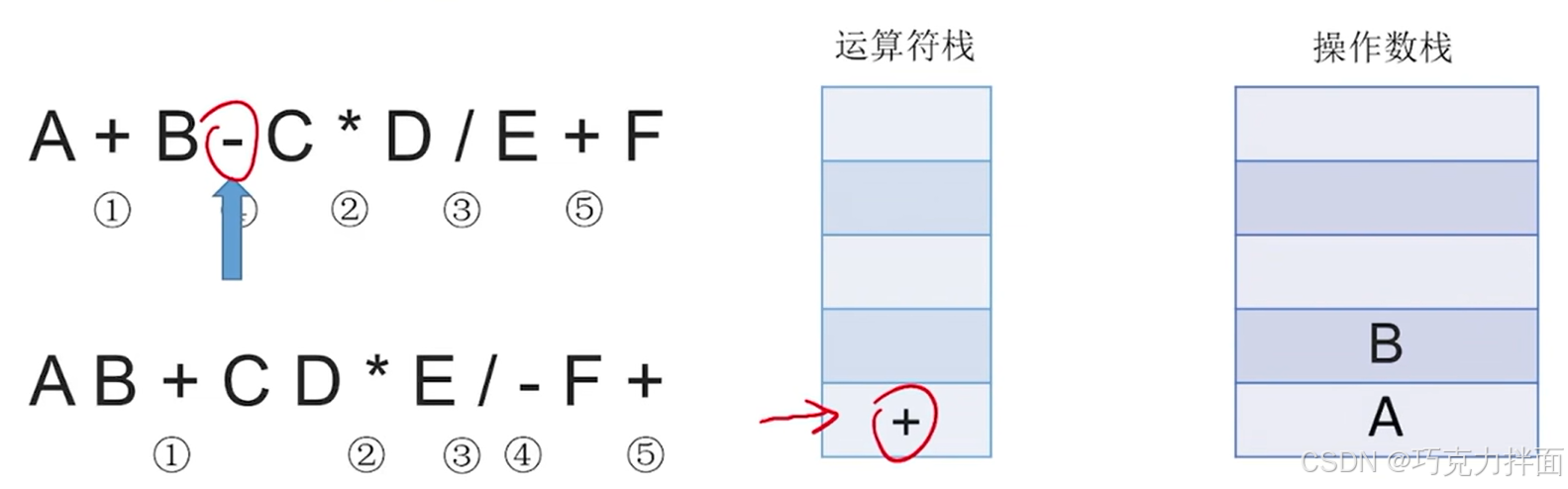
从左往右扫描中缀表达式A + B - C * D / E + F,扫描到的第一个数据为操作数A,因此压入操作数栈:
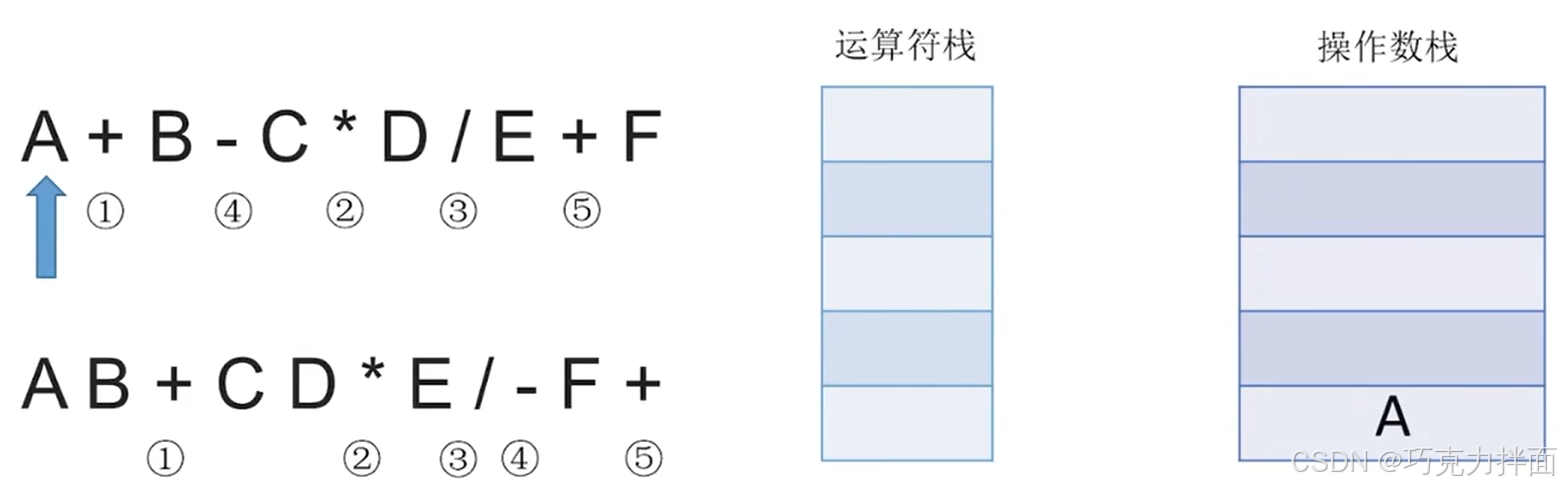
扫描到的第二个数据为运算符+,根据"中缀表达式转后缀表达式"的规则可知,+压入运算符栈:
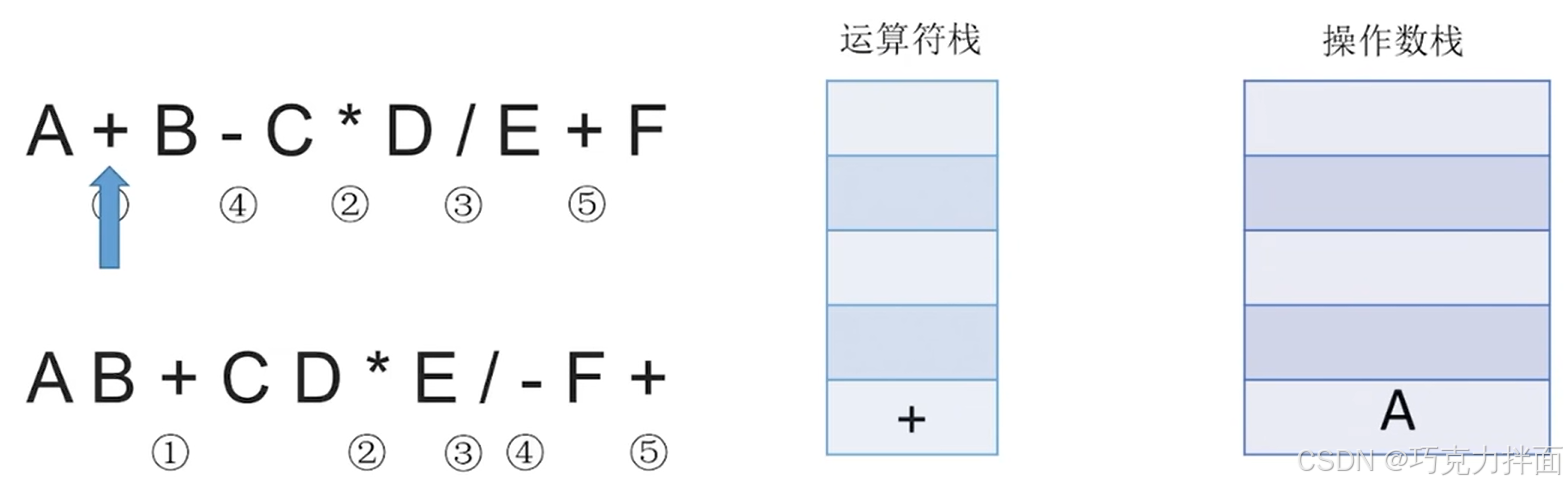
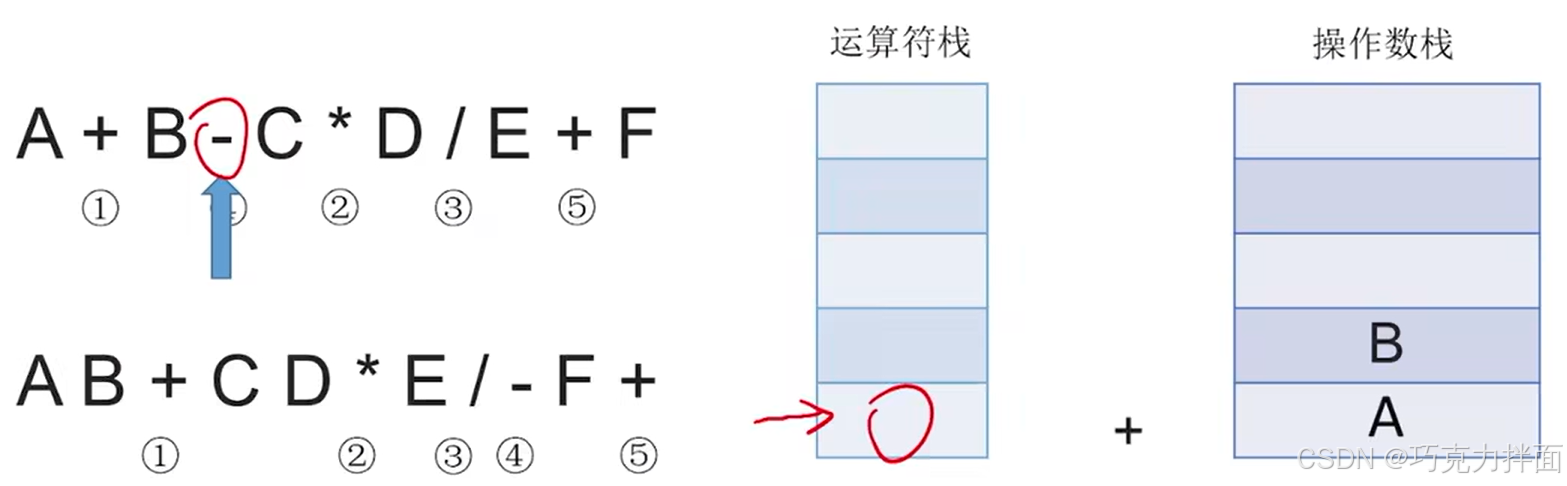
扫描到的第三个数据为操作数B,因此压入操作数栈:
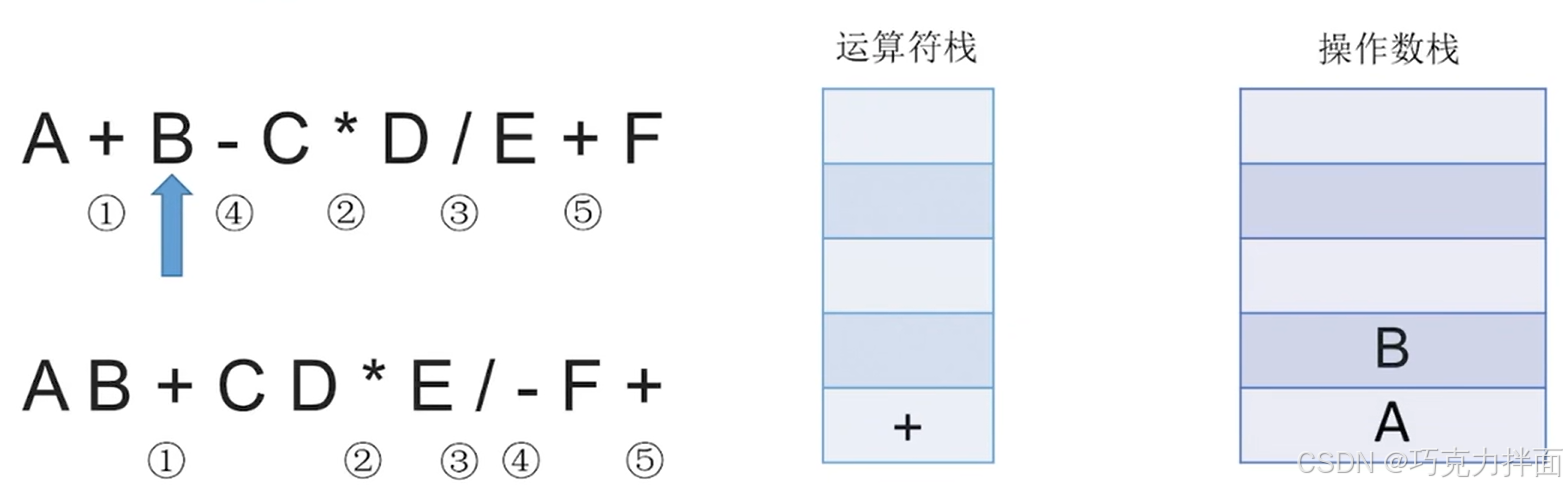
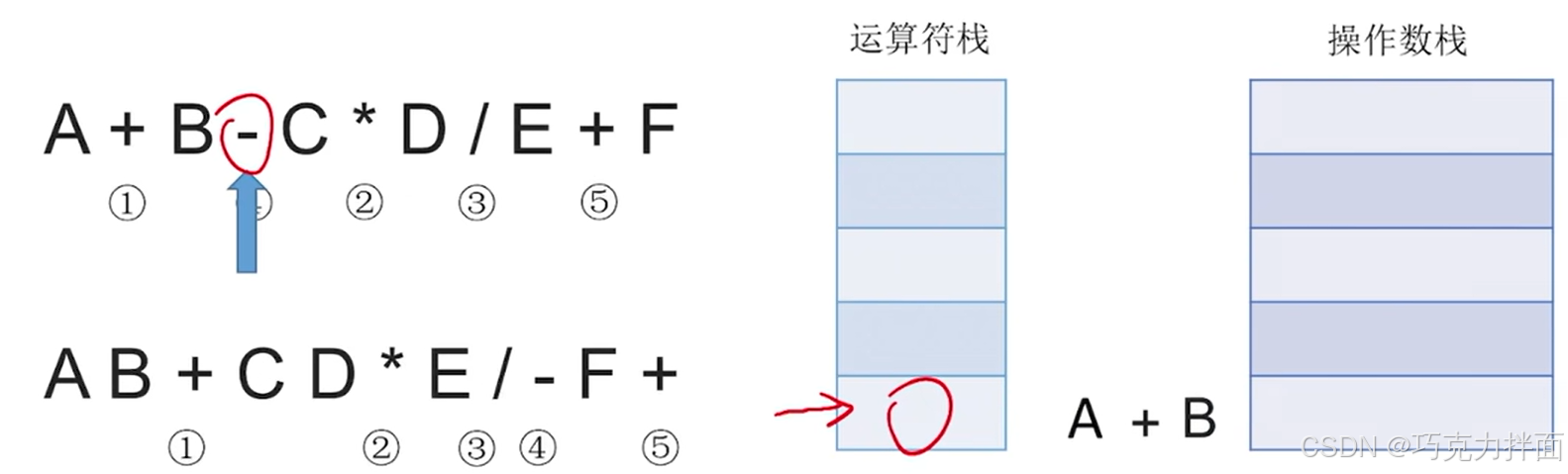
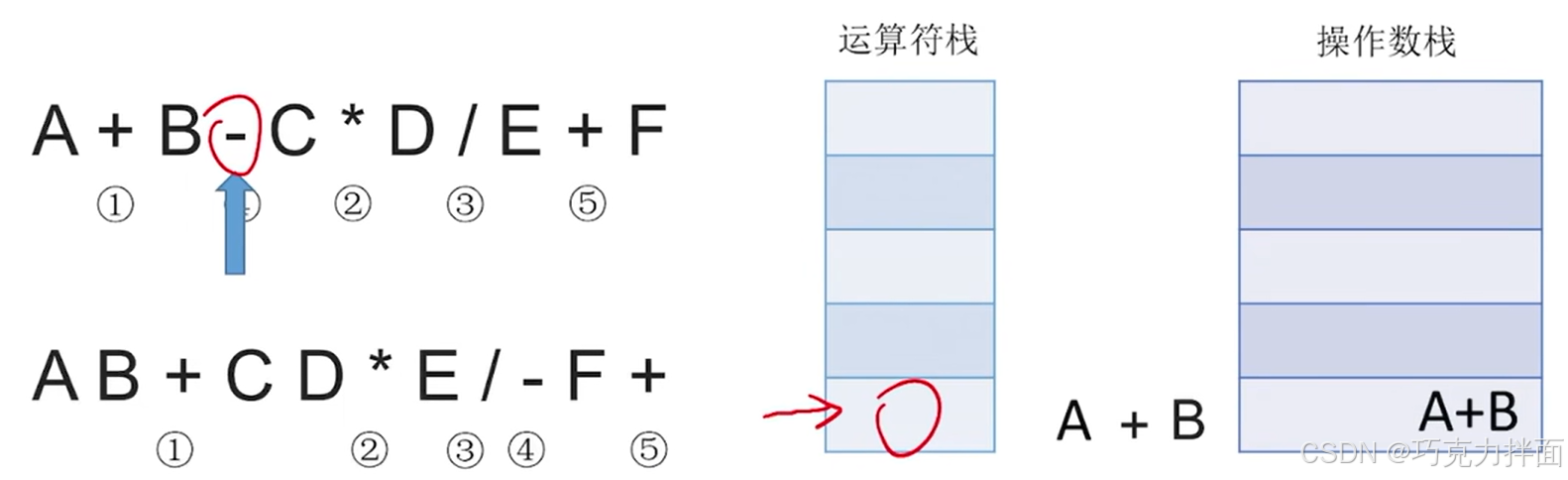
扫描到的第四个数据为运算符-,此时运算符栈顶的运算符+和运算符-的优先级相等,因此需要把+弹出运算符栈,注:把一个运算符弹出运算符栈意味着已经确定该运算符先生效,所以在弹出一个运算符时就需要再弹出两个操作数栈的栈顶元素并执行相应运算,之后运算结果再压入操作数栈,最后新扫描到的运算符压入运算符栈:操作数栈中先弹出的元素作为右操作数,后弹出的元素作为左操作数
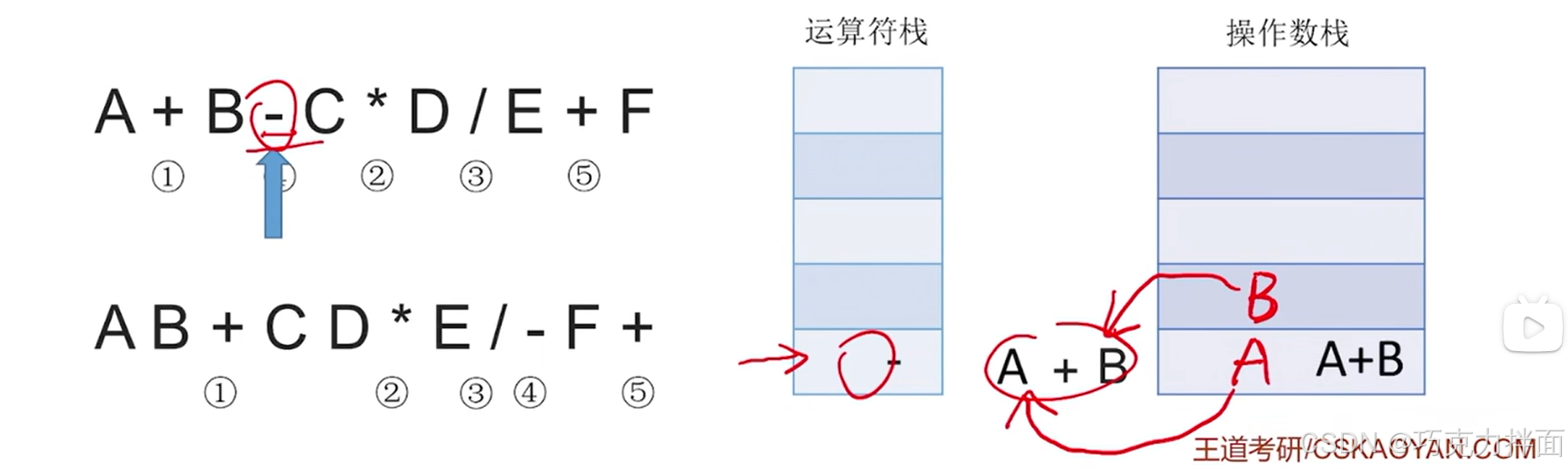
扫描到的第五个数据为操作数C,因此压入操作数栈:
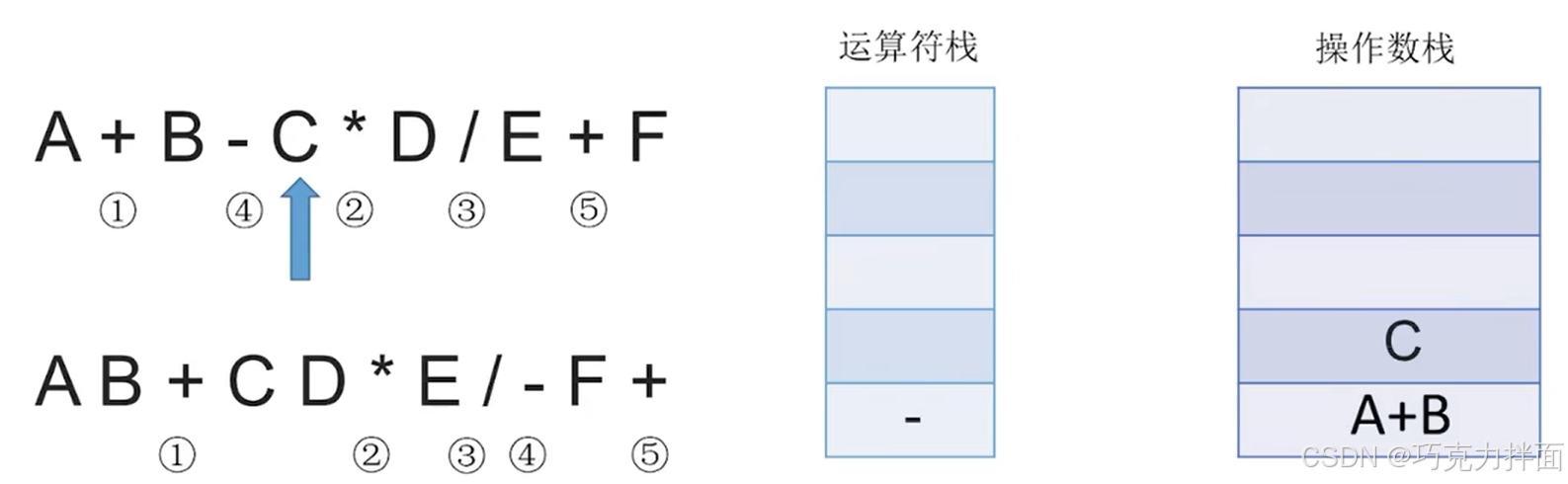
扫描到的第六个数据为运算符*,由于 * 的优先级比-高即运算符栈里没有高于或者等于 * 的运算符,所以-无需出运算符栈,直接 * 入运算符栈即可:
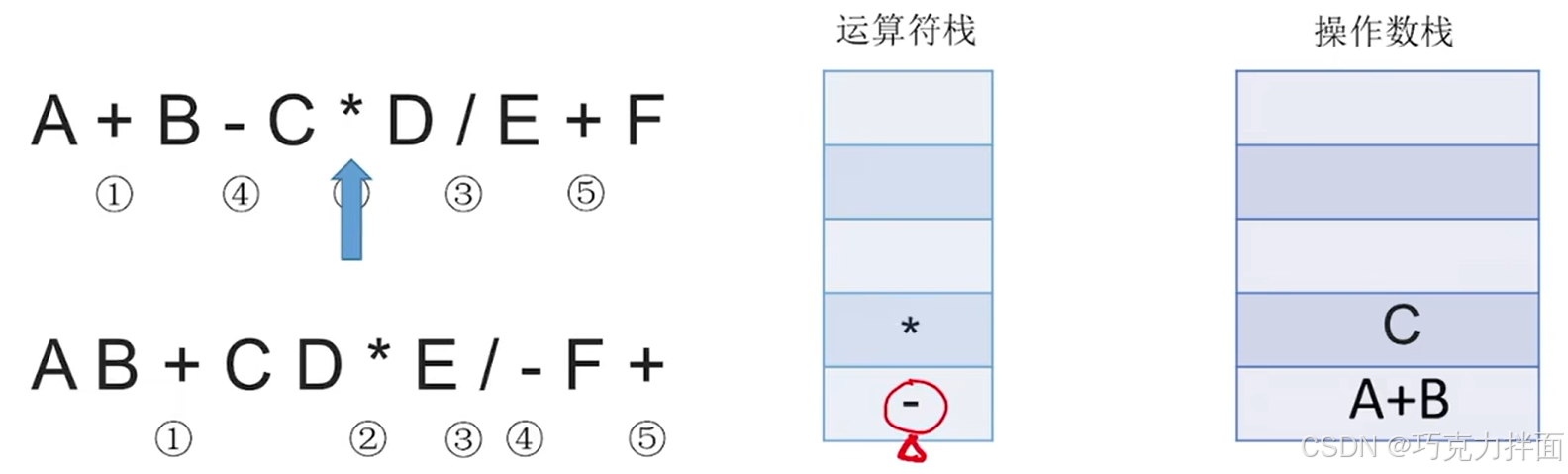
扫描到的第七个数据为操作数D,因此压入操作数栈:
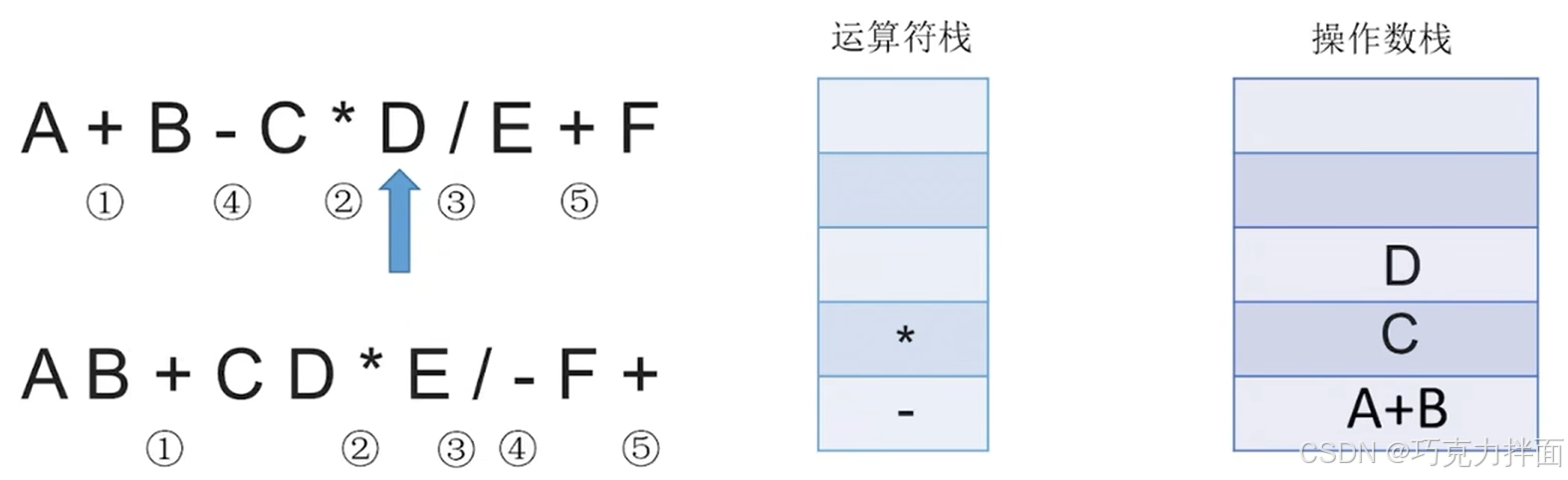
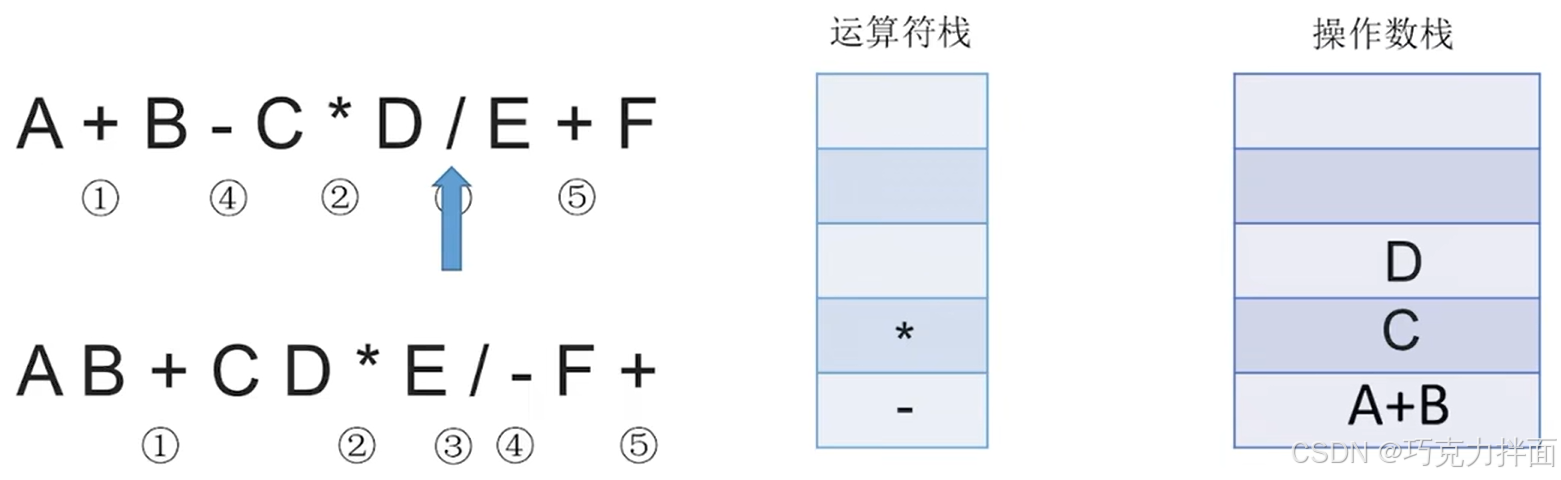
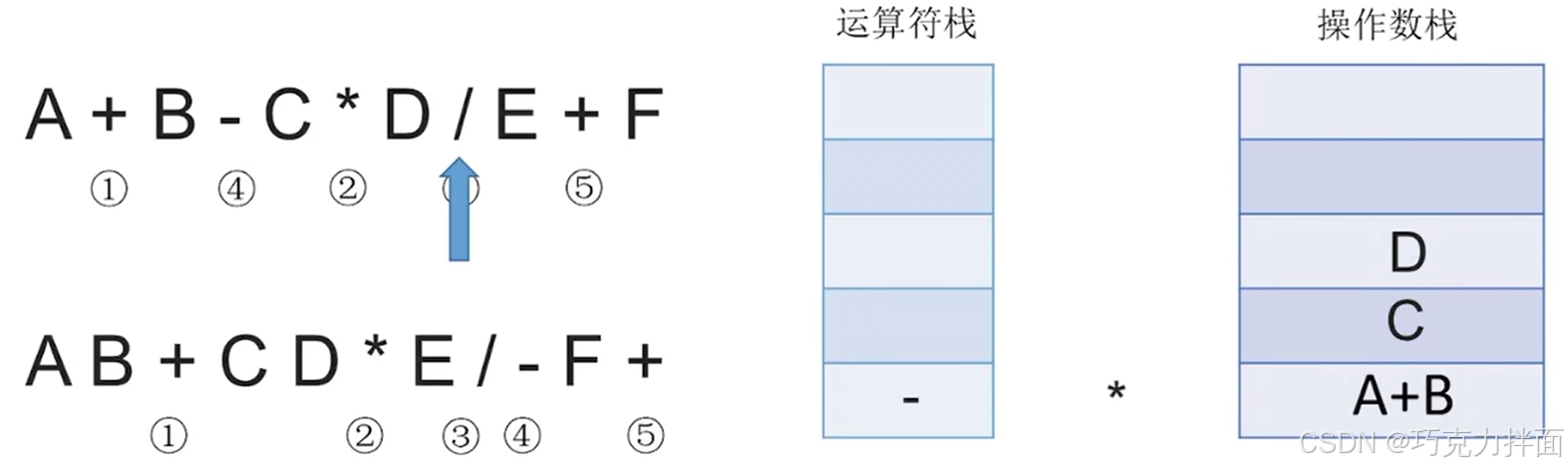
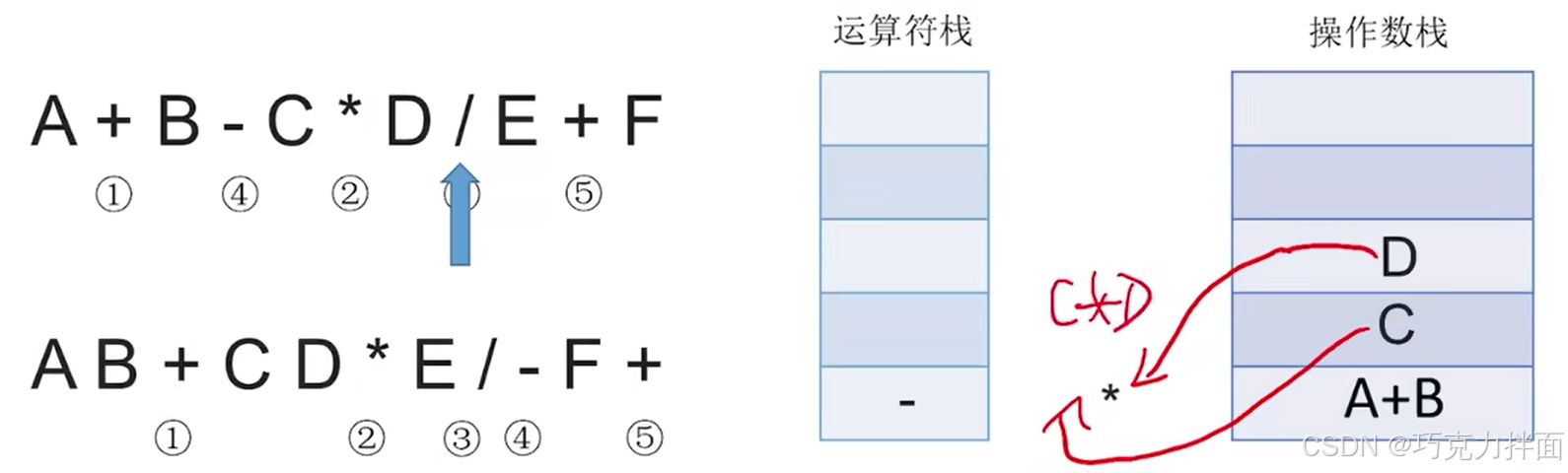
扫描到的第八个数据为运算符/,根据"中缀表达式转后缀表达式"的规则,此时需要把*弹出运算符栈(-的优先级低于/,因此-不出运算符栈),此时弹出一个运算符就需要操作数栈中弹出两个栈顶元素与该运算符生效,最终运算结果再压入操作数栈,新扫描到的运算符/压入运算符栈:
扫描到的第九个数据为操作数E,因此压入操作数栈:
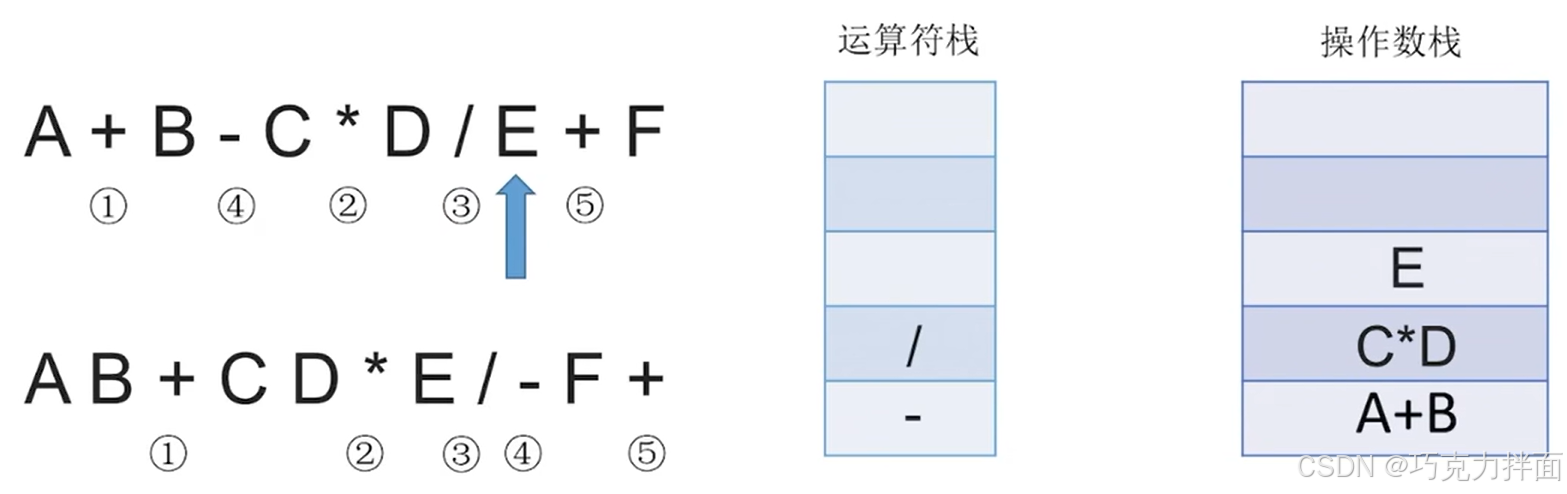
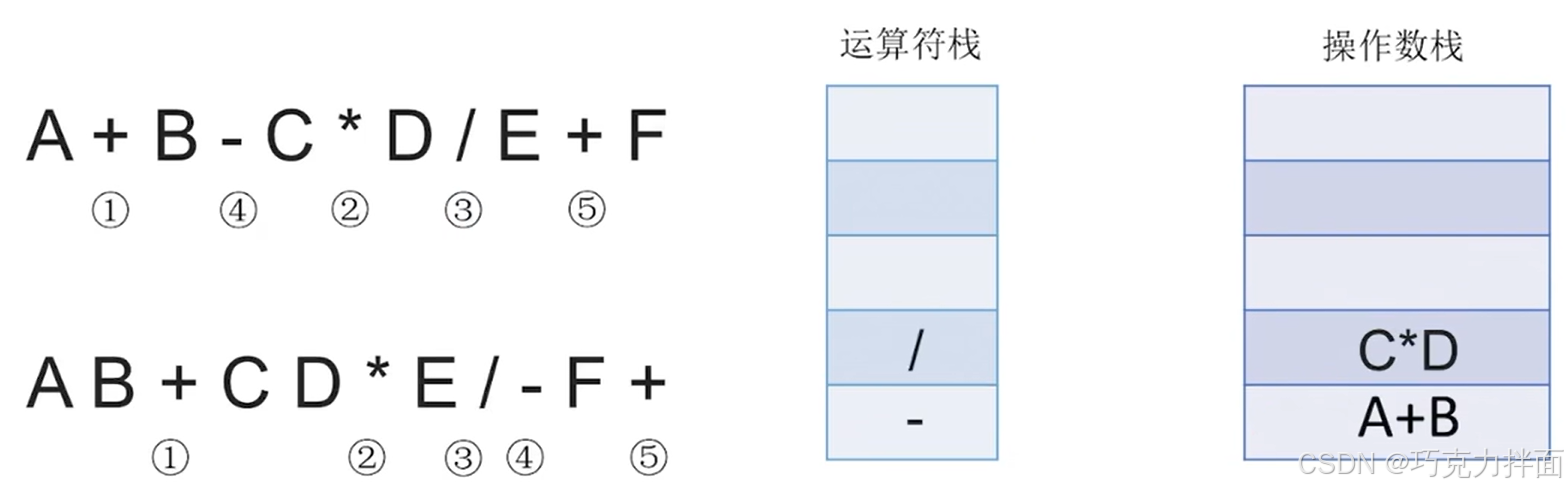
扫描到的第十个数据为运算符+,根据"中缀表达式转后缀表达式"的规则,此时需要把/(/优先级高于+)和-(-优先级等于+)都依次弹出运算符栈,先弹出/即/先生效,此时操作数栈需要弹出E和C * D,/生效的结果为(C * D)/E,再把(C * D)/E压入操作数栈顶,此时操作数栈里已经没有E和C * D了,再把-弹出运算符栈,-生效的结果为(A+B)- (C * D)/E,再把(A+B)- (C * D)/E压入操作数栈,此时操作数栈里已经没有(A+B)和(C * D)/E了,最后再把当前扫描到的运算符+压入运算符栈顶中:
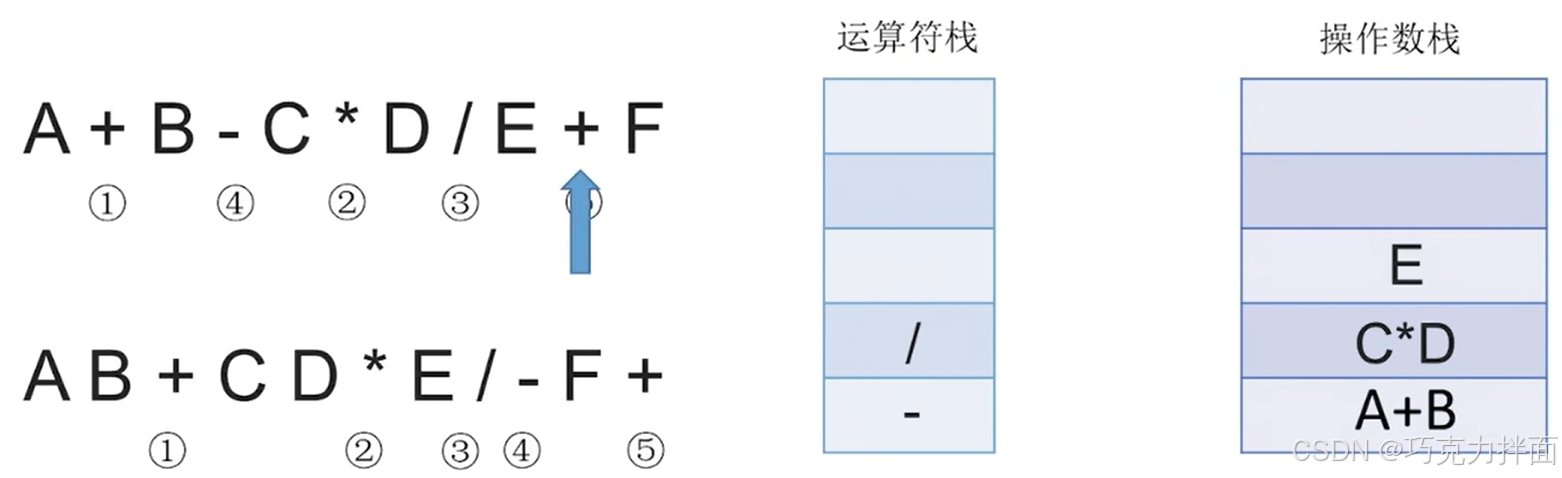
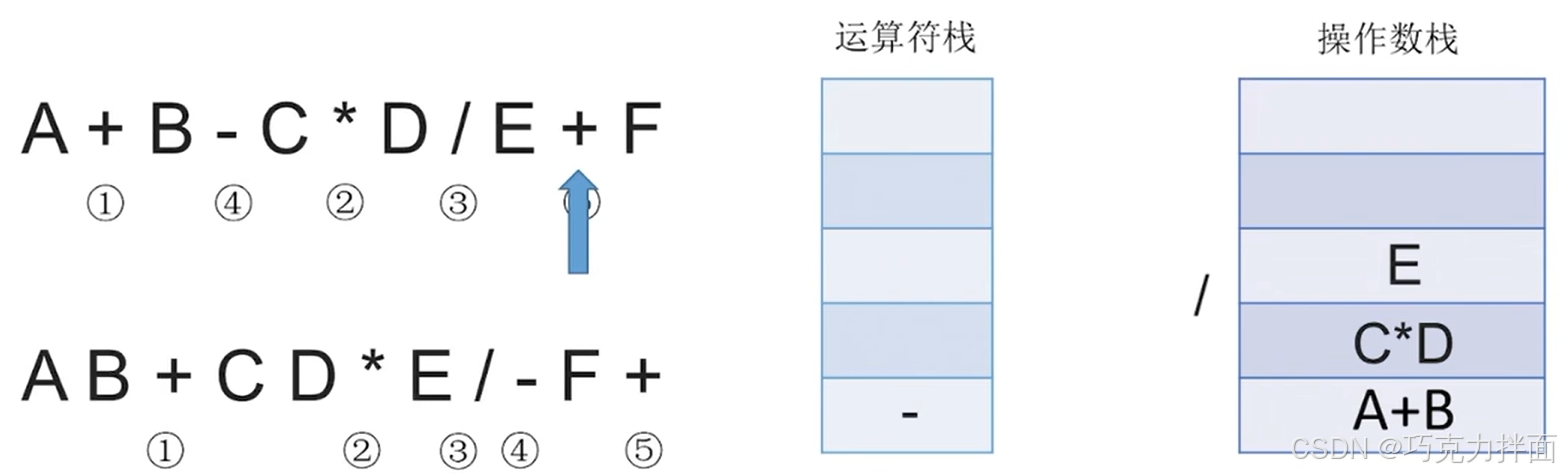
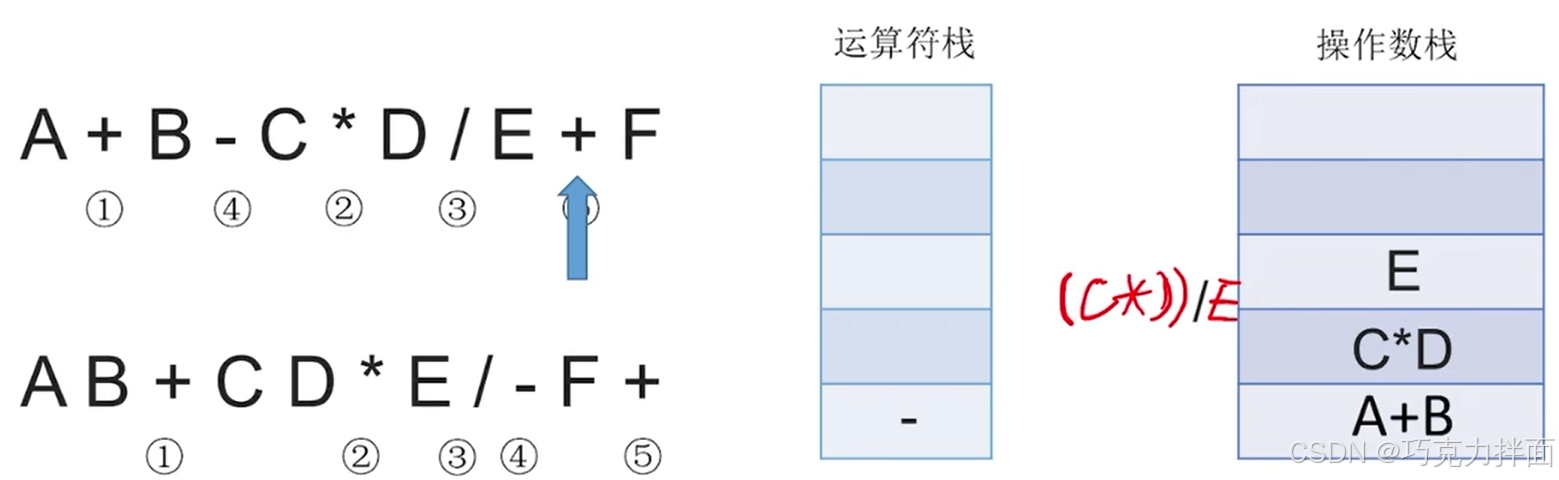
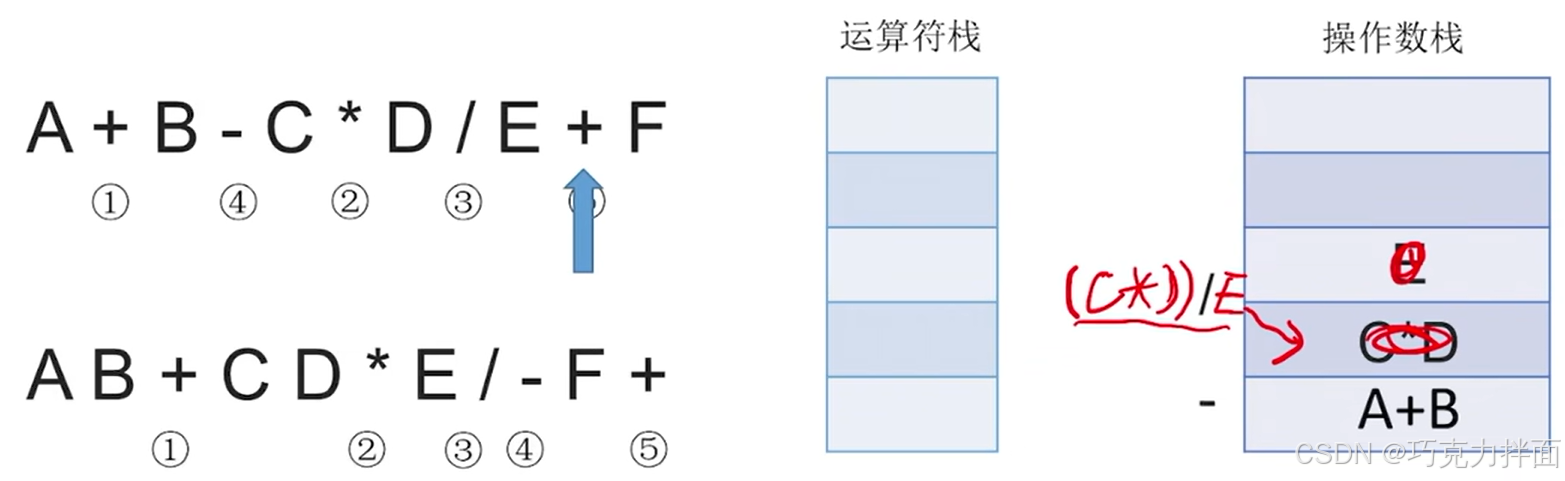
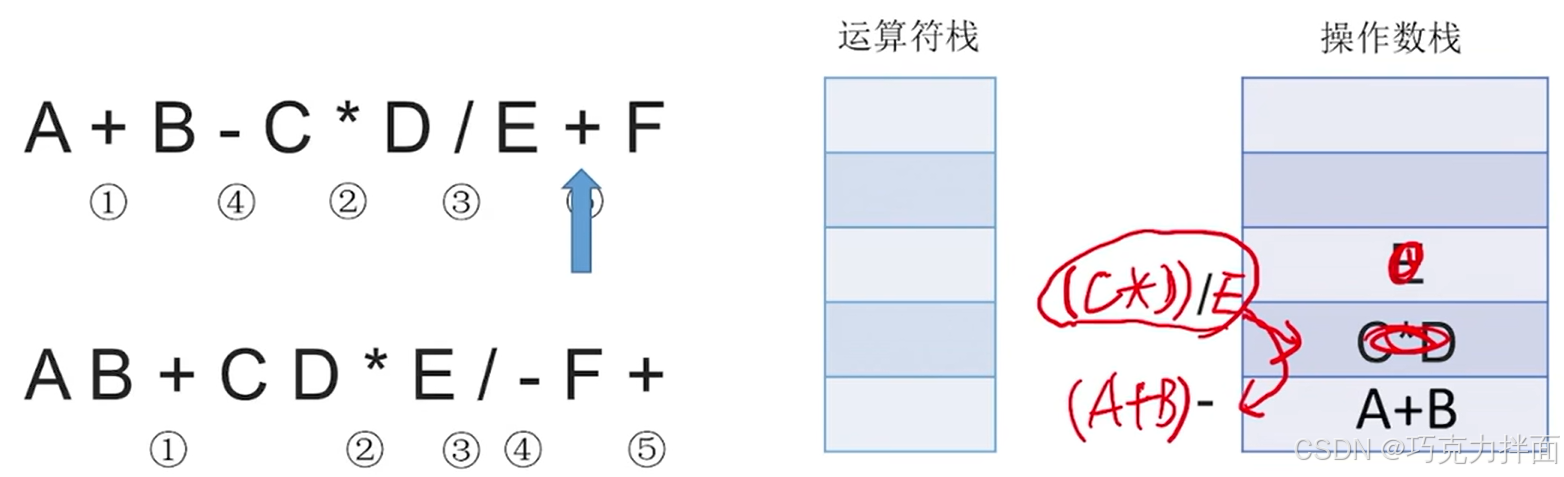
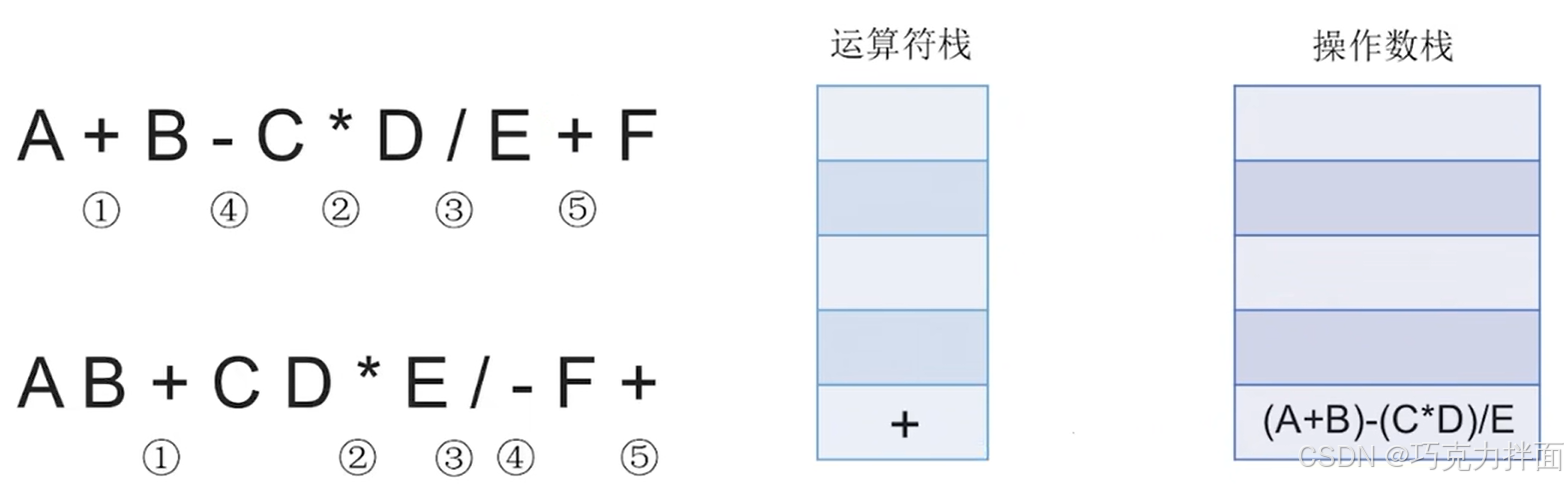
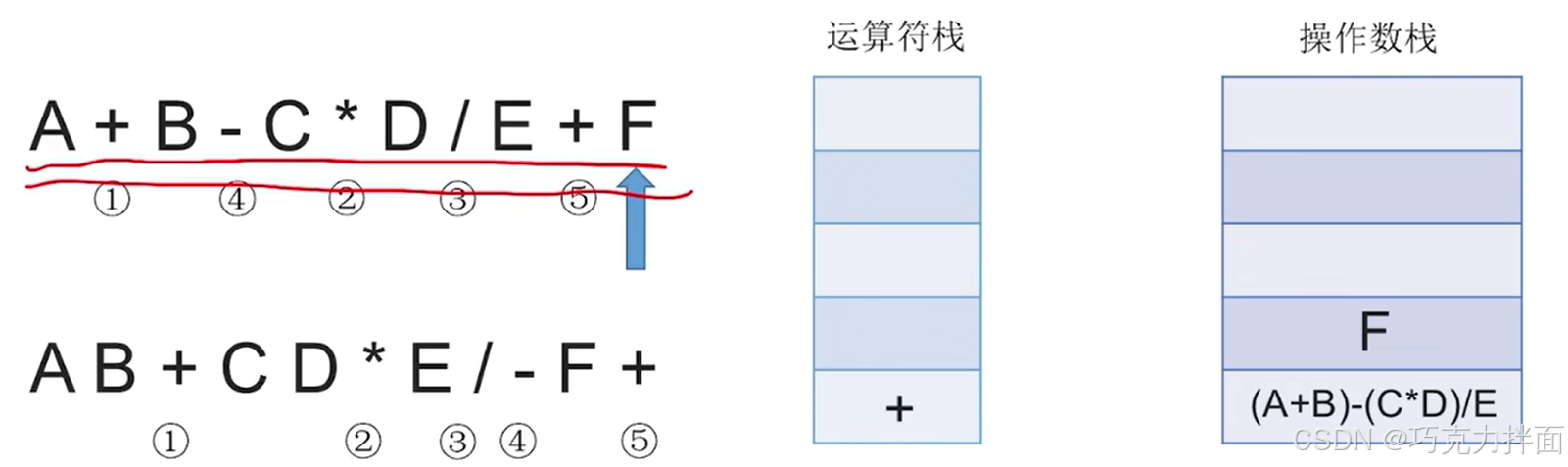
扫描到的第十一个数据为操作数F,因此压入操作数栈:
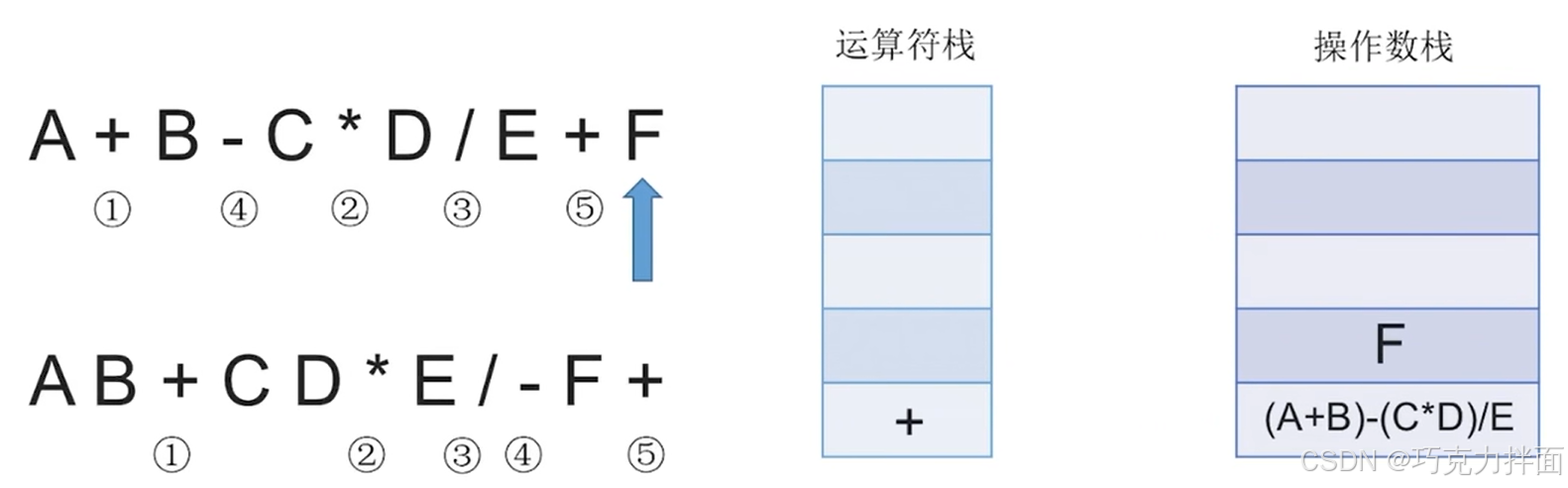
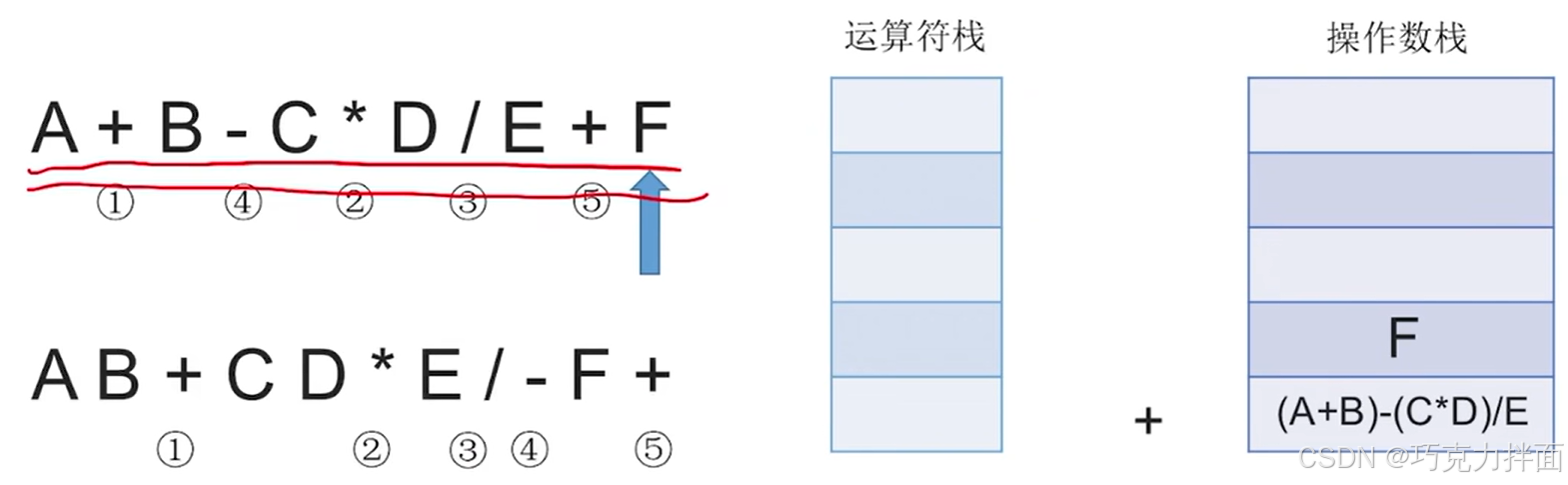
此时中缀表达式里的所有字符全部扫描完毕,根据"中缀表达式转后缀表达式"的规则,还需要把运算符栈里的所有运算符都依次弹出运算符栈,而且每弹出一个运算符就需要让该运算符生效即操作数栈里需要从操作数栈顶弹出两个元素,此时+弹出运算符栈,操作数栈就需要弹出F和(A+B)- (C * D)/E了,+生效的结果为((A+B)- (C * D)/E)+F,((A+B)- (C * D)/E)+F压入操作数栈顶,此时操作数栈里就没有F和(A+B)- (C * D)/E了,运算符栈全部处理完毕:
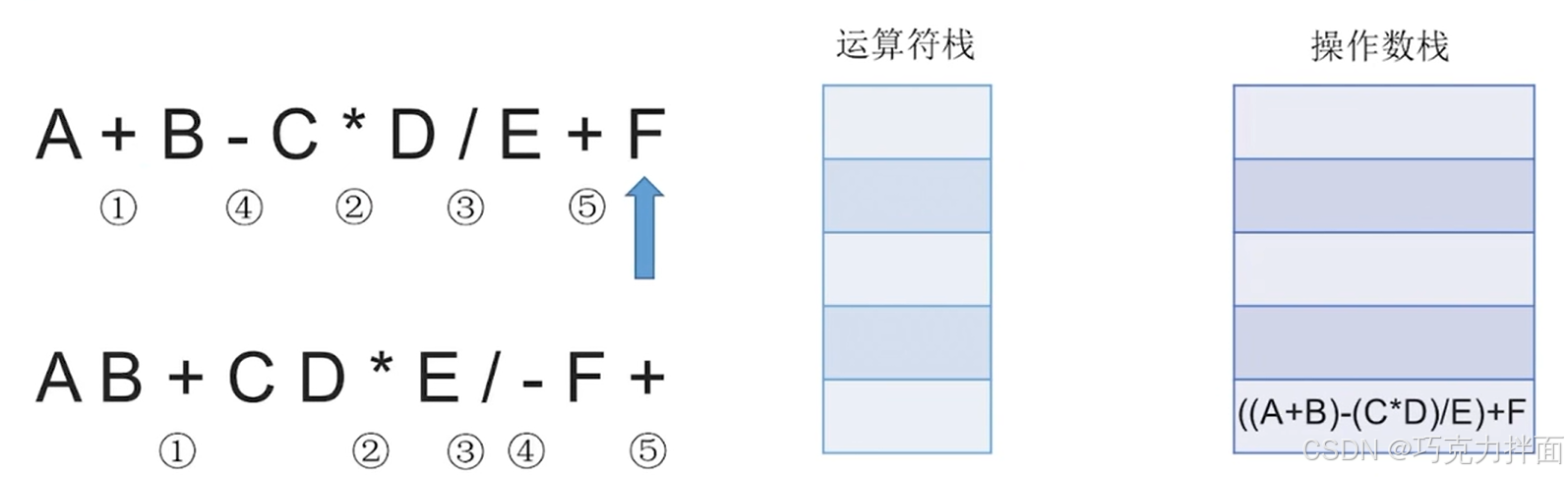
所以如果中缀表达式合法的话最终操作数栈里留下的结果就是中缀表达式的值。
2.心得:

中缀表达式计算的算法解法并不难,之所以将其复杂化,是因为中缀表达式计算的算法思路是把中缀表达式转后缀表达式和后缀表达式的计算相结合,这样的思想在计算机领域中是十分重要的,就是把中缀表达式计算的算法思路拆解为把中缀表达式转后缀表达式和后缀表达式的计算两个算法。
九.总结:























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








