深入理解HashMap

1、存储结构

• 数组

一段连续的存储单元来存储数据

• 哈希表（也叫散列表）

哈希（散列）函数 + 数组（散列表）

哈希函数：计算码值定位数组下标

数组：存储数据

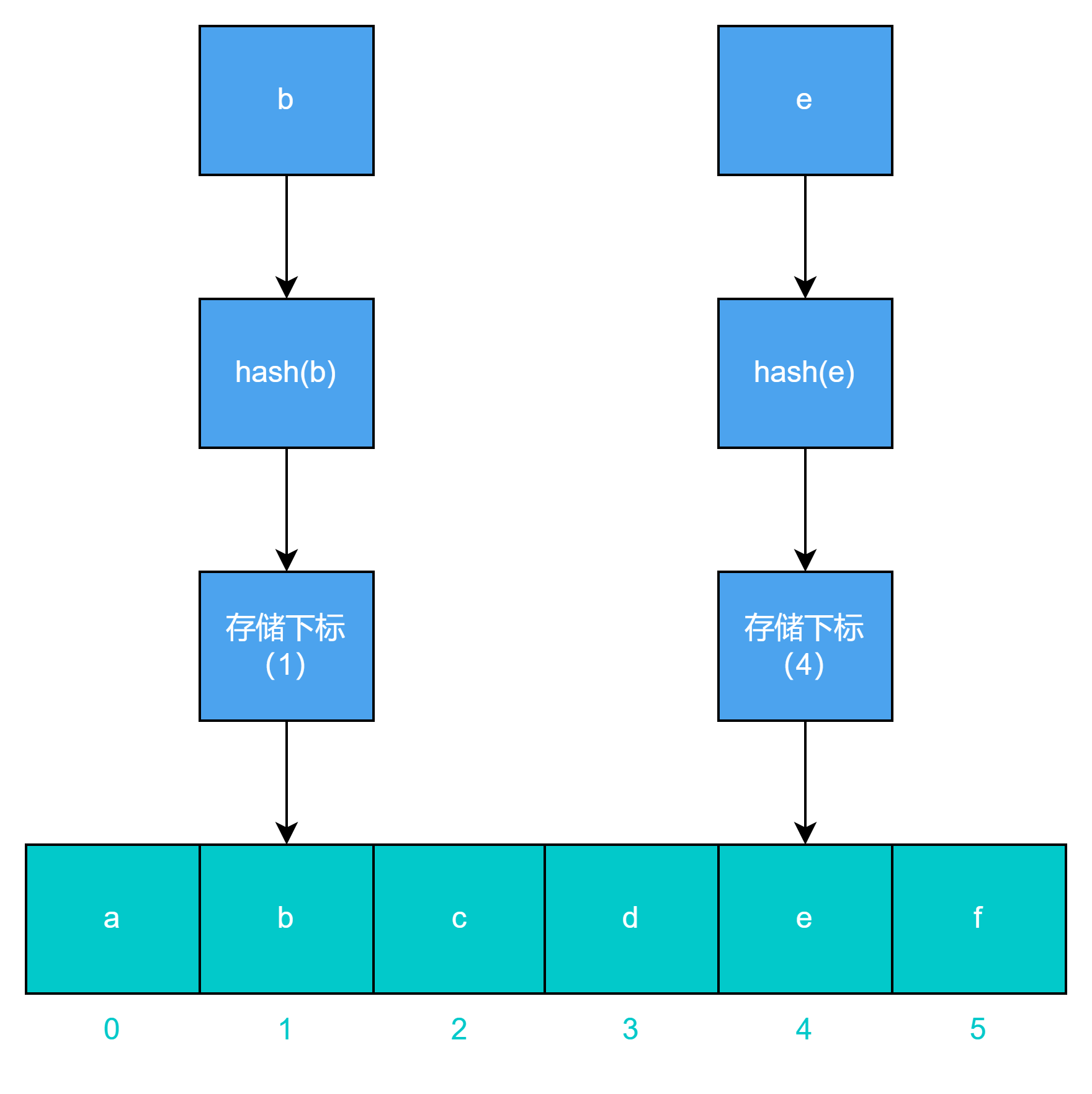
• 链表

非连续、非顺序的存储结构

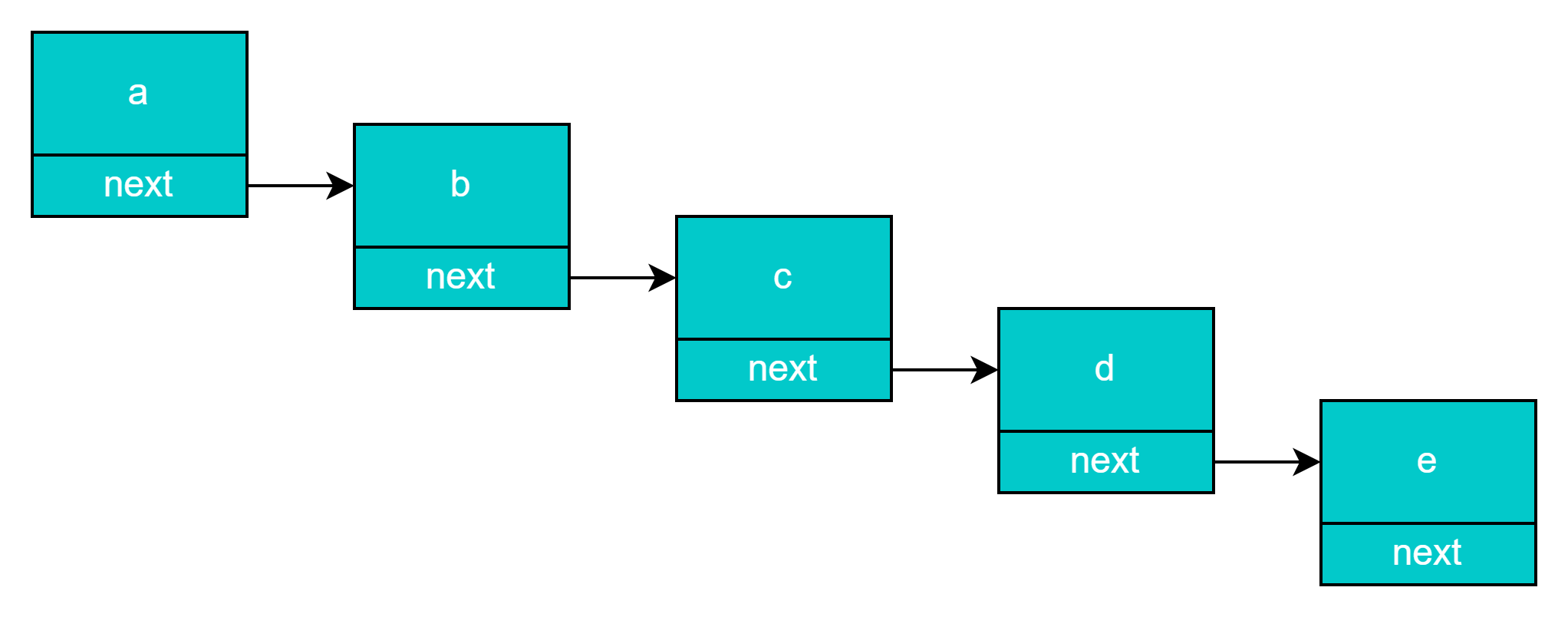
• 红黑树

（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

2、HashMap存储结构

哈希表（数组） + 链表 + 红黑树（链表长度 >= 8时）

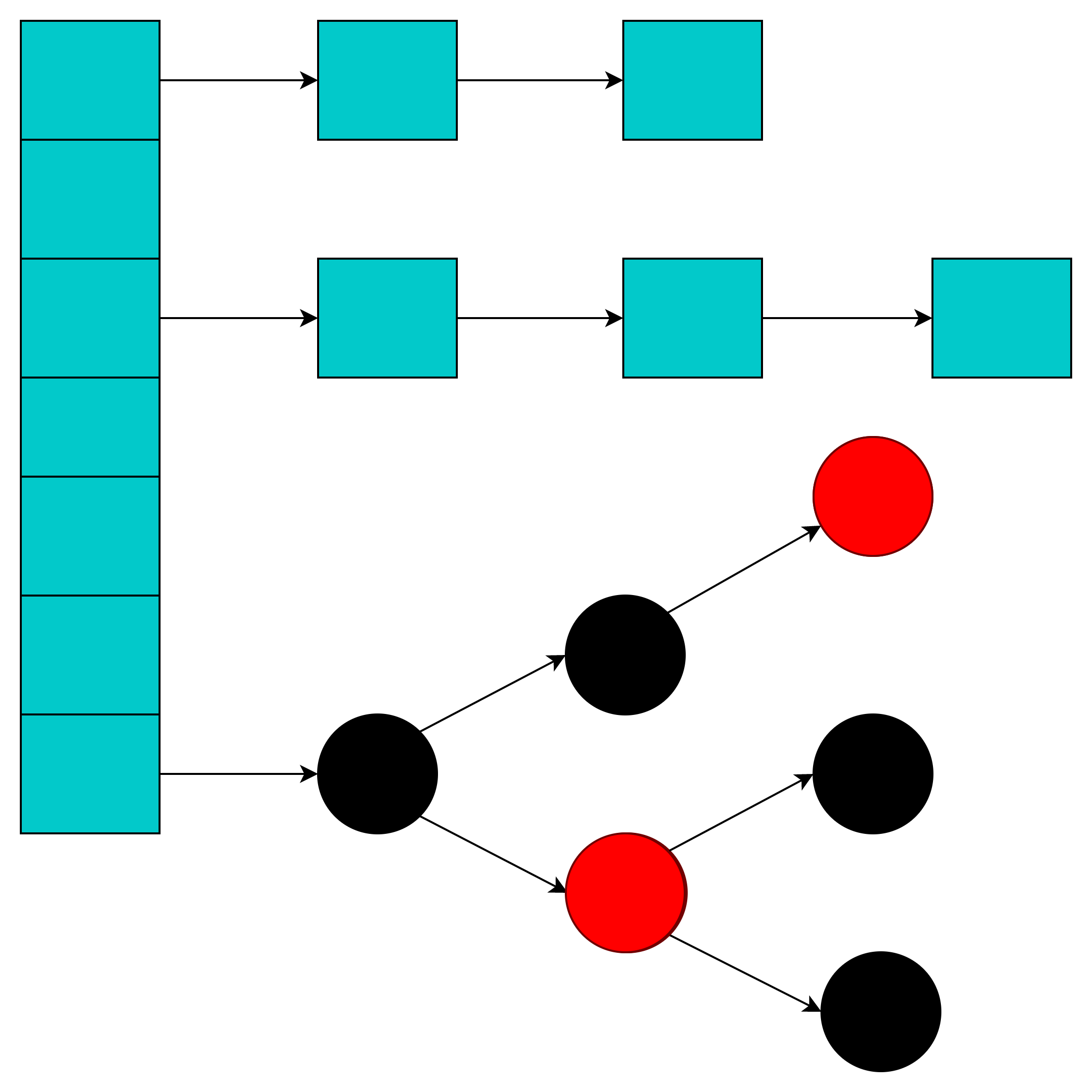
问题

1、为什么使用链表

通过Hash函数计算数组下标，但是Hash函数不是完美的，两个不同的元素，通过哈希函数得出的数组下标相同，这就是所谓的哈希冲突，也叫哈希碰撞。

HashMap采用链地址法，也就是数组 + 链表的方式，解决哈希冲突。

a元素通过hashCode函数计算下标为2，放入

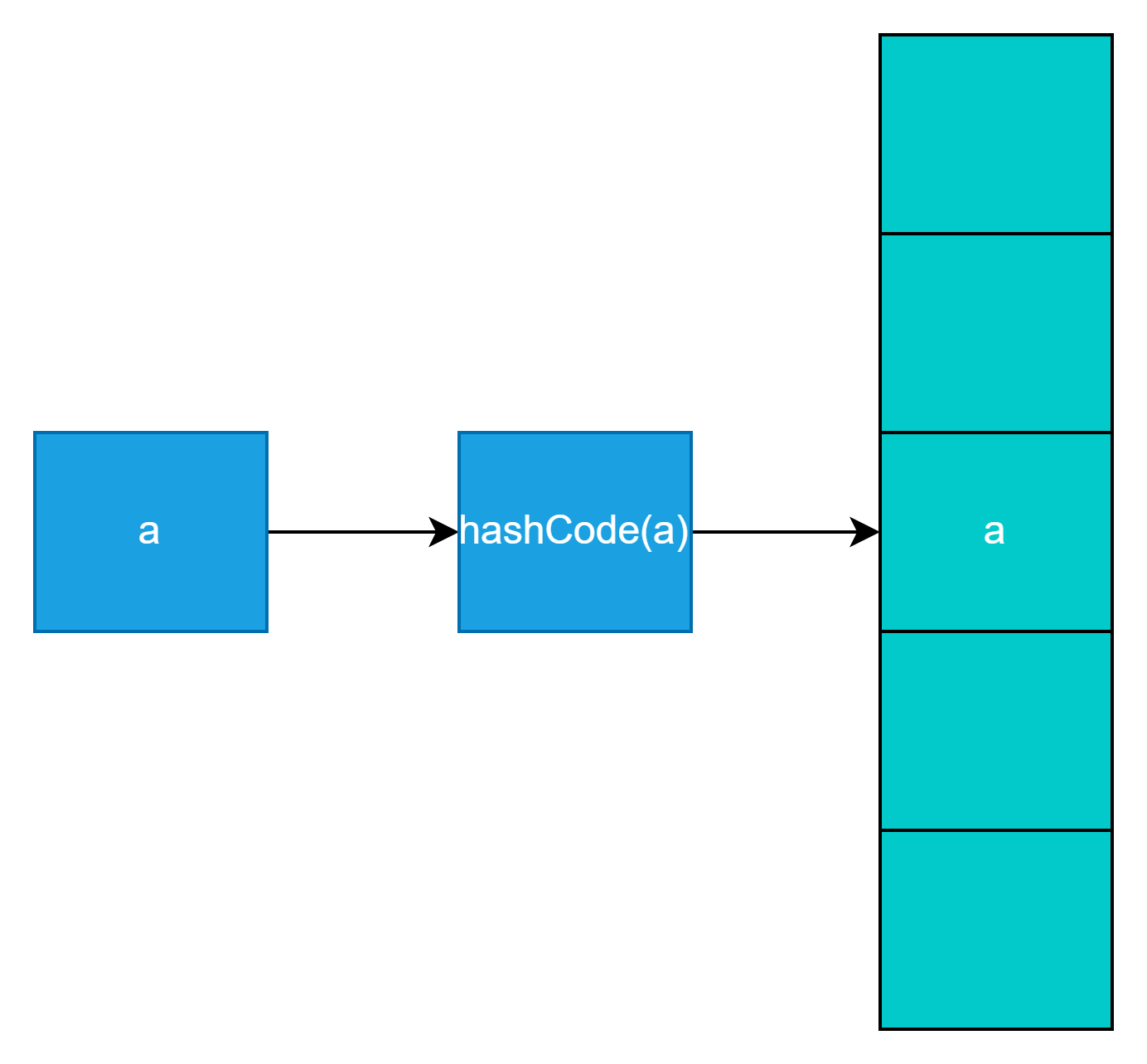
假设f元素通过hashCode函数计算下标也为2，放入时2位置已经存在元素，以链表方式放在2后位置

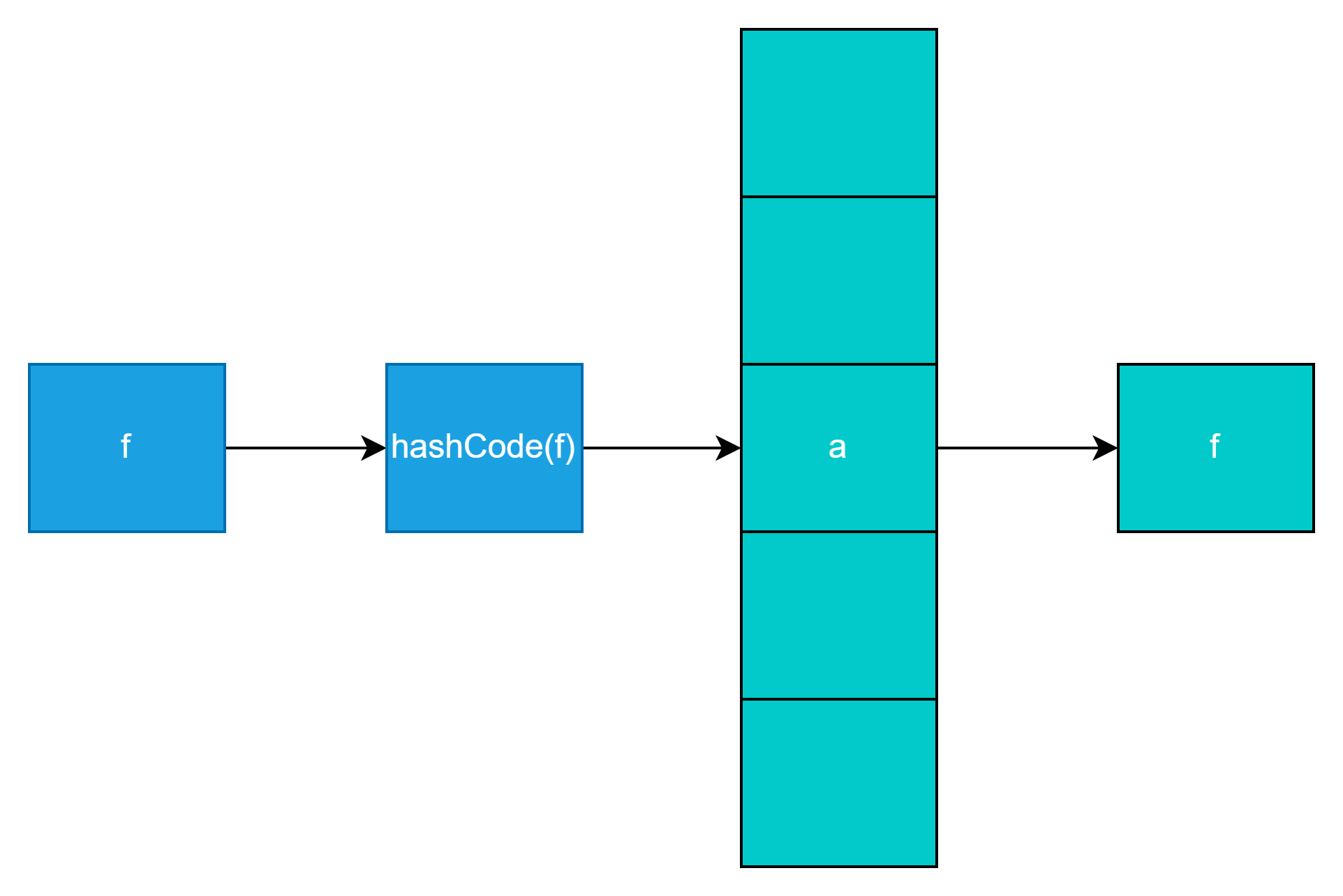
2、使用链表后如何定位元素

hashCode方法定位数组下标，equal方法比较元素内容一致。

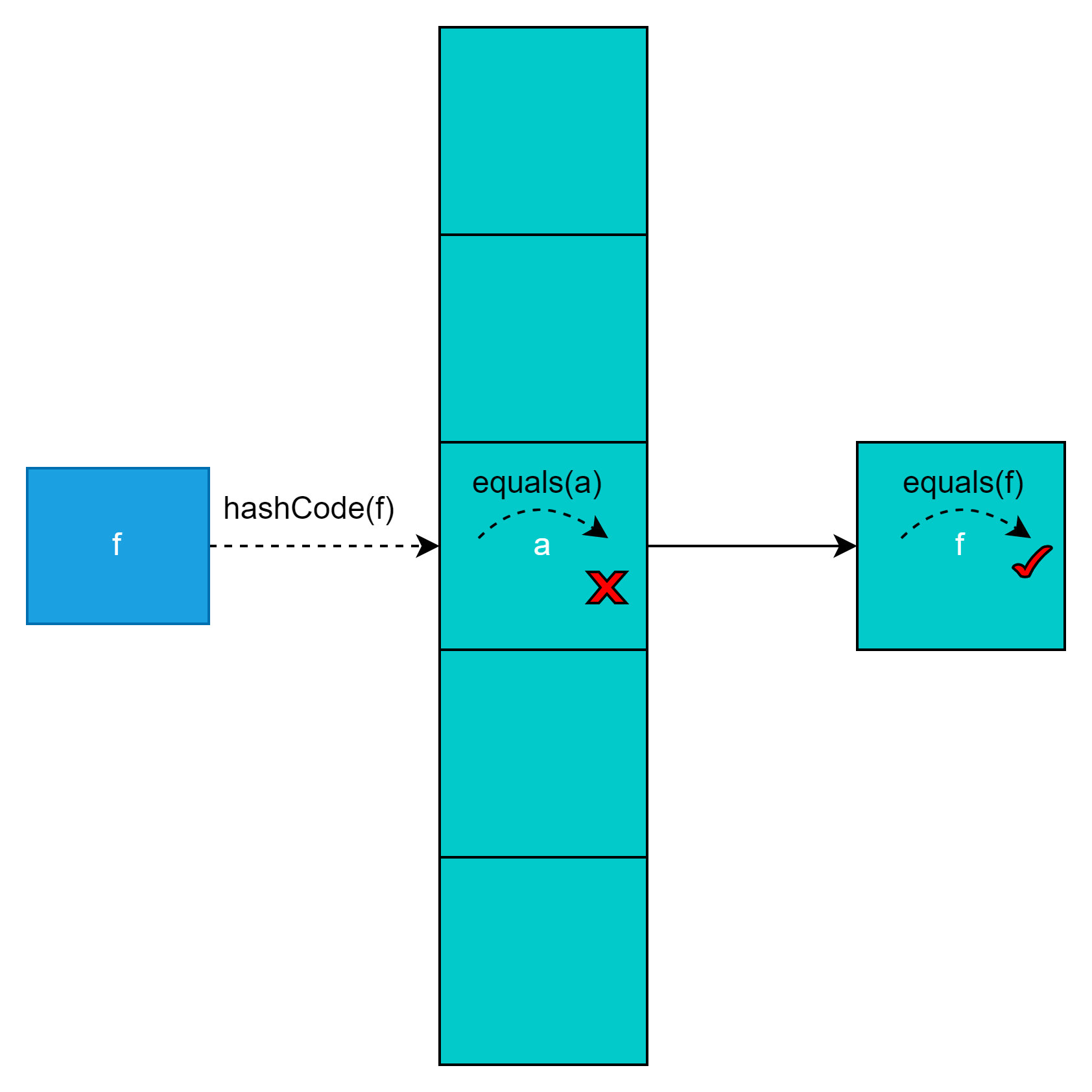
3、hashCode和equals

不同元素hashCode可以相同，所以hashCode相同，equals不一定相同 。

equals相同，说明在同一位置，所以hashCode一定相同。

4、有链表之后为什么需要红黑树？

如果元素的hashCode函数不是很好，链表上元素较多，查找效率非常低。

如图查找w元素，需要执行7次equals方法。

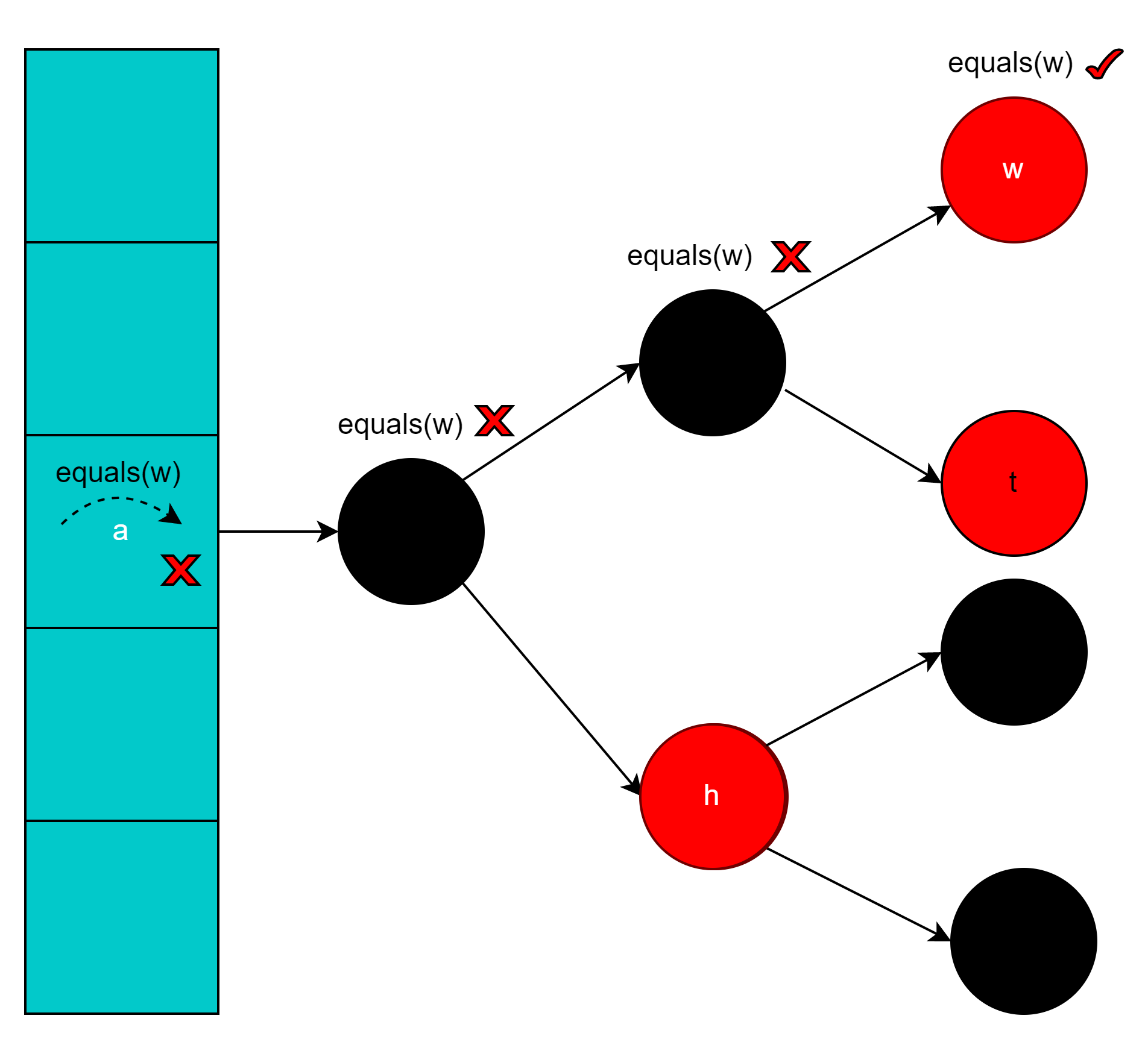
使用红黑树方式查找次数变少。

5、为什么不适用平衡二叉树，而使用红黑树。

二叉查找树的特点：

左子树的节点值比父亲节点小，而右子树的节点值比父亲节点大

二分查找的思想，快速找到某个节点。n 个节点的二叉查找树，正常的情况下，查找的时间复杂度为 O（logn）。

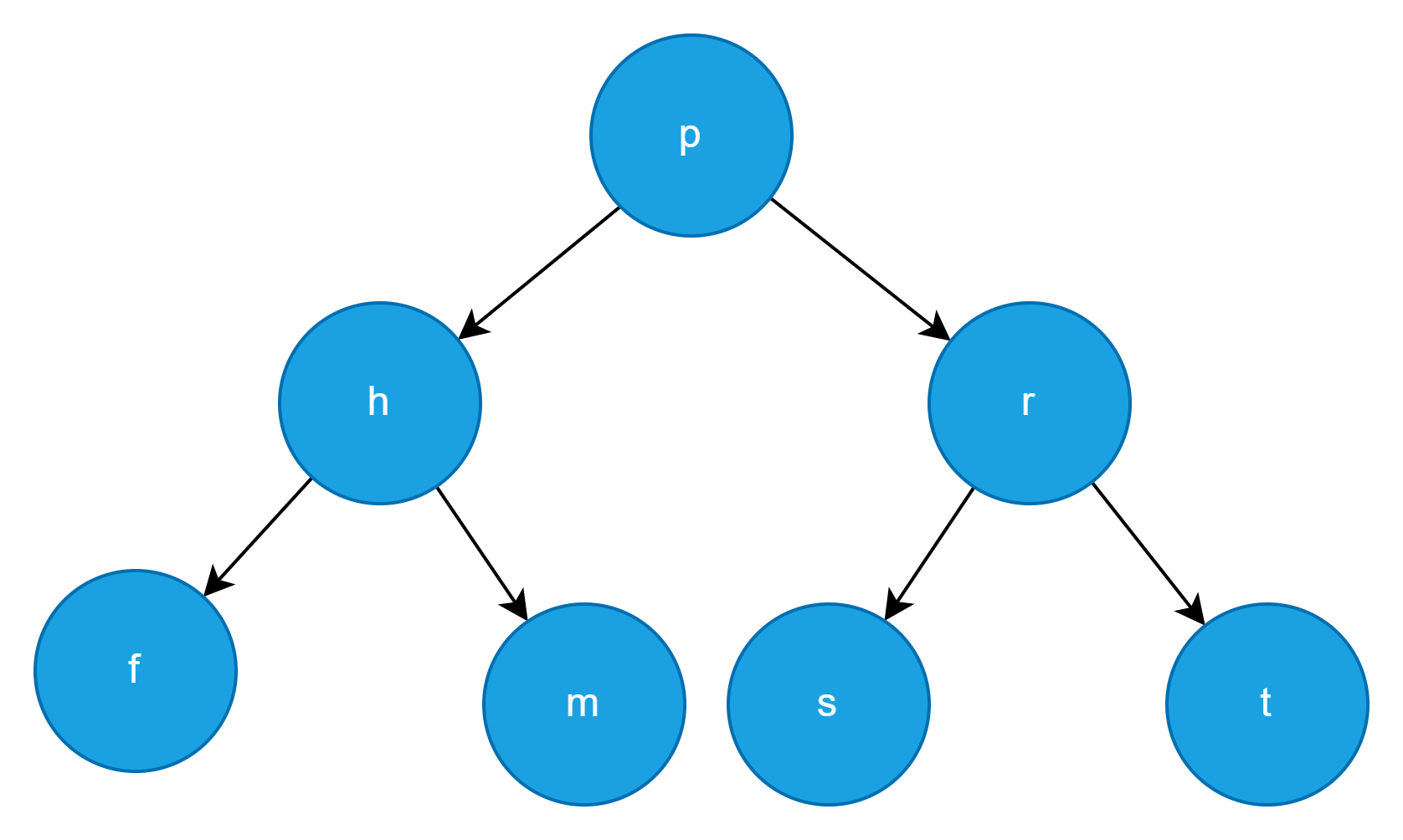
如果节点正好由从大到小的顺序插入，此时的二叉查找树已经近似退化为一条链表，这样的二叉查找树的查找时间复杂度顿时变成了 O(n)。

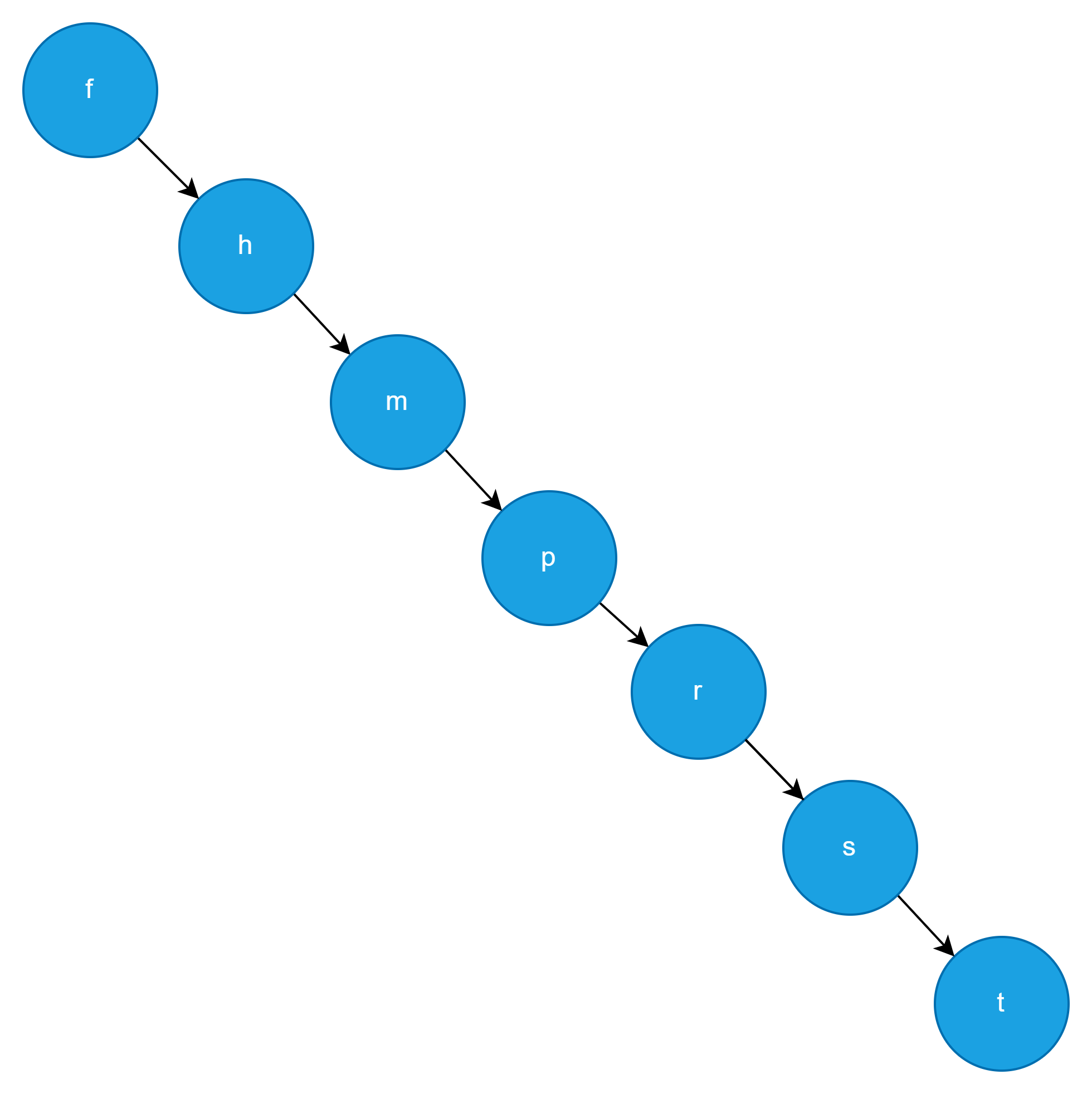
为了解决二叉排序树退化为链表的情况，引入了平衡二叉树。

平衡二叉树的特点有：

1、父节点最多拥有两个子节点；

2、父节点值大于左边子节点、小于右边子节点；

3、树的左右两边的层级数相差不会大于1；