最大比例

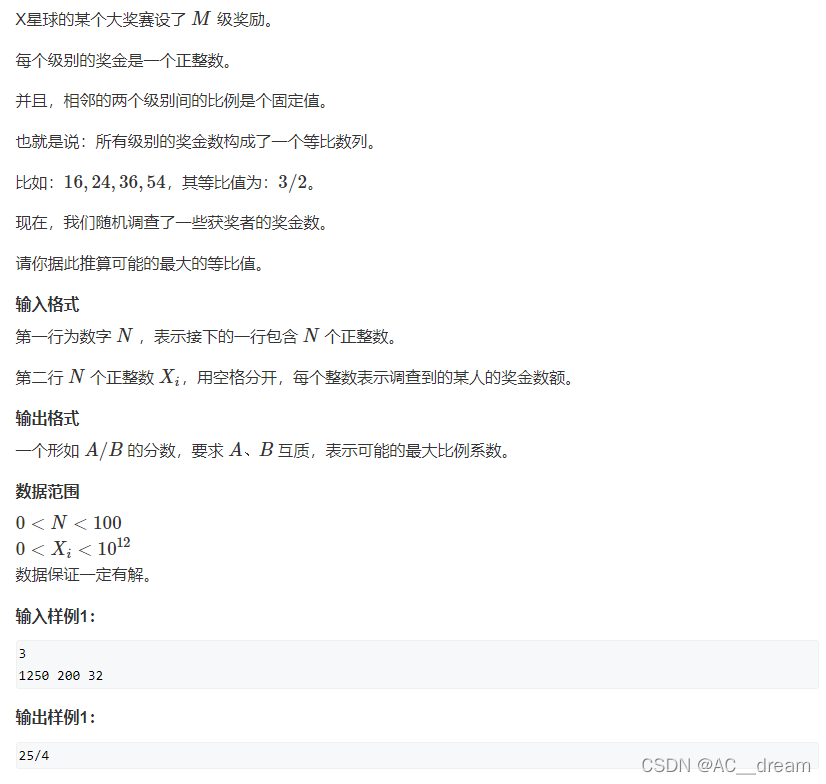
分析：为了保证所得的公比最大，首先要对原序列进行排序和去重，这个我就不细说了，我主要来说一下公比应该怎样求：

假设我们排完序的序列为a1,a2,……,an

那么我们可以对应的求出两两之间的比值为qi/pi，现在我们就是要求得p和q使得对于任意的两两相邻数的比值qi/pi为q/p的若干次方，而且为了使q/p尽量大，所以我们要保证若干次方尽可能小，那显然结果就是所有指数的最大公约数为1了，而且题目中保证有解，所以我们可以单独求分子和分母，最后算的次方肯定是一一对应的，现在的问题就转化为了如何求得p^x1,p^x2,……p^xn的最大满足p^x形式的公约数，其实写到这我们也不难发现，只需要求x1，x2，……xn之间的最大公约数即可得到x，但问题是xi在指数上，没法直接用求最大公约数的方法来进行求解，下面就需要介绍相减法来求得最大公约数。

先来看一下原始求得最大公约数的方法，若x>y>0,就返回gcd(y,x%y)，但是我们知道其实也可以返回gcd(y,x-y),只是这样进行比较慢而已，而这道题由于x在指数上，所以只能采取这种方法，我们可以利用两数相除来得到指数相减的目的，这样我们就可以求得满足要求形式的最大公约数，下面是相减法求最大公约数的代码：

ll gcd_sub(ll x,ll y)
{
	if(x<y) return gcd_sub(y,x);
	if(y==1) return x;
	return gcd_sub(y,x/y);
}

但是需要注意，相减法求最大公约数时本质上是用两数相除递归到下一次调用函数，所以终止条件应该是有一个数等于1.

下面是代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cmath>
using namespace std;
const int N=103;
typedef long long ll;
ll a[N],p[N],q[N];
ll gcd(ll x,ll y)
{
	if(y==0) return x;
	return gcd(y,x%y);
}
ll gcd_sub(ll x,ll y)
{
	if(x<y) return gcd_sub(y,x);
	if(y==1) return x;
	return gcd_sub(y,x/y);
}
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
		scanf("%lld",&a[i]);
	sort(a+1,a+n+1);
	int cnt=0;
	for(int i=2;i<=n;i++)
	{
		if(a[i]==a[i-1]) continue;
		else
		{
			ll t=gcd(a[i-1],a[i]);
			p[++cnt]=a[i-1]/t;
			q[cnt]=a[i]/t;
		}
	}
	ll ansp=p[1],ansq=q[1];
	for(int i=2;i<=cnt;i++)
	{
		ansp=gcd_sub(ansp,p[i]);
		ansq=gcd_sub(ansq,q[i]);
	}
	printf("%lld/%lld\n",ansq,ansp);
	return 0;
}