Average distance（树形dp）

昨天训练时遇到一道树形dp的题目，今天来给大家分享一下。

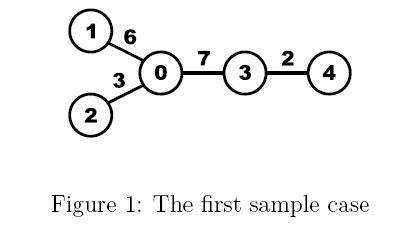
Given a tree, calculate the average distance between two vertices in the tree. For example, the average distance between two vertices in the following tree is (d01 + d02 + d03 + d04 + d12 +d13 +d14 +d23 +d24 +d34)/10 = (6+3+7+9+9+13+15+10+12+2)/10 = 8.6.

Input

On the first line an integer t (1 <= t <= 100): the number of test cases. Then for each test case:

One line with an integer n (2 <= n <= 10 000): the number of nodes in the tree. The nodes are numbered from 0 to n - 1.

n - 1 lines, each with three integers a (0 <= a < n), b (0 <= b < n) and d (1 <= d <= 1 000). There is an edge between the nodes with numbers a and b of length d. The resulting graph will be a tree.
 

Output

For each testcase:

One line with the average distance between two vertices. This value should have either an absolute or a relative error of at most 10-6
 

Sample Input

1
5
0 1 6
0 2 3
0 3 7
3 4 2

Sample Output

8.6

简单说一下题意，就是给你一棵树，然后你需要计算出两个顶点之间的平均距离，平均距离就是任意两个顶点之间的距离和除以对应的通路数，看题目中的例子即可

在上个博客中我介绍了树的两种遍历更新方式，我们就先来用这种方法做一下，我们需要先记录一下以每个节点为根的子树中节点的个数，我们令dp[x][1]表示以x为根的子树中的所有点到x的距离和，我们令dp[x][2]表示图中所有点到x的距离和，如果对这两个数组的求法还不是很了解的话可以看我上次的博客（常见树形dp递归更新方法），下面直接给出代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=30003;
ll h[N],ne[N],e[N],w[N],idx;
ll dp[N][2];
ll cnt[N];
int n;
void add(int x,int y,int z)
{
	e[idx]=y;
	w[idx]=z;
	ne[idx]=h[x];
	h[x]=idx++;
}
void dfs1(int x,int father)
{
	cnt[x]=1;
	for(int i=h[x];i!=-1;i=ne[i])
	{
		int j=e[i];
		if(j==father) continue;
		dfs1(j,x);
		cnt[x]+=cnt[j];//递归求出以x为根的子树中节点的个数 
		dp[x][1]+=dp[j][1]+cnt[j]*w[i];//求出以x为根的子树中的节点到x的距离和 
	}
}
void dfs2(int x,int father)
{
	for(int i=h[x];i!=-1;i=ne[i])
	{
		int j=e[i];
		if(j==father) continue;
		dp[j][2]=dp[x][2]+(n-2*cnt[j])*w[i];//递归求出树中全部的点到j的距离和 
		dfs2(j,x);
	}
}
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		scanf("%d",&n);
		int u,v,l;
		memset(h,-1,sizeof h);
		idx=0;
		for(int i=1;i<n;i++)
		{
			scanf("%d%d%d",&u,&v,&l);
			add(u,v,l);add(v,u,l);
		}
		memset(cnt,0,sizeof cnt);
		memset(dp,0,sizeof dp);
		dfs1(0,0);
		dp[0][2]=dp[0][1];//以根节点为根的子树就是整棵树，如果忘记赋值就会出错 
		dfs2(0,0);
		long long ans=0;
		for(int i=0;i<n;i++)
			ans+=dp[i][2];
		printf("%.10lf\n",(double)ans/n/(n-1));
	}
	return 0;
}

下面我再给出一种用边的贡献来解决本道题的思路

以题目中给的样例图为例，我们考虑0号点与3号点之间的边，我们计算任意两点之间的距离时，这条边一共被计算了多少次呢？换句话说两点之间的距离包含这条边时，这两个点具有什么关系呢？是不是这两个点分别在这条边的两端？也就是1，2，0三个点其中之一与3，4两个点其中之一的距离中才会包括这条边？所以我们只需要记录以每个点为根的子树中的节点个数即可，最后对（n-cnt[i]）*cnt[i]*w取一个和即可，下面是代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
using namespace std;
typedef long long ll;
const int N=30000;
int h[N],e[N],w[N],ne[N],idx;
ll dp[N],cnt[N];
//dp[i]记录以i为根的子树中的边的边权贡献之和 
int n;
void add(int x,int y,int z)
{
	e[idx]=y;
	w[idx]=z;
	ne[idx]=h[x];
	h[x]=idx++;
}
void dfs(int x,int father)
{
	cnt[x]=1;
	for(int i=h[x];i!=-1;i=ne[i])
	{
		int j=e[i];
		if(j==father) continue;
		dfs(j,x);
		cnt[x]+=cnt[j];
		dp[x]+=dp[j]+cnt[j]*(n-cnt[j])*w[i];
	}
}
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		memset(h,-1,sizeof h);
		idx=0;
		scanf("%d",&n);
		int u,v,z;
		for(int i=1;i<n;i++)
		{
			scanf("%d%d%d",&u,&v,&z);
			add(u,v,z);add(v,u,z); 
		}
		dfs(0,0);
		printf("%.10lf\n",(double)dp[0]/n/(n-1)*2);
	}
	return 0;
}

这道题目给了我一种计算满足某种和关系的全新方法，就是利用边的贡献来解决，由于这种方法我用的比较少，所以现在还没办法做出系统的总结，欢迎大佬补充！