HDU 4565 So Easy!

最新推荐文章于 2020-03-05 15:29:58 发布

原创最新推荐文章于 2020-03-05 15:29:58 发布 · 1k 阅读

0 ·

CC 4.0 BY-SA版权

HDU 专栏收录该内容

32 篇文章

订阅专栏

So Easy!

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 803 Accepted Submission(s): 219

Problem Description

　　A sequence S _n is defined as:

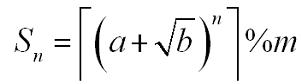
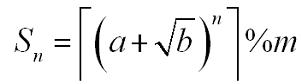
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S _n.
　　You, a top coder, say: So easy!

Input

　　There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2 ¹⁵, (a-1) ²< b < a ², 0 < b, n < 2 ³¹.The input will finish with the end of file.

Output

　　For each the case, output an integer S _n.

Sample Input

Sample Output

Source

2013 ACM-ICPC长沙赛区全国邀请赛——题目重现

Recommend

zhoujiaqi2010
第一次做与矩阵的题目，将题目化简后就是求矩阵的快速幂

#include <iostream>
#include <cstring>
#include <cstdio>
#define N 3
using namespace std;
__int64 rec1[N][N],rec2[N][N],temp[N][N];
__int64 a,b,n,mod;
int main()
{
    //freopen("data.in","r",stdin);
    void get(int k);
    while(scanf("%I64d %I64d %I64d %I64d",&a,&b,&n,&mod)!=EOF)
    {
        if(n==1)
        {
            printf("%I64d\n",2*a%mod);
            continue;
        }
        rec1[1][1] = 2*a; rec1[1][2] =(b-a*a);
        rec1[2][1] = 1; rec1[2][2] = 0;
        get(n-1);
        printf("%I64d\n",((rec2[1][1]*2*a)%mod+(rec2[1][2]*2)%mod)%mod);
    }
    return 0;
}
void get_rec(__int64 (*p1)[3],__int64 (*p2)[3])
{
    memset(temp,0,sizeof(temp));
    for(int i=1;i<=2;i++)
    {
        for(int j=1;j<=2;j++)
        {
            for(int x=1;x<=2;x++)
            {
                temp[i][j] += (p1[i][x]%mod*p2[x][j]%mod);
                temp[i][j] = (temp[i][j])%mod;
            }
        }
    }
    for(int i=1;i<=2;i++)
    {
        for(int j=1;j<=2;j++)
        {
            p2[i][j] = (temp[i][j]+mod)%mod;
        }
    }
}
void get(int k)
{
    rec2[1][1] =1; rec2[1][2] = 0;
    rec2[2][1] =0; rec2[2][2] = 1;
    while(k>1)
    {
        if(k&1)
        {
            get_rec(rec1,rec2);
        }
        get_rec(rec1,rec1);
        k = k/2;
    }
    get_rec(rec1,rec2);
}