POJ 1765 November Rain

最新推荐文章于 2017-11-30 15:51:47 发布

原创最新推荐文章于 2017-11-30 15:51:47 发布 · 3k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#线段树

POJ 专栏收录该内容

182 篇文章

订阅专栏

November Rain

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 2097		Accepted: 448
Case Time Limit: 2000MS

Description

Contemporary buildings can have very complicated roofs. If we take a vertical section of such a roof it results in a number of sloping segments. When it is raining the drops are falling down on the roof straight from the sky above. Some segments are completely exposed to the rain but there may be some segments partially or even completely shielded by other segments. All the water falling onto a segment as a stream straight down from the lower end of the segment on the ground or possibly onto some other segment. In particular, if a stream of water is falling on an end of a segment then we consider it to be collected by this segment.

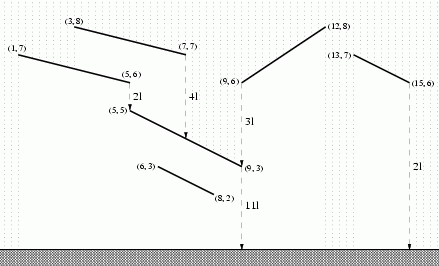
For the purpose of designing a piping system it is desired to compute how much water is down from each segment of the roof. To be prepared for a heavy November rain you should count one liter of rain water falling on a meter of the horizontal plane during one second.

Task
Write a program that:

reads the description of a roof,
computes the amount of water down in one second from each segment of the roof,
writes the results.

Input

The first line of the input contains one integer n (1 <= n < = 40000) being the number of segments of the roof. Each of the next n lines describes one segment of the roof and contains four integers x1, y1, x2, y2 (0 <= x1, y1, x2, y2 < = 1000000, x1 < x2, y1<>y2) separated by single spaces. Integers x1, y1 are respectively the horizontal position and the height of the left end of the segment. Integers x2, y2 are respectively the horizontal position and the height of the right end of the segment. The segments don't have common points and there are no horizontal segments. You can also assume that there are at most 25 segments placed above any point on the ground level.

Output

The output consists of n lines. The i-th line should contain the amount of water (in liters) down from the i-th segment of the roof in one second.

Sample Input

Sample Output

Source

Central Europe 2003

线段树好题，花了很长的时间的构思，首先这道题离散化是肯定的。建立了两棵线段树，一是段更新，来维护遮蔽的区间。二是点更新，来维护从某一点下来的水量。

查了很长时间的代码，没想到却死在了sort上，在排序的时候数据超出int了导致溢出了，小遗憾啊

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cmath>
#include <map>
#define N 41000
using namespace std;
struct num
{
    int l,r,tl,tr;
    __int64 sum;
}a[8*N],b[8*N];
struct Num
{
    __int64 x1,y1,x2,y2;
    int pos;
}c[N];
int x[2*N];
__int64 ans[N];
map<int,int>ma,ma1;
int w = 0;
bool cmp(Num p1,Num p2)
{
    if(p2.x1>=p1.x1&&p2.x1<=p1.x2)
    {
        double y = (double)((p1.y2-p1.y1)*(p2.x1-p1.x1))/(p1.x2-p1.x1) + (double)p1.y1;
        return y>(double)p2.y1;
    }
    if(p2.x2>=p1.x1&&p2.x2<=p1.x2)
    {
        double y = (double)((p1.y2-p1.y1)*(p2.x2-p1.x1))/(p1.x2-p1.x1) + (double)p1.y1;
        return y>(double)p2.y2;
    }
    int k1 = min(p1.y1,p1.y2);
    int k2 = min(p2.y1,p2.y2);
    if(k1!=k2)
    {
        return k1>k2;
    }else
    {
        return p1.x2<p2.x1;
    }
}
int main()
{
    //freopen("data.txt","r",stdin);
    void build1(int k,int l,int r);
    void build2(int k,int l,int r);
    __int64 find1(int k,int l,int r);
    __int64 find2(int k,int l,int r);
    void update2(int k,int l,int val);
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=1;i<=n;i++)
        {
            scanf("%I64d %I64d %I64d %I64d",&c[i].x1,&c[i].y1,&c[i].x2,&c[i].y2);
            c[i].pos = i;
            x[2*i-1] = c[i].x1;
            x[2*i] = c[i].x2;
        }
        sort(c+1,c+n+1,cmp);
        sort(x+1,x+2*n+1);
        int Top = 0;
        ma.clear();
        ma1.clear();
        for(int i=1;i<=2*n;i++)
        {
            int k = x[i];
            if(ma[k]==0)
            {
                ma[k]=++Top;
                ma1[Top] = k;
            }
        }
        build1(1,1,Top);
        build2(1,1,Top);
        for(int i=1;i<=n;i++)
        {
            __int64 res1 = find1(1,c[i].x1,c[i].x2);
            res1 = c[i].x2-c[i].x1-res1;
            __int64 res2 =find2(1,c[i].x1,c[i].x2);
            res1 = res1+res2;
            if(c[i].y1>c[i].y2)
            {
                update2(1,c[i].x2,res1);
            }else
            {
                update2(1,c[i].x1,res1);
            }
            ans[c[i].pos] = res1;
        }
        for(int i=1;i<=n;i++)
        {
            printf("%I64d\n",ans[i]);
        }
    }
    return 0;
}
void build1(int k,int l,int r)
{
    a[k].l = l; a[k].r = r;
    a[k].tl = ma1[l]; a[k].tr = ma1[r];
    a[k].sum = 0;
    if(l+1==r)
    {
        return ;
    }
    int mid = (l+r)>>1;
    build1(k<<1,l,mid);
    build1(k<<1|1,mid,r);
}
void pushup1(int k)
{
    a[k].sum = a[k<<1].sum+a[k<<1|1].sum;
}
__int64 find1(int k,int l,int r)
{
    if(a[k].tl==l&&a[k].tr==r)
    {
        __int64 val = a[k].sum;
        a[k].sum = r-l;
        return val;
    }
    if(a[k].tl<=l&&a[k].tr>=r&&(a[k].sum==a[k].tr-a[k].tl))
    {
        return r-l;
    }
    __int64 sum;
    if(a[k<<1].tr>=r)
    {
        sum = find1(k<<1,l,r);
    }else if(a[k<<1|1].tl<=l)
    {
        sum = find1(k<<1|1,l,r);
    }else
    {
        sum = find1(k<<1,l,a[k<<1].tr);
        sum += find1(k<<1|1,a[k<<1|1].tl,r);
    }
    pushup1(k);
    return sum;
}
void build2(int k,int l,int r)
{
    b[k].l = l; b[k].r = r;
    b[k].tl = ma1[l]; b[k].tr = ma1[r];
    b[k].sum = 0;
    if(l==r)
    {
        return ;
    }
    int mid = (l+r)>>1;
    build2(k<<1,l,mid);
    build2(k<<1|1,mid+1,r);
}
void pushup2(int k)
{
    b[k].sum = b[k<<1].sum+b[k<<1|1].sum;
}
__int64 find2(int k,int l,int r)
{
    if(b[k].tl==l&&b[k].tr==r)
    {
        __int64 val = b[k].sum;
        b[k].sum = 0;
        return val;
    }
    __int64 sum;
    if(b[k].sum==0)
    {
        b[k<<1].sum = 0;
        b[k<<1|1].sum = 0;
    }
    if(b[k<<1].tr>=r)
    {
        sum = find2(k<<1,l,r);
    }else if(b[k<<1|1].tl<=l)
    {
        sum = find2(k<<1|1,l,r);
    }else
    {
        sum = find2(k<<1,l,b[k<<1].tr);
        sum +=find2(k<<1|1,b[k<<1|1].tl,r);
    }
    pushup2(k);
    return sum;
}
void update2(int k,int l,int val)
{
    if(b[k].tl ==l&&b[k].tr==l)
    {
        b[k].sum+=val;
        return;
    }
    if(b[k].sum==0)
    {
        b[k<<1].sum = 0;
        b[k<<1|1].sum = 0;
    }
    if(b[k<<1].tr>=l)
    {
       update2(k<<1,l,val);
    }else if(b[k<<1|1].tl<=l)
    {
       update2(k<<1|1,l,val);
    }
    pushup2(k);
}