人工智能经典问题，八数码问题，UCS(等代价搜索），C语言版，保证看懂，分析到位，注释详细，没有bug

一、问题描述

1. 3*3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空。
2. 要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态（图左）到目标状态（图右）。

二、迟来的代码

// 备注：采用曼哈顿距离计算初始状态与当前状态的水平距离和垂直距离之和

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>

#define N 	3	// 阶数，可以改为更高阶

// 定义一个结构体来表示棋盘状态
typedef struct node
{
	int cost;			// 从初始状态到本状态的代价
    int data[N][N];		// 存放棋盘状态
	struct node *prev;	// 链表中的前指针
    struct node *next;	// 链表中的后指针
    struct node *father;// 搜索树的父节点
}node;

node *open;			// open表，存放未拓展的节点
node *close;		// close表，存放已经拓展的节点
static int n = 0;	// 用来记录总共搜索的次数

int src[N][N] = {2, 8, 3, 1, 0, 4, 7, 6, 5};	// 初始状态
int cur[N][N];	// 当前状态
int dest[N][N] = {1, 2, 3, 8, 0, 4, 7, 6, 5};	// 目标状态

// 生成一个节点
node *initList()
{
    int i, j;
	node *p = malloc(sizeof(node));

	if(!p)
	{
		printf("malloc fail\n");
		return NULL;
	}

    p->prev = p;
    p->next = p;
    p->father = NULL;
	p->cost = 0;
    
	// 初始化棋盘状态
    for(i = 0; i < N; i++)
    {
        for(j = 0; j < N; j++)
        {
            p->data[i][j] = -1;
        }
    }

	return p;
}

// 头插法，把节点插入到链表头部
void head_insert(node *head, node *p)
{
	p->next = head->next;
	p->prev = head;
	head->next->prev = p;
	head->next = p;
}

// 尾插法，把节点插入到链表尾部
void tail_insert(node *head, node *p)
{
	p->prev = head->prev;
	head->prev->next = p;
	p->next = head;
	head->prev = p;
}

// 弹出节点
void Remove(node *p)
{
	p->prev->next = p->next;
	p->next->prev = p->prev;
	p->next = p;
	p->prev = p;
}

// 清空链表
void clearList(node *head)
{
    // 空表不需要再清空
    if(!head || head->next == head)
    {
        printf("list is null\n");
        return;
    }

    // 头删法，跟头插法相似，循环删除首元节点
    for(node *p = head->next; p != head; p = head->next)
    {
        Remove(p);  // 弹出节点p
        free(p);    // 释放节点p的空间
    }
}

// 初始化棋盘
void init()
{
	int i, j, k;
	int a[N*N] = {1, 2, 3, 8, 0, 4, 7, 6, 5};
	int flag[N*N] = {0};	// 用来标记0~8中哪个数字已经出现过

	srand(time(0));
	
 	for(i = 0; i < N; i++)
	{
		for(j = 0; j < N; j++)
		{
			// 尝试生成一个0~8间的数字
			k = rand()%(N*N);
			while(1)
			{
				// 如果该数字未出现
				if(flag[k] == 0)	
				{
					flag[k] = 1;	// 修改标志位
					src[i][j] = a[k]; // 初始化对应src的位置
					break;
				}
				// 重新生成数字
				k = rand()%(N*N);
			}
		}	
	}
}

// 复制棋盘状态
void copy(int source[N][N], int dest1[N][N])
{
	int i, j;
	for(i = 0; i < N; i++)
	{
		for(j = 0; j < N; j++)
		{
			dest1[i][j] = source[i][j];
		}
	}
}

// 打印棋盘状态
void display(int s[N][N])
{
	int i, j;
	for(i = 0; i < N; i++)
	{
		for(j = 0; j < N; j++)
		{
			// 把0当做空格输出
			if(s[i][j] > 0)
			{
				printf("%d ", s[i][j]);
			}
			else if(s[i][j] == 0)
			{
				printf("  ");
			}
		}

		printf("\n");
	}
}

// 寻找出棋盘中的空格键
void findSpace(int s[N][N], int *x, int *y)
{
	int i, j;
	for(i = 0; i < N; i++)
	{
		for(j = 0; j < N; j++)
		{
			if(s[i][j] == 0)	// 找到空格
			{
				*x = i;
				*y = j;
			}
		}
	}
}

// 空格上移
void up(int s[N][N], int x, int y)
{
	// 空格必须是处于第2行或者第3行，才能上移
	if(x >= 1)
	{
		s[x][y] = s[x-1][y];
		s[x-1][y] = 0;
	}
}

// 空格下移
void down(int s[N][N], int x, int y)
{
	// 空格必须是处于第1行或者第2行，才能下移
	if(x <= 1)
	{
		s[x][y] = s[x+1][y];
		s[x+1][y] = 0;
	}
}

// 空格左移
void left(int s[N][N], int x, int y)
{
	// 空格必须是处于第2列或者第3列，才能左移
	if(y >= 1)
	{
		s[x][y] = s[x][y-1];
		s[x][y-1] = 0;
	}
}

// 空格右移
void right(int s[N][N], int x, int y)
{
	// 空格必须是处于第1列或者第2列，才能右移
	if(y <= 1)
	{
		s[x][y] = s[x][y+1];
		s[x][y+1] = 0;
	}
}

// 采用曼哈顿距离，计算从初始状态到本状态的代价
// 曼哈顿距离指，与目标位置的水平距离和垂直距离之和
// 书上给出的代价是从起始节点S到任一节点i的路径代价g(i)
// 修改代价时，采用g(j) = g(i) + cost(i, j);
// cost(i, j)指从当前i节点到它的后继节点j的代价
// 但是这里因为每次空格操作，只会改变2个位置
// 所以cost(i, j)都相同，因此可以省略，直接计算g(j) 
void compute_cost(node *p)
{
	int i, j, m, n;

	for(i = 0; i < N; i++)
	{
		for(j = 0; j < N; j++)
		{
			// 如果有对应位置不匹配的
			// 则重头搜索出与src[i][j]匹配的p->data[m][n]
			if(p->data[i][j] != src[i][j])
			{
				for(m = 0; m < N; m++)
				{
					for(n = 0; n < N; n++)
					{
						// 搜索到与src[i][j]匹配的p->data[m][n]
						// 计算曼哈顿距离后立马结束搜索
						if(p->data[m][n] == src[i][j])
						{
							// 累加每个位置的曼哈顿距离
							p->cost += abs(m-i) + abs(n-j);
							m = N;	// 修改m值，结束搜索
							break;
						}
					}
				}
			}
		}
	}
}

// 检查close表中是否有重复的状态
int checkSame(int cmp[N][N])
{
    int i, j;
    node *p;
    for(p = close->next; p != close; p = p->next)
    {
        for(i = 0; i < N; i++)
        {
            for(j = 0; j < N; j++)
            {
                if(p->data[i][j] != cmp[i][j])
                {
                    i = N + 1;
                    break;
                }
            }
        }

        if(i == N && j == N)
        {
            return 1;
        }
    }

    return 0;
}

// 检查当前棋盘状态是否为目标状态
int checkWin()
{
    int i, j;
    for(i = 0; i < N; i++)
    {
        for(j = 0; j < N; j++)
        {
			// 检测到有不同的就立马返回，节省时间
            if(cur[i][j] != dest[i][j])
            {
                return 0;
            }
        }
    }

    return 1;
}

// 打印从初始状态到目标状态的路径
void showWin()
{
	int i = 1;
    node *p, *win;

	// 创建一个win表，用来存放路径
    win = initList();	
    if(!win)
    {
        printf("win malloc fail\n");
        return;
    }

	// 由于节点中只有father(父节点)，而打印路径是从父节点开始的
	// 所以必须先从close表选择出正确的路径，因为close中可能存放不是正确路径的节点
	// 可以唯一确定的是 close->prev 一定是目的状态，由此循环往上寻找其父节点
    for(p = close->prev; p && p != close; p = p->father)
    {
        Remove(p);	// 从close表中弹出p节点
        head_insert(win, p);	// 把p节点用头插法插入到win表中
    }

	printf("the solution as follow:\n");
	// 经过头插法创建的win表，一定是按从初始状态到目标状态的排序的
    for(p = win->next; p != win; p = p->next, i++)
    {
		printf("step %d:\n", i);
        display(p->data);
        printf("\n");
    }

    clearList(win); // 清空win表
    free(win);      // 内存回收
}

// 把当前节点(tmp) 的后继节点插入到open表中
void add(node *tmp, int cmp[N][N])
{
	node *p = initList();
				
	if(!p)
	{
		printf("malloc fail\n");
		return;
	}

	copy(cmp, p->data);	// 复制棋盘状态
	p->father = tmp;	// 修改父节点指针
	compute_cost(p);	// 修改从初始状态到本状态的代价
	head_insert(open, p);	// BFS用尾插法，DFS用头插法
}

// 从表中选择一个节点，使其代价p->cost最小
// 通常是从open表中选择，如果有多个点，则随便选一个
node *min_cost(node *head)
{
	// 空表直接退出
	if(!head || head->next == head)
	{
		return NULL;
	}

	node *p, *min;
	min = head->next; 
	for(p = min->next; p != head; p = p->next)
	{
		// 遇到更小的，就更新min
		if(p->cost < min->cost)
		{
			min = p;
		}
	}

	return min;
}

// 等代价搜索法
void UCS()
{
	printf("start UCS\n");
	node *tmp;
	int x, y, k, cmp[N][N];
    
	add(NULL, src);	// 把初始状态加入到open表中
	
	while(1)
	{
		// 如果open表为空，就可以退出了
		if(open->next == open)
		{
			printf("fail\n");
			return;
		}
		
		// 从open表中选择一个节点，使其代价p->cost最小
		tmp = min_cost(open);

		// 如果tmp为空，则说明open表为空
		// 但是一般不会出现，因为前面已经对open表进行判空处理
		// 这里写的原因就是特意为了增强算法的健壮性
		if(!tmp)	
		{
			printf("fail\n");
			return;
		}

		Remove(tmp);
		tail_insert(close, tmp);
        
		printf("now go :%d\n", ++n);

		// 打印当前搜索出的棋盘状态
        copy(tmp->data, cur);
		printf("current:\n");
		display(cur);
		
		// 检测当前棋盘状态是否为目标状态
		if(checkWin())
		{
			printf("success\n\n");
			printf("solution as follow:\n");
			showWin();
			return;
		}

		k = 0;	// 记录当前节点的后继节点个数
		findSpace(cur, &x, &y);	// 寻找当前棋盘状态的空格坐标
		
		printf("try up\n");
		// 空格必须是处于第2行或者第3行，才能上移
		if(x >= 1)
		{
			copy(cur, cmp);	// 先复制当前状态cur到cmp中
			up(cmp, x, y);	// cmp尝试向上移
			
			// 判断cmp上移后close表中是否有重复状态
			// 没有重复才可以把cmp状态加入到close表中
			if(checkSame(cmp) == 0)
			{
				k++;	// 当前节点的后继节点数加一
				add(tmp, cmp); // 把后继节点加入到open表中
				printf("can up\n");
			}
		}

		printf("try down\n");
		// 空格必须是处于第1行或者第2行，才能下移
		if(x <= 1)
		{
			copy(cur, cmp);		// 先复制当前状态cur到cmp中
			down(cmp, x, y);	// cmp尝试向下移
			
			// 判断cmp下移后close表中是否有重复状态
			// 没有重复才可以把cmp状态加入到close表中
			if(checkSame(cmp) == 0)
			{
				k++;	// 当前节点的后继节点数加一
				add(tmp, cmp); // 把后继节点加入到open表中
				printf("can down\n");
			}
		}

		printf("try left\n");
		// 空格必须是处于第2列或者第3列，才能左移
		if(y >= 1)
		{
			copy(cur, cmp);		// 先复制当前状态cur到cmp中
			left(cmp, x, y);	// cmp尝试向左移
			
			// 判断cmp左移后close表中是否有重复状态
			// 没有重复才可以把cmp状态加入到close表中
			if(checkSame(cmp) == 0)
			{
				k++;	// 当前节点的后继节点数加一
				add(tmp, cmp); // 把后继节点加入到open表中
				printf("can left\n");
			}
		}

		printf("try right\n");
		// 空格必须是处于第1列或者第2列，才能右移
		if(y <= 1)
		{
			copy(cur, cmp);		// 先复制当前状态cur到cmp中
			right(cmp, x, y);	// cmp尝试向右移
		
			// 判断cmp右移后close表中是否有重复状态
			// 没有重复才可以把cmp状态加入到close表中
			if(checkSame(cmp) == 0)
			{
				k++;	// 当前节点的后继节点数加一
				add(tmp, cmp); // 把后继节点加入到open表中
				printf("can right\n");
			}
		}

		// 如果当前状态没有后继节点，应该从close表中删除该状态
		if(k == 0)
		{
            Remove(tmp);	// 弹出当前状态
            free(tmp);		// 释放当前状态
			printf("del done\n\n");
		}
	}
}

int main()
{
	open = initList();	// 初始化open表
	close = initList(); // 初始化close表

	if(!open || !close)
	{
		printf("初始化状态失败\n");
		return  -1;
	}

	// 测试阶段建议直接定义src, init()后的src很大程度上无解
	// init();	
	printf("src:\n");
	display(src);
	
	UCS();

    // 清空open表和close表并回收内存
	clearList(open);
	clearList(close);
	free(open);
	free(close);

	printf("DFS finish\n");

   return 0;
}

运行截图

 

三、简单分析

          如果认真且仔细看完代码的程序猿同学，根据注释的讲解，可以说基本上可以看懂了，下面再来讲解一下算法的流程图和关键易错点。

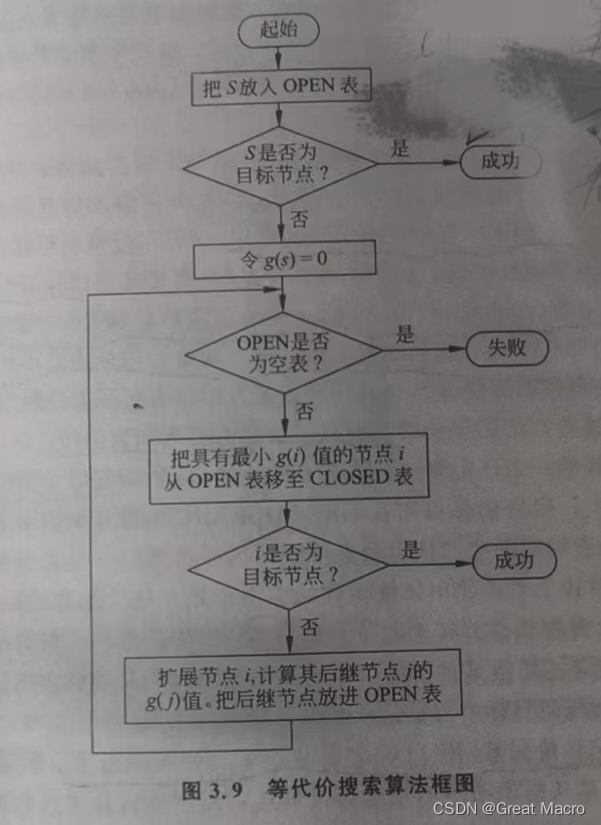
        流程图如下：

         关键易错点：

        1、open表用来存放未拓展的节点，close表用来存放已经拓展的节点，所以说，解的路径存放在close表中，但并不一定完全是close表中的节点，因为有些是其他不符合的节点。

        2、注意区分节点中的数据结构，一个版本中father指针的作用是保留父节点的指针，方便打印解的路径，而prev和next的作用是用来方便节点在链表中的操作，所以说，可以采用数组的方式来存储，此时就不需要prev和next指针了，这里不详细展开。

        3、算法结束的条件是：open表为空，即不存在任何后继节点了，此时为无解；或者当前状态就是目标状态，即找到了正确的解。

        4、空格操作的选择顺序：算法中对上移，下移，左移，右移的先后顺序要统一，不同的上下左右移动顺序会影响解的路径的长度，这点需要程序猿同学自己画图理解一下，这里比较难说明。

        5、如果存在解，则解的路径可能有多条，而使用BFS一定可以打印出一条最优解，注意用词是打印，不是搜索的过程是最优，而如果使用DFS则不一定可以打印出一条最优解，如果使用A*算法（启发式搜索）则可以保证搜索过程是最优的，自然就可以打印出一条最优解。

        6、书上给的代价计算是g(i) = g(i) + c(i, j)，从起始节点S到任一节点i的路径代价为g(i)，把从节点i到它的后继节点j的连接弧线代价为c(i，j)。但是这里有个特别的地方，就是c(i, j)都是一样的，因为从当前节点i,到后继节点j的操作是空格的上移，下移，左移，右移，这四种移动的代价都是改变两个位置，即有两个数字与上一次不同，所以所有的节点到其后继节点的代价都是一样的，因此可以不用计算c(i, j），计算c（i，j）只是为了选出最小的代价，并不是所有问题都要计算的。

所以这里直接采用计算g(i)的方法，即从初始状态到当前状态的曼哈顿距离。

        7、曼哈顿距离指，状态i与状态j之间水平距离和垂直距离之和。

四、小小总结

          本期八数码BFS求解做的有点急，但是给的代码中有一些编程小技巧，细心的可以看出来，记得收藏起来，下期出八数码A*算法求解, 下下期出八数码贪婪算法求解，敬请关注！^_^