前言
逻辑回归虽然叫回归,实际上是一个二分类模型,要知道回归模型是连续的,而分类模型是离散的,逻辑回归简单点理解就是在线性回归的基础上增加了一个 sigmoid 函数
逻辑回归 = 线性回归 + sigmoid 函数
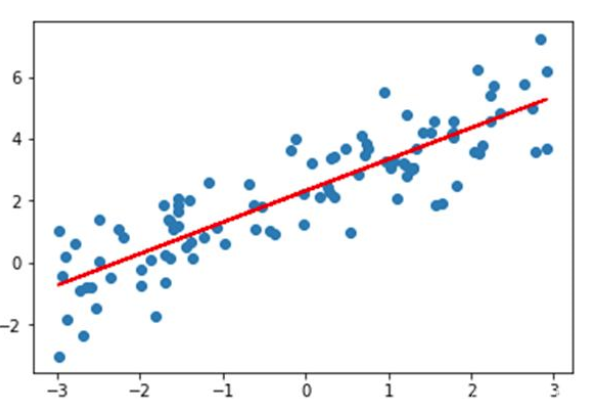
回顾线性回归
- 表达式:y=wx+by = wx + by=wx+b
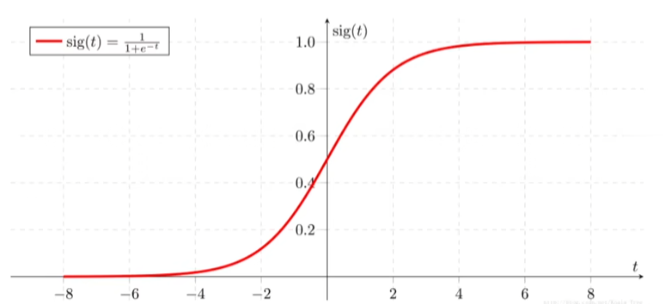
sigmoid 函数
- 什么是sigmoid 函数
-
sigmoid 是以0.5为分界线的激活函数,主要用于将结果输入sigmoid 函数中sigmoid函数会输出一个[0,1] 区间的概率值,0.5以上为一类,0.5以下为一类,这样完成二分类任务
-
公式:$sig(x) = \frac{1}{1+e^{-x}} $
逻辑回归的公式
-
z=wx+bz = wx+bz=wx+b
-
y=11+e−zy =\frac{1}{1+e^{-z}}y=1+e−z1
-
所以可以写成 y=11+e−wx+by =\frac{1}{1+e^{-wx+b}}y=1+e−wx+b1
逻辑回归的损失
- J=−[ylna+(1−y)ln(1−a)]J = -[ylna+(1-y)ln(1-a)]J=−[ylna+(1−y)ln(1−a)]
- 逻辑回归损失函数体现在“预测值” 与 “实际值” 相似程度上
- 损失值越小,模型会越好,但是过于小也要考虑过拟合的原因
梯度下降与参数更新
梯度下降:Δθj=1mXT(h−y)\Delta\theta_j=\frac{1}{m}X^T(h-y)Δθj=m1XT(h−y)
deltatheta = (1.0 / m) * X.T.dot(h - y)
更新参数:θj=θj−αΔθj\theta_j = \theta_j - \alpha\Delta\theta_jθj=θj−αΔθj
theta = theta - alpha * deltatheta
代码
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt('ex2data1.txt',delimiter=',')
x = data[:,:-1]
y = data[:,-1]
x -= np.mean(x,axis=0)
x /= np.std(x,axis=0)
X = np.c_[np.ones(len(x)),x]
def mov(theta):
z = np.dot(X,theta)
h = 1/(1+np.exp(-z))
return h
def cos(h):
j = -np.mean(y*np.log(h)+(1-y)*np.log(1-h))
return j
def tidu(sus=10000,aphe=0.1):
m,n = X.shape
theta = np.zeros(n)
j = np.zeros(sus)
for i in range(sus):
h = mov(theta)
j[i] = cos(h)
te = (1/m)*X.T.dot(h-y)
theta -= te * aphe
return h,j,theta
if __name__ == '__main__':
h,j,theta = tidu()
print(j)
plt.plot(j)
plt.show()





















 1754
1754

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








