城市交通系统智能集成方法

城市交通系统结构论证方法及智能要素的集成

摘要

城市交通系统被视为一种复杂结构，因其主要交通过程具有非-线性特征。将交通系统发展方案中不同备选方案的选择与论证方法构建为数学模型，可明确定义并论证以下内容：1）城市道路网络及公共交通线路系统的数字模型；2）区域交通经济系统的非-线性动态模型体系；3）用于预测和处理计算实验的工具。该方法可实现交通系统发展的多变量仿真。

关键词

智能交通系统，街道和道路网络，路线网络，非-线性建模，模拟

1. 引言

智能交通系统（ITS）的开发和设计旨在应对大城市道路交通、行人和乘客流量管理方面的现有挑战。

与交通管理系统相关的成本往往超过实施智能交通系统后所能获得的效益。这反映了上述流量的复杂性。潜在的风险导致了人们对传统交通管理系统的重新审视。目前，更先进的智能交通系统在俄罗斯正处于实施阶段。

在基础工程设计和试点项目期间，应研究并描述特定交通系统的复杂性，并在智能交通系统的设计阶段和实施过程中予以重视。任何交通系统均可被视为具有随机过程和确定性过程的组合，从而导致其行为复杂且难以预测，并产生相变和分岔的趋势，交通系统的非线性特性即源于此。

运输系统非-线性行为（如交通拥堵、激波、科纳理论中的相变）在科纳理论[科纳(2011)]等通常对道路交通产生负面影响。这导致了许多问题，需要立即采取应对措施。首先，这些措施并不主要涉及智能交通系统的应用，而是更为基础性的，因为许多俄罗斯城市的道路网络和交通管理存在严重缺陷。另一项工作是编制规划图的交通部分、交通发展战略、综合交通地图和交通管理计划，这些应基于对交通系统复杂运行机制的深入理解以及理论知识来解决交通系统的当前问题[加斯尼科夫 (2013)]。

需要注意的是，规划图、交通发展战略、综合交通地图、交通管理计划和智能交通系统的设计者目前缺乏可靠的方法来论证其对大城市街道和道路网络特定发展的选择，无法以最少的交通基础设施投资实现最短的延误时间和最大的通行能力。因此，自动交通管理系统和交通管理系统必须遵循最初在规划图和/或交通管理计划中确定的街道和道路网络架构。

由于主要运输过程的非线性特性，城市交通系统应被视为一种复杂结构[波普科夫（1999）]。本文旨在制定一种用于选择和论证交通系统发展方案的方法。运输系统交通系统是指城市个体与公共交通、街道和道路网络、线路图以及必要基础设施的综合系统。因此，本研究的范围是城市交通系统，研究对象是用于实施智能交通系统要素的交通系统结构验证方法。

2. 理论基础

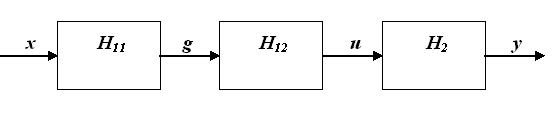
As it上文所述，交通系统既包含随机过程，也包含确定性过程。因此，该方法的第一个理论基础是宏观系统理论宏观系统 ，其中其组成部分的随机行为转化为整个系统的确定性行为[波普科夫（1999）]。下面我们考虑宏观系统的一般功能示意图（图1）。

按照宏观系统理论的惯例，图1中的х和у分别代表输入和输出，可理解为（控制）输入以及系统运行所产生的输出。内部过程g(t, z)表征系统的随机状态，而u(t, z)表示其确定性状态。其中，z为系统位置集合。表示H11描述宏观系统元素或其微观层次的随机行为，而表示H12描述随机状态g(t, z)向确定性状态u(t, z)的转换（平均操作）。状态u(t, z)与输出y(t, z)之间的关系由确定性表示H2刻画。H12与H2的组合描述系统的宏观层次。

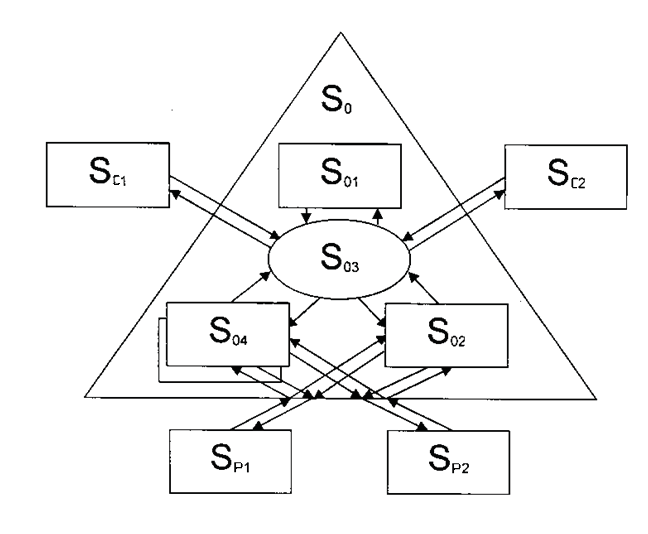
让我们以一个通用的运输系统S作为研究案例（图2）。

图2图例：S01 ——货物存储；S02 ——乘客站点；S03 ——街道和道路网络；S04 ——车库（停车位、运输企业等）；SC1 ——托运人；SC2 ——收货人；SP1 ——乘客居住地；SP2 ——乘客工作地点、服务场所等。交通系统由以下组成部分构成：网络、运输车辆等。另一个组成部分是“资源”（货物和乘客）。资源和运输车辆在交通网络中产生交通流。所有上述要素也均被表示为宏观系统。

任何运输系统都有一个经济子系统。任何经济系统中的主要过程之一是资源交换与分配过程。让我们根据论文[波普科夫（1999）]来描述运输系统S的经济子系统的运行。运输系统可以被视为一个由n个用户和m种资源组成的经济系统。在某一时刻t，分配过程导致了用户之间资源的特定分配T(t)。矩阵T的元素表示第i组用户所拥有的j型资源的数量。在任意时刻，分配过程应满足平衡比率：

$$
\sum_{i=1}^{m} T_{ij} + V_j = M_j
$$

其中 $M_j$ 为j型资源的数量，$V_j$ 为未在用户之间分配的j型资源数量。资源组与用户组之间的不同转换由相应的动机构成，这些动机具有高度非确定性。

因此，上述描述反映了任何交通系统都具有双重特征，即包含基础设施和经济子系统。

交通系统服务水平的数学建模[什韦佐夫和阿里耶夫（2003），马里沃特和穆尔（2008），阿古列耶夫等（2013）]是宏观系统理论的一个重要组成部分。交通系统服务水平的一个关键且基本的特征是，用户对交通方式和路径的选择会影响其他用户做出的类似选择。

动态混沌理论[马格尼茨基和西多罗夫(2004)]是支撑提出的方法的理论基础的第二个要素。在此理论框架下，已开发出不同运输系统的非线性动力学模型系统[阿古列耶夫（2006）、阿古列耶夫（2008）、阿古列耶夫和特罗皮娜（2011）、阿古列耶夫等。(2012)],这些模型构成了系统S的子集（见图2）。这类模型可用于实际构造算子H2 ，该算子负责宏观系统的确定性行为（见图1）。

旨在提高城市道路网络通行能力的实际措施由于预测的复杂性，往往无法产生预期结果。因此，采用了一套非线性模型来揭示实际运输系统中存在的规律性，并反映对街道和道路网络发展的投资与运输运营相对减少之间的相互关系。

3. 部分运输系统数学描述示例

我们分别作为规划图中的交通部分和交通发展战略的一部分，开发了图拉市和杜尚别市的运输系统模型[Agureev 等。（2013），Agureev 等（2016）]。这些模型利用根据交通与客流研究成果获得的数据进行了校准。解决通勤工作的交通系统服务水平问题，有助于揭示最突出的难点，并为图拉和杜尚别分别论证街道和道路网络及线路系统的发展选择（图 3）。

这些示例表明，任何关于交通系统服务负荷水平问题的解决方案都是唯一且非重复的，且依赖于特定假设，对应某种理想情况，这种情况在现实生活中以一定的概率程度发生。

服务水平负荷问题可以在网络类型学和/或交通管理计划发生变更的情况下多次解决。每次解决都将对应某个项目特定的情况。solution 关于网络类型学和/或交通管理计划的变更。这将导致交通流、道路路段平均速度、交通运行成本和延误时间的不同图表。

4. 交通系统结构的论证方法

该方法可表示为一系列问题的解决顺序，其中主要包括：1）建立城市交通系统的详细多级模型，涵盖交通与路线网络，并描述现有的交通管理要素；2）分析以往发展阶段城市交通系统的统计数据，揭示交通系统投入成本与交通流量（包括个体交通）之间的关系；3）确定未来阶段交通系统发展的目标，并制定交通系统远景发展规划，提出关于新建道路和街道布局、交通管理方法、基础设施实施、自动交通管理系统及智能交通系统要素的多种备选方案，并对每项规划措施进行成本估算；4）评估交通系统每种发展方案；5）选择并论证唯一经济可行且社会合理的方案，予以批准，作为后续决策的基础。

以图拉实施的一个方案为例[阿古列耶夫和皮什内伊（2013）]。我们进行了一系列计算实验（50个方案），通过根据规划图（图4，a）改变图拉街道和道路网络模型的结构，以揭示资本投资对街道和道路网络发展影响的规律性。在此过程中，我们选择了特定区域，制定了不同区域组合，并对建设和改造进行了成本估算。我们获得了每个方案的运输过程特征以及以下内容：

• 资本投资（百万卢布）–街道和道路网络区域的建设与重建费用；
• 运营成本（百万卢布）–所有交通用户每年在运输运营上的总成本。

每个方案在出行时间和出行速度方面的平均参数均有所不同。我们绘制了交通运行成本与资本投资之间的依赖关系图，以分析模拟方案并从中选择最合理的方案（图4，b）。图中每个点对应规划图的一种备选应用方案。如图表所示，对街道和道路网络基础设施发展的资本投资增长，导致在同一投资区间内出现大量具有不同交通过程特征的备选方案，且呈现出交通运行成本降低的趋势。

5. 结论

本文提出的方法能够在制定城市（都市区）交通系统方案时，选择最合理的替代方案之一，从而降低实施必要智能交通系统所需的成本elements。该方法的结果可应用于智能交通系统的设计。

该方法的数学基础包括以下组成部分：1）城市街道和道路网络以及公共交通线路系统的数字模型；2）作者提出的区域交通经济系统非线性动态模型体系；3）用于预测和处理计算实验的工具。该方法能够对区域运输系统的发展进行多方案模拟，包括道路网络发展的成本估算、考虑人口增长和就业变化情况下因减少街道和道路网络中的延误时间所带来的效益评估。