LeetCode - Medium - 1372

• Tree

Description

---

https://leetcode.com/problems/longest-zigzag-path-in-a-binary-tree/

You are given the root of a binary tree.

A ZigZag path for a binary tree is defined as follow:

• Choose any node in the binary tree and a direction (right or left).

• If the current direction is right, move to the right child of the current node; otherwise, move to the left child.

• Change the direction from right to left or from left to right.

• Repeat the second and third steps until you can’t move in the tree.

Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).

Return the longest ZigZag path contained in that tree.

Example 1:

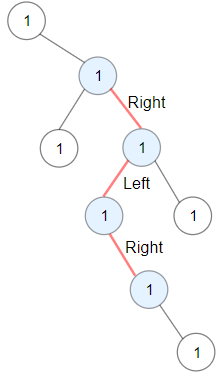
Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]

Output: 3

Explanation: Longest ZigZag path in blue nodes (right -> left -> right).

Example 2:

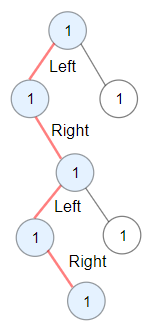
Input: root = [1,1,1,null,1,null,null,1,1,null,1]

Output: 4

Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).

Example 3:

Input: root = [1]

Output: 0

Constraints:

• The number of nodes in the tree is in the range [ 1 , 5 ∗ 1 0 4 ] [1, 5 * 10^4] [1,5∗104].

• 1 < = N o d e . v a l < = 100 1 <= Node.val <= 100 1<=Node.val<=100

Analysis

---

方法一：自己写的。

方法二：别人写的1。

方法三：别人写的2。

方法四：别人写的3。

Submission

---

import com.lun.util.BinaryTree.TreeNode;

public class LongestZigZagPathInABinaryTree {

//方法一：我自己写的

public int longestZigZag(TreeNode root) {

int[] longest = {0};

longestZigZag(root, ‘n’, 0, longest);

return longest[0];

}

//Parameter ‘relationship’ means relationship between parent and current node.

//‘n’ means no parent, specially for root node.

//‘l’ means current node is parent’s left node.

//‘r’ means current node is parent’s right node.

private void longestZigZag(TreeNode node, char relationship, int count, int[] longest) {

if(node == null) return;

//when node is a leaf.

if(node.left == null && node.right == null) {

longest[0] = Math.max(longest[0], count);

return;

}

if(node.left != null) {

int temp = count;

if(relationship == ‘l’) {

longest[0] = Math.max(longest[0], count);

temp = 0;

}

longestZigZag(node.left, ‘l’, temp + 1, longest);

}

if(node.right != null) {

int temp = count;

if(relationship == ‘r’) {

longest[0] = Math.max(longest[0], count);

temp = 0;

}

longestZigZag(node.right, ‘r’, temp + 1, longest);

}

}

//方法二：别人写的1

public int longestZigZag2(TreeNode root) {

return dfs(root)[2];

}

/**

• Recursive return [left, right, result], where:

• left is the maximum length in direction of root.left

• right is the maximum length in direction of root.right

• result is the maximum length in the whole sub tree.

• @param root

• @return

*/

private int[] dfs(TreeNode root) {

if (root == null) return new int[]{-1, -1, -1};

int[] left = dfs(root.left), right = dfs(root.right);

int res = Math.max(Math.max(left[1], right[0]) + 1, Math.max(left[2], right[2]));

return new int[]{left[1] + 1, right[0] + 1, res};

}

//方法三：别人写的2

public int longestZigZag3(TreeNode root) {

int[] maxStep = {0};

dfs(root, true, 0, maxStep);

dfs(root, false, 0, maxStep);

return maxStep[0];

}

private void dfs(TreeNode root, boolean isLeft, int step, int[] maxStep) {

if (root == null) return;

maxStep[0] = Math.max(maxStep[0], step); // update max step sofar

if (isLeft) {

dfs(root.left, false, step + 1, maxStep); // keep going from root to left

dfs(root.right, true, 1, maxStep); // restart going from root to right

} else {

dfs(root.right, true, step + 1, maxStep); // keep going from root to right

dfs(root.left, false, 1, maxStep); // restart going from root to left

}

}

//方法四：别人写的3

public int longestZigZag4(TreeNode root) {

int[] result = {0};

dfs(root, true, result);

return result[0];

}

public int dfs(TreeNode node, boolean isLeft, int[] result){

if(node == null){

return 0;

}

//try start here

int l = dfs(node.left, false, result);

int r = dfs(node.right, true, result);

result[0] = Math.max(result[0], l);

result[0] = Math.max(result[0], r);

//return sum for parent

return 1 + (isLeft ? l : r);

}