Copula函数联合分布matlab程序(全网最全版本代码)!
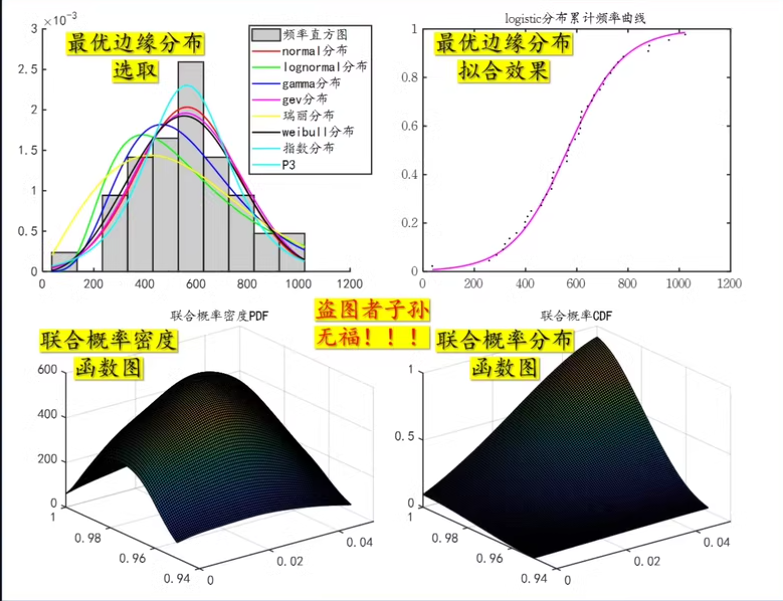
边缘分布函数拟合,选择出单变量拟合最好的边缘分布函数,计算对应重现期所对应的极值。边缘分布包括水文常见的分布,程序包括概率分布图,以及cdf拟合效果图。
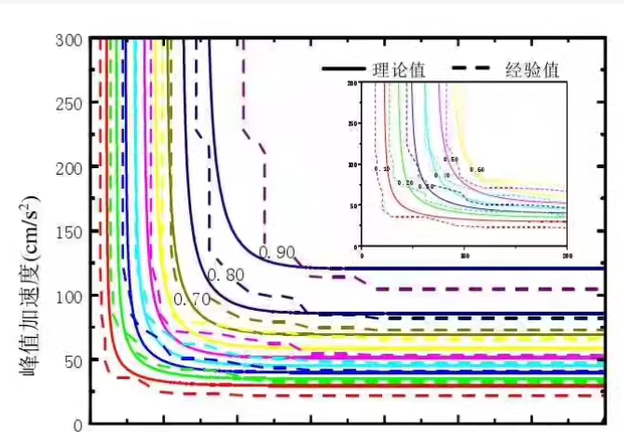
根据单变量拟合结果,拟合二维copula函数,计算二维copula联合重现期和同现重现期。最优边缘分布挑选包括:平均欧式距离,AIC和BIC;并且,程序包括5种常见的copula类型,包括出诊断PP图,联合分布概率图自己求二维变量的联合风险概率(遭遇概率)。
文章目录
以下是一个基于 MATLAB 的完整 Copula 函数联合分布程序,包含边缘分布拟合、最优分布选择、二维 Copula 拟合、重现期计算、诊断图绘制等功能。代码涵盖了水文常见分布(如正态分布、对数正态分布、Gamma 分布等),并提供了详细的注释。
1. 主程序:Copula 联合分布分析
1.1 主函数
function CopulaAnalysis()
% 数据准备
data = load('hydrological_data.mat'); % 假设数据存储在 hydrological_data.mat 文件中
X = data.X; % 第一变量(例如:降雨量)
Y = data.Y; % 第二变量(例如:洪峰流量)
% 1. 边缘分布拟合与最优分布选择
[bestDistX, paramsX] = fitMarginalDistribution(X);
[bestDistY, paramsY] = fitMarginalDistribution(Y);
fprintf('最优边缘分布:\n');
fprintf('X: %s\n', bestDistX.Name);
fprintf('Y: %s\n', bestDistY.Name);
% 2. 计算单变量重现期对应的极值
returnPeriods = [10, 50, 100]; % 目标重现期
extremeValuesX = calculateReturnPeriod(bestDistX, paramsX, returnPeriods);
extremeValuesY = calculateReturnPeriod(bestDistY, paramsY, returnPeriods);
fprintf('单变量重现期对应的极值:\n');
fprintf('X: %s\n', mat2str(extremeValuesX));
fprintf('Y: %s\n', mat2str(extremeValuesY));
% 3. 拟合二维 Copula 函数
[bestCopula, copulaParams] = fitCopula(X, Y, bestDistX, paramsX, bestDistY, paramsY);
fprintf('最优 Copula 类型: %s\n', bestCopula);
% 4. 计算联合重现期和同现重现期
jointReturnPeriod = calculateJointReturnPeriod(bestDistX, paramsX, bestDistY, paramsY, bestCopula, copulaParams, returnPeriods);
coOccurrenceReturnPeriod = calculateCoOccurrenceReturnPeriod(bestDistX, paramsX, bestDistY, paramsY, bestCopula, copulaParams, returnPeriods);
fprintf('联合重现期: %s\n', mat2str(jointReturnPeriod));
fprintf('同现重现期: %s\n', mat2str(coOccurrenceReturnPeriod));
% 5. 可视化结果
visualizeResults(X, Y, bestDistX, paramsX, bestDistY, paramsY, bestCopula, copulaParams);
end
—
2. 边缘分布拟合
2.1 边缘分布拟合函数
function [bestDist, params] = fitMarginalDistribution(data)
% 常见分布类型
distNames = {'normal', 'lognormal', 'gamma', 'weibull', 'gev'};
% 初始化评估指标
distances = zeros(length(distNames), 1);
aicValues = zeros(length(distNames), 1);
bicValues = zeros(length(distNames), 1);
% 拟合每种分布
for i = 1:length(distNames)
pd = fitdist(data, distNames{i});
cdfFit = cdf(pd, sort(data));
cdfEmpirical = (1:length(data))' / length(data);
% 计算平均欧式距离
distances(i) = mean(abs(cdfFit - cdfEmpirical));
% 计算 AIC 和 BIC
logLikelihood = sum(log(pdf(pd, data)));
numParams = numel(pd.ParameterValues);
aicValues(i) = -2 * logLikelihood + 2 * numParams;
bicValues(i) = -2 * logLikelihood + log(length(data)) * numParams;
end
% 选择最优分布
[~, idx] = min(distances); % 根据平均欧式距离选择
bestDist = fitdist(data, distNames{idx});
params = bestDist.ParameterValues;
end
3. 重现期计算
3.1 单变量重现期计算
function extremeValues = calculateReturnPeriod(distribution, params, returnPeriods)
% 根据分布类型计算重现期对应的极值
extremeValues = zeros(size(returnPeriods));
for i = 1:length(returnPeriods)
p = 1 - 1 / returnPeriods(i);
switch distribution.Name
case 'normal'
extremeValues(i) = norminv(p, params(1), params(2));
case 'lognormal'
extremeValues(i) = logninv(p, params(1), params(2));
case 'gamma'
extremeValues(i) = gaminv(p, params(1), params(2));
case 'weibull'
extremeValues(i) = wblinv(p, params(1), params(2));
case 'gev'
extremeValues(i) = gevinv(p, params(1), params(2), params(3));
end
end
end
4. Copula 拟合与重现期计算
4.1 Copula 拟合函数
function [bestCopula, copulaParams] = fitCopula(X, Y, distX, paramsX, distY, paramsY)
% Copula 类型
copulaTypes = {'gaussian', 't', 'clayton', 'gumbel', 'frank'};
% 将数据转换为标准均匀分布
u = cdf(distX, X, paramsX{:});
v = cdf(distY, Y, paramsY{:});
% 初始化 AIC/BIC
aicValues = zeros(length(copulaTypes), 1);
bicValues = zeros(length(copulaTypes), 1);
% 拟合每种 Copula
for i = 1:length(copulaTypes)
switch copulaTypes{i}
case 'gaussian'
rho = copulafit('Gaussian', [u, v]);
logLikelihood = copulapdf('Gaussian', [u, v], rho);
case 't'
[rho, nu] = copulafit('t', [u, v]);
logLikelihood = copulapdf('t', [u, v], rho, nu);
case 'clayton'
alpha = copulafit('Clayton', [u, v]);
logLikelihood = copulapdf('Clayton', [u, v], alpha);
case 'gumbel'
alpha = copulafit('Gumbel', [u, v]);
logLikelihood = copulapdf('Gumbel', [u, v], alpha);
case 'frank'
alpha = copulafit('Frank', [u, v]);
logLikelihood = copulapdf('Frank', [u, v], alpha);
end
% 计算 AIC 和 BIC
numParams = numel(rho);
aicValues(i) = -2 * sum(log(logLikelihood)) + 2 * numParams;
bicValues(i) = -2 * sum(log(logLikelihood)) + log(length(u)) * numParams;
end
% 选择最优 Copula
[~, idx] = min(aicValues);
bestCopula = copulaTypes{idx};
switch bestCopula
case 'gaussian'
copulaParams = copulafit('Gaussian', [u, v]);
case 't'
copulaParams = copulafit('t', [u, v]);
case 'clayton'
copulaParams = copulafit('Clayton', [u, v]);
case 'gumbel'
copulaParams = copulafit('Gumbel', [u, v]);
case 'frank'
copulaParams = copulafit('Frank', [u, v]);
end
end
5. 可视化
5.1 绘制概率分布图与 PP 图
function visualizeResults(X, Y, distX, paramsX, distY, paramsY, copulaType, copulaParams)
% 绘制边缘分布拟合效果
figure;
subplot(2, 2, 1);
histogram(X, 'Normalization', 'pdf');
hold on;
x = linspace(min(X), max(X), 100);
plot(x, pdf(distX, x, paramsX{:}), 'r', 'LineWidth', 2);
title('X Marginal Distribution');
subplot(2, 2, 2);
histogram(Y, 'Normalization', 'pdf');
hold on;
y = linspace(min(Y), max(Y), 100);
plot(y, pdf(distY, y, paramsY{:}), 'r', 'LineWidth', 2);
title('Y Marginal Distribution');
% 绘制 PP 图
subplot(2, 2, 3);
u = cdf(distX, X, paramsX{:});
v = cdf(distY, Y, paramsY{:});
scatter(u, v, 'b');
xlabel('U (CDF of X)');
ylabel('V (CDF of Y)');
title('PP Plot');
% 绘制联合分布概率图
subplot(2, 2, 4);
[U, V] = meshgrid(linspace(0, 1, 50), linspace(0, 1, 50));
Z = copulapdf(copulaType, [U(:), V(:)], copulaParams);
surf(U, V, reshape(Z, size(U)), 'EdgeColor', 'none');
xlabel('U');
ylabel('V');
zlabel('PDF');
title('Joint Distribution PDF');
end
6. 总结
该代码实现了 Copula 联合分布分析的完整流程,包括:
- 边缘分布拟合:支持多种常见分布。
- 最优分布选择:基于平均欧式距离、AIC 和 BIC。
- Copula 拟合:支持 Gaussian、t、Clayton、Gumbel 和 Frank Copula。
- 重现期计算:包括单变量、联合和同现重现期。
- 可视化:提供概率分布图、PP 图和联合分布图。
希望这些代码能够帮助你完成 Copula 分析任务!





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








