LeetCode通关：连刷十四题，回溯算法完全攻略_请使用回溯算法,描述求解该谜题的下列版本的主要思路并给出算法的伪代码 a 已知

本文链接：https://blog.youkuaiyun.com/2501_90253000/article/details/145217604


💡 思路：


这道题是回溯算法的经典题目。


我们来看一下这道题的抽象树形结构：


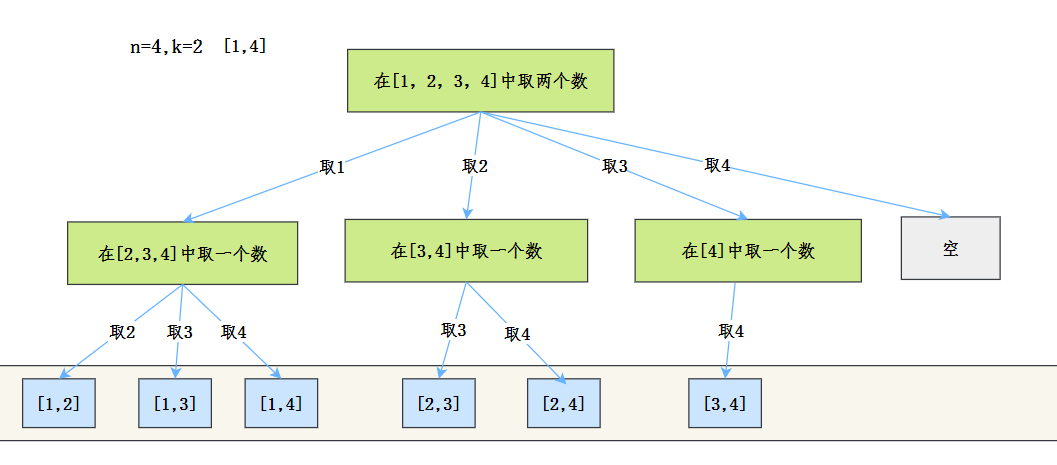
![组合抽象树结构](https://img-blog.csdnimg.cn/img_convert/afe6cac95335779a7572818505ea9819.png)


按照我们的回溯模板，看看这道题应该怎么写：


* 返回值、参数


首先方法里是一定要区间的数据，[start，n]。


计数的k也不可缺少。


最后的结果集合result，还有每条路径的结果path，可以定义全局变量，来提升可读性。


* 终止条件


什么时候终止，就是什么时候到叶子节点了呢？结果parh的大小等于k，说明到了叶子节点，一次递归结束。


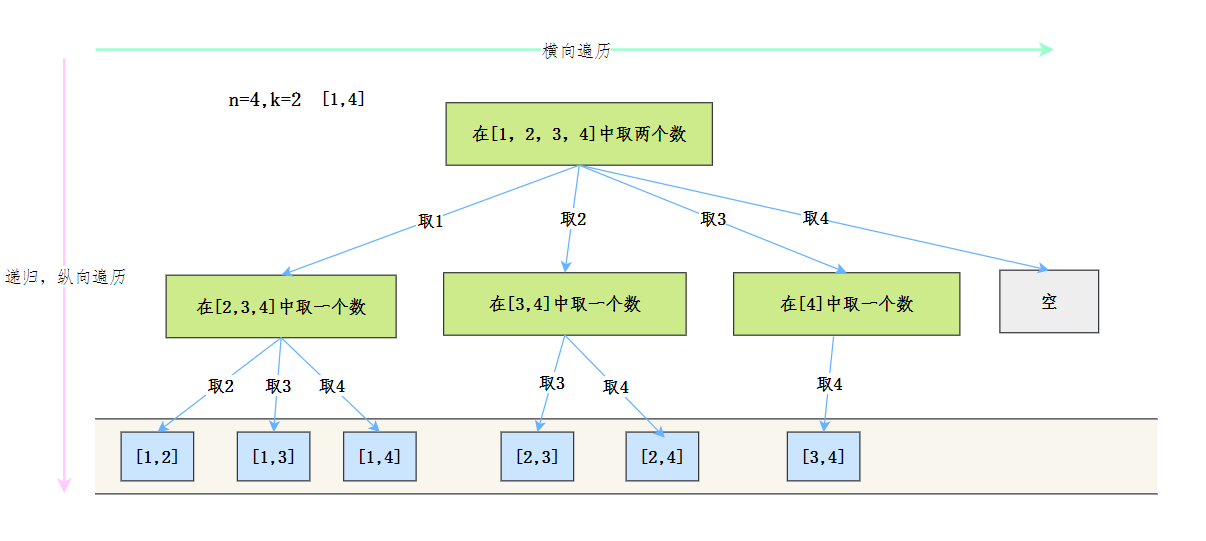
* 单层逻辑


在单层逻辑里面，我们要做两件事：


1. 遍历序列
2. 递归，遍历节点


![组合单层逻辑](https://img-blog.csdnimg.cn/img_convert/4de564c5982220be1c964c1390473999.png)


🖊 代码：

class Solution {
//结果集合
List<List> result;
//符合条件的结果
LinkedList path;

public List<List<Integer>> combine(int n, int k) {
    result = new ArrayList<>();
    path = new LinkedList<>();
    backstack(n, k, 1);
    return result;
}

//回溯
public void backstack(int n, int k, int start) {
    //结束条件
    if (path.size() == k) {
        result.add(new LinkedList<>(path));
        return;
    }
    for (int i = start; i <= n; i++) {
        path.addLast(i);
        //递归
        backstack(n, k, i + 1);
        //回溯,撤销已经处理的节点
        path.removeLast();
    }
}

}


⚡ 剪枝优化


回溯中，提高性能的一大妙招就是剪枝。


剪枝见名知义，就是在把我们的树的一些树枝给它剪掉。


例如`n = 4，k = 4`，


![剪枝优化](https://img-blog.csdnimg.cn/img_convert/8ea5cceaa7e1ad2b9942e738b96a61ba.png)


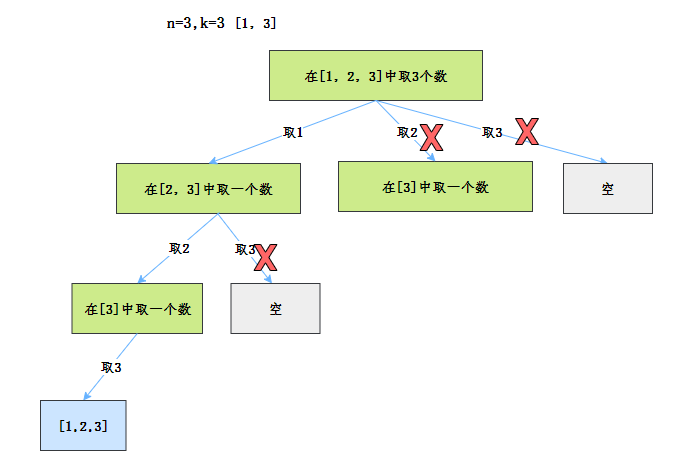
我们可以看到，有些路径，其实一定是不满足我们的要求，如果我们把这些不可能的路径`剪断`，那我们不就可以少遍历一些节点吗？


所以我们看看这道题怎么来剪这个枝：


**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索**。


1. 已经选择的元素个数：path.size();
2. 还需要的元素个数为: k - path.size();
3. 所以起始位置 : n - (k - path.size()) + 1之后的肯定不符合要求


所以优化之后的代码如下：

class Solution{
//结果集合
List<List> result;
//符合条件的结果
LinkedList path;

public List<List<Integer>> combine(int n, int k) {
    result = new ArrayList<>();
    path = new LinkedList<>();
    backstack(n, k, 1);
    return result;
}

//回溯
public void backstack(int n, int k, int start) {
    //结束条件
    if (path.size() == k) {
        result.add(new LinkedList<>(path));
        return;
    }
    for (int i = start; i <= n-(k-path.size())+1; i++) {
        path.addLast(i);
        //递归
        backstack(n, k, i + 1);
        //回溯,撤销已经处理的节点
        path.removeLast();
    }
}

}


### [LeetCode216. 组合总和 III]( )


☕ 题目：77. 组合 (https://leetcode-cn.com/problems/combinations/)


❓ 难度：中等


📕 描述：


找出所有相加之和为 ***n*** 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。


**说明：**


* 所有数字都是正整数。
* 解集不能包含重复的组合。


**示例 1:**

输入: k = 3, n = 7
输出: [[1,2,4]]


**示例 2:**

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]


💡 思路：


我们先把这道题抽象成树：


![抽象树](https://img-blog.csdnimg.cn/img_convert/70495c81213400b06abfe615502e7eb2.png)


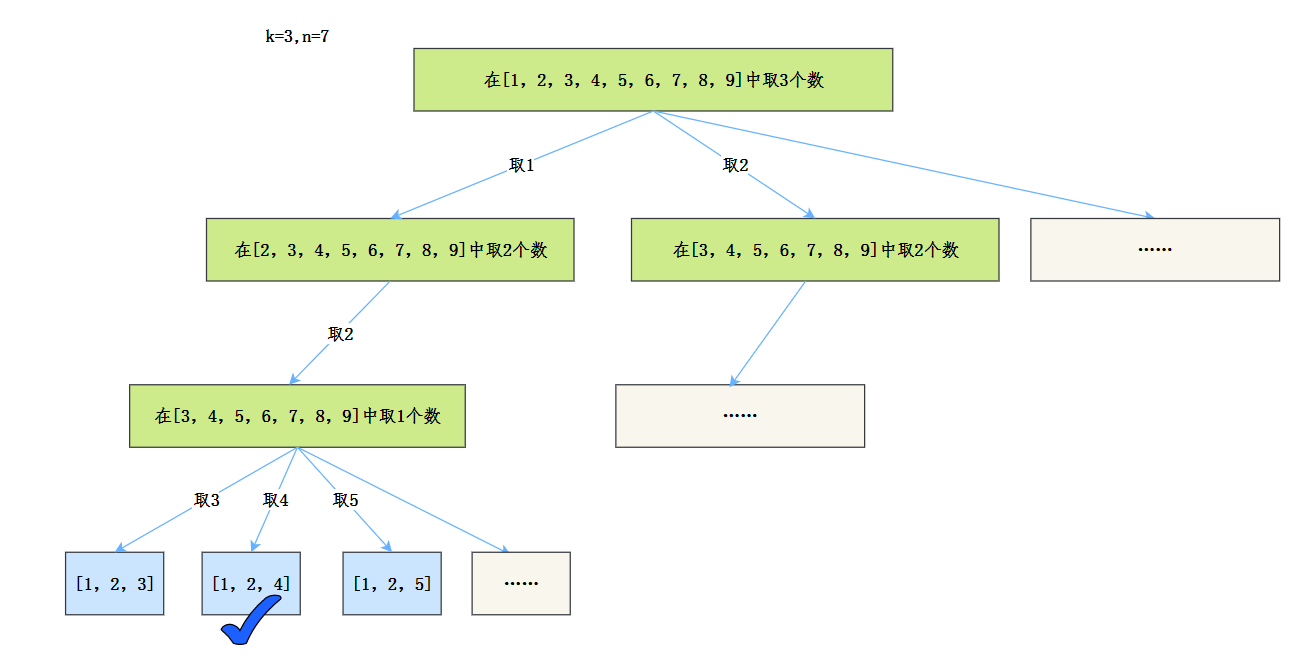
接着套模板。


* 终止条件


到叶子节点（path大小等于k）终止。


* 返回值，参数


参数稍微有变化，序列是固定的，这里的n是目标和；需要一个参数pathSum来记录路径上的数总和，我们直接全局变量。


* 单层逻辑


逻辑差别不大，回溯的时候需要把pathSum也回溯一下。


🖊 代码：

class Solution {
//结果集合
List<List> result;
//结果
LinkedList path;
//结果综合
int pathSum;

public List<List<Integer>> combinationSum3(int k, int n) {
    result = new ArrayList<>();
    path = new LinkedList<>();
    backtrack(n, k, 1);
    return result;
}

//回溯
public void backtrack(int n, int k, int start) {
    //结束
    if (path.size() == k) {
        if (pathSum == n) {
            result.add(new LinkedList<>(path));
        }
        return;
    }
    //遍历序列
    for (int i = start; i <= 9; i++) {
        path.push(i);
        pathSum += i;
        //递归
        backtrack(n, k, i + 1);
        //回溯，撤销操作
        pathSum -= path.pop();
    }
}

}


⚡ 剪枝优化


同样也可以进行剪枝优化，也很好想，如果pathNum>n ，那就没必要再遍历了。

class Solution {
//结果集合
List<List> result;
//结果
LinkedList path;
//结果综合
int pathSum;

public List<List<Integer>> combinationSum3(int k, int n) {
    result = new ArrayList<>();
    path = new LinkedList<>();
    backtrack(n, k, 1);
    return result;
}

//回溯
public void backtrack(int n, int k, int start) {
    //剪枝优化
    if (pathSum > n) {
        return;
    }
    //结束
    if (path.size() == k) {
        if (pathSum == n) {
            result.add(new LinkedList<>(path));
        }
        return;
    }
    //遍历序列
    for (int i = start; i <= 9; i++) {
        path.push(i);
        pathSum += i;
        //递归
        backtrack(n, k, i + 1);
        //回溯，撤销操作
        pathSum -= path.pop();
    }
}

}


### [LeetCode39. 组合总和]( )


☕ 题目：39. 组合总和 (https://leetcode-cn.com/problems/combination-sum/)


❓ 难度：中等


📕 描述：


给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。


candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是唯一的。


对于给定的输入，保证和为 target 的唯一组合数少于 150 个。


示例 1：

输入: candidates = [2,3,6,7], target = 7
输出: [[7],[2,2,3]]


示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]


示例 3：

输入: candidates = [2], target = 1
输出: []


示例 4：

输入: candidates = [1], target = 1
输出: [[1]]


示例 5：

输入: candidates = [1], target = 2
输出: [[1,1]]


提示：


* 1 <= candidates.length <= 30
* 1 <= candidates[i] <= 200
* candidate 中的每个元素都是独一无二的。
* 1

LeetCode通关：连刷十四题，回溯算法完全攻略_请使用回溯算法,描述求解该谜题的下列版本的主要思路并给出算法 的伪代码 a 已知

LeetCode通关：连刷十四题，回溯算法完全攻略_请使用回溯算法,描述求解该谜题的下列版本的主要思路并给出算法的伪代码 a 已知