GAT图注意力网络论文源码pytorch版超详细注释讲解！！！_pytorch gat

# build symmetric adjacency matrix 论文里A^=(D~)^0.5 A~ (D~)^0.5这个公式
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
# 对于无向图，邻接矩阵是对称的。上一步得到的adj是按有向图构建的，转换成无向图的邻接矩阵需要扩充成对称矩阵
features = normalize(features)
adj = normalize(adj + sp.eye(adj.shape[0]))   # eye创建单位矩阵，第一个参数为行数，第二个为列数
# 对应公式A~=A+IN

# 分别构建训练集、验证集、测试集，并创建特征矩阵、标签向量和邻接矩阵的tensor，用来做模型的输入
idx_train = range(140)
idx_val = range(200, 500)
idx_test = range(500, 1500)

features = torch.FloatTensor(np.array(features.todense()))  # tensor为pytorch常用的数据结构
labels = torch.LongTensor(np.where(labels)[1])
adj = sparse_mx_to_torch_sparse_tensor(adj)   # 邻接矩阵转为tensor处理

idx_train = torch.LongTensor(idx_train)
idx_val = torch.LongTensor(idx_val)
idx_test = torch.LongTensor(idx_test)

return adj, features, labels, idx_train, idx_val, idx_test

def normalize(mx):
“”“Row-normalize sparse matrix”“”
rowsum = np.array(mx.sum(1)) # 对每一行求和
r_inv = np.power(rowsum, -1).flatten() # 求倒数
r_inv[np.isinf(r_inv)] = 0. # 如果某一行全为0，则r_inv算出来会等于无穷大，将这些行的r_inv置为0
r_mat_inv = sp.diags(r_inv) # 构建对角元素为r_inv的对角矩阵
mx = r_mat_inv.dot(mx)
# 用对角矩阵与原始矩阵的点积起到标准化的作用，原始矩阵中每一行元素都会与对应的r_inv相乘，最终相当于除以了sum
return mx

def accuracy(output, labels):
preds = output.max(1)[1].type_as(labels) # 使用type_as(tesnor)将张量转换为给定类型的张量。
correct = preds.eq(labels).double() # 记录等于preds的label eq:equal
correct = correct.sum()
return correct / len(labels)

def sparse_mx_to_torch_sparse_tensor(sparse_mx): # 把一个sparse matrix转为torch稀疏张量
“”"
numpy中的ndarray转化成pytorch中的tensor : torch.from_numpy()
pytorch中的tensor转化成numpy中的ndarray : numpy()
“”"
sparse_mx = sparse_mx.tocoo().astype(np.float32)
indices = torch.from_numpy(np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
# 不懂的可以去看看COO性稀疏矩阵的结构
values = torch.from_numpy(sparse_mx.data)
shape = torch.Size(sparse_mx.shape)
return torch.sparse.FloatTensor(indices, values, shape)

## layer.py

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F

class GraphAttentionLayer(nn.Module):

def \_\_init\_\_(self, in_features, out_features, dropout, alpha, concat=True):
    super(GraphAttentionLayer, self).__init__()
    self.dropout = dropout
    self.in_features = in_features
    self.out_features = out_features
    self.alpha = alpha  #学习因子
    self.concat = concat

    self.W = nn.Parameter(torch.zeros(size=(in_features, out_features)))  #建立都是0的矩阵，大小为（输入维度，输出维度）
    nn.init.xavier_uniform_(self.W.data, gain=1.414)#xavier初始化
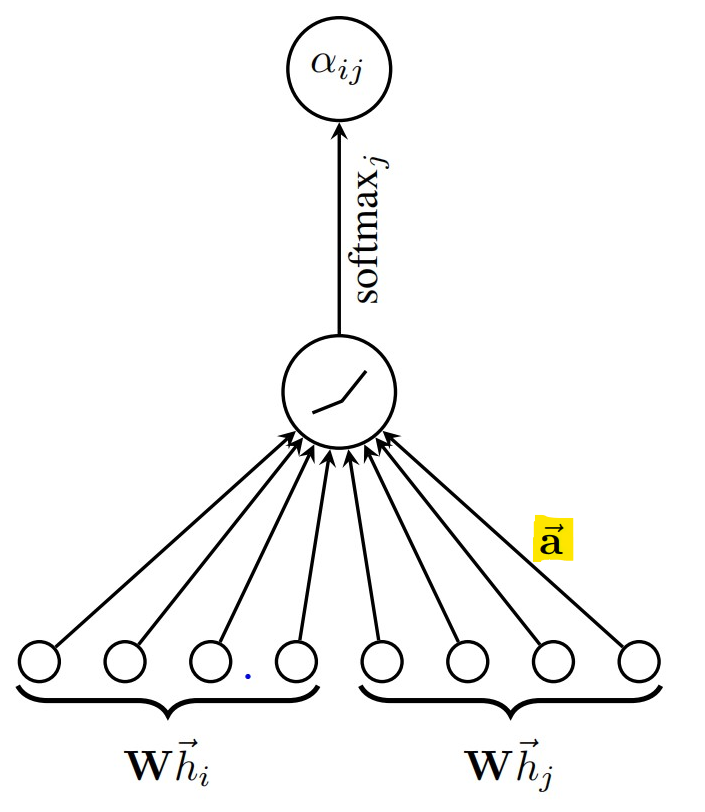
    self.a = nn.Parameter(torch.zeros(size=(2\*out_features, 1)))#见下图
    #print(self.a.shape) torch.Size([16, 1])
    
    nn.init.xavier_uniform_(self.a.data, gain=1.414)
    self.leakyrelu = nn.LeakyReLU(self.alpha)

这里的self.a,对应的是论文里的向量a，故其维度大小应该为(2\*out\_features, 1)  
 ![.](https://img-blog.csdnimg.cn/20200709204841753.png)


![在这里插入图片描述](https://img-blog.csdnimg.cn/20200709201338405.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzQ3NjUzMw=