用C语言实现杨辉三角（第一天：控制台输出）【每天进步一点点-小白学习笔记】

 给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

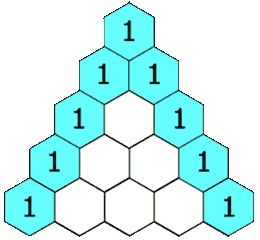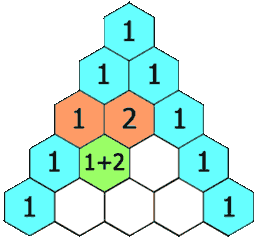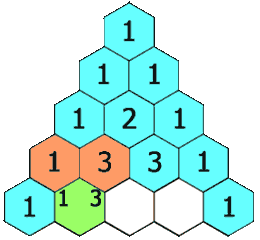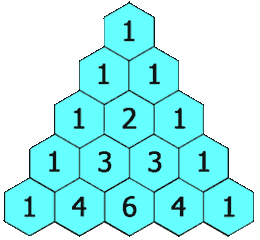
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

 1 <= numRows <= 30

第一天解题思路：

        今天是学习c语言的第一天，刚在b站看完第一节课【初识C语言】，打算用一道简单的题目作为大前期的BOSS，于是便找了这道最简单的杨辉三角。虽然作为一名刚接触编程的小白，但是杨辉三角作为最特点的数学模型之一，其简单规律还是可以大致看出来的，因此我打算根据这个规律，在第一天先简单在控制台输出杨辉三角。

        于是我开始在VS上开始尝试，首先搭建出基本框架：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>

int main(){
        // 输入行数
        int numRows;
        printf("你想输入的生成杨辉三角的最大行数为：");
        scanf("%d", &numRows);
        // 判断是否输入正确
        if (numRows < 1){
            printf("输入错误！请输入正整数！");
        }
        else{
        
        }
    }
    return 0;
}

        分析可知，杨辉三角具有以下几个规律：

        ①每行首相和末项皆为1，即a[][0]=1,a[][numRows]=1；

        ②每行第N项等于前一行的第N-1项与第N项之和，即a[M][N]=a[M-1][N-1]+a[M-1][N]；

        ③第M行的最后一项为第M项，即a[M]。

        然而这时便来了一个大难题，由于行数是输入的，而我目前所学的数组定义只能固定常量，导致我无法很好的定义这个数组进行接下来的操作，最终迫于无奈只好使用测试用例的最大值作为数组最大行列数（属于是投机取巧了，后续再完善吧）。再将规律用代码呈现如下：

#define MAX_ROWS 30  // 定义最大行数30

int arr[MAX_ROWS][MAX_ROWS];  // 建立二维数组

// 规律③：第M行的最后一项为第M项
for (int i = 0; i < numRows; i++){
    // 规律①：每行首相和末项皆为1
    arr[i][0] = 1; // 每行第一个元素
    arr[i][i] = 1; // 每行最后一个元素
    // 规律②：每行第N项等于前一行的第N-1项与第N项之和
    for (int j = 1; j < i; j++){
        arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
    }
    //循环打印
    for (int j = 0; j <= i; j++){
        printf("%d\t", arr[i][j]);
    }
    printf("\n");
}

最后将代码补全进之前写出的框架中，再套入提示与循环得出完整代码如下：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#define MAX_ROWS 30  // 定义最大行数30

int main(){
    // 1.控制台输出杨辉三角 
    while (1)  // 设置循环以当输入错误时可以重新输入
    {
     // 输入行数
     int numRows;
     printf("你想输入的生成杨辉三角的最大行数为：");
     scanf("%d", &numRows);
     // 建立二维数组
     int arr[MAX_ROWS][MAX_ROWS]; 
     // 判断是否输入正确
     if (numRows < 1){
         printf("输入错误！请输入正整数！");
         continue; // 输入错误则重新循环
     }
     else{
         // 规律③：第M行的最后一项为第M项
         for (int i = 0; i < numRows; i++){
             // 规律①：每行首相和末项皆为1
             arr[i][0] = 1; // 每行第一个元素
             arr[i][i] = 1; // 每行最后一个元素
             // 规律②：每行第N项等于前一行的第N-1项与第N项之和
             for (int j = 1; j < i; j++){
                 arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
             }
             //循环打印
             for (int j = 0; j <= i; j++){
                 printf("%d\t", arr[i][j]);
             }
             printf("\n");
             }
             break;  // 结束循环
          }
    }
    return 0;
}

运行结果如下：

就此第一天的小目标算是完成了，虽然距离题目解答完成还差了特别多，但随着后续学习，我也会不断完善，争取早日打败这第一个小BOSS进入新手期的下一阶段。