朴素贝叶斯模型

---

前言

今天我们来复习朴素贝叶斯模型，并用项目教大家快速了解朴素贝叶斯模型，我会将大家编写代码中常见的错误点在代码注释中指出，希望不会浪费大家的时间，高效学习

---

一、项目背景与数据集

• 目标：根据邮件内容判断是否为垃圾邮件（二分类问题）
• 数据集：UCI的SMS Spam Collection数据集（5574条短信，标签为ham或spam）
• 项目价值：掌握朴素贝叶斯的核心原理及其在文本分类中的应用

---

二、相关公式推导

朴素贝叶斯Naïve Bayes分类器基于贝叶斯定理Bayes' Theorem，并假设特征之间相互独立

贝叶斯定理

朴素贝叶斯假设

取对数形式

预测

拉普拉斯平滑

---

三、完整代码实现

1.加载数据集与探索

提取出数据特征，标签，以及名称等信息，并对标签分布进行可视化

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

file_path = r"D:\AIdata\spam.csv"
df = pd.read_csv(file_path, encoding='latin-1')
df = df[['v1', 'v2']]  # 只保留标签和文本列
df.columns = ['label', 'text'] # 重命名列

# 查看数据基本信息
print("数据集维度:", df.shape)
print("前5条数据:\n", df.head())
print("\n标签分布:\n", df['label'].value_counts())

# 可视化标签分布
df['label'].value_counts().plot(kind='bar', color=['skyblue', 'orange'])
plt.title("标签分布（ham=正常邮件， spam=垃圾邮件")
plt.xlabel("类别")
plt.ylabel("数量")
plt.show()

输出效果

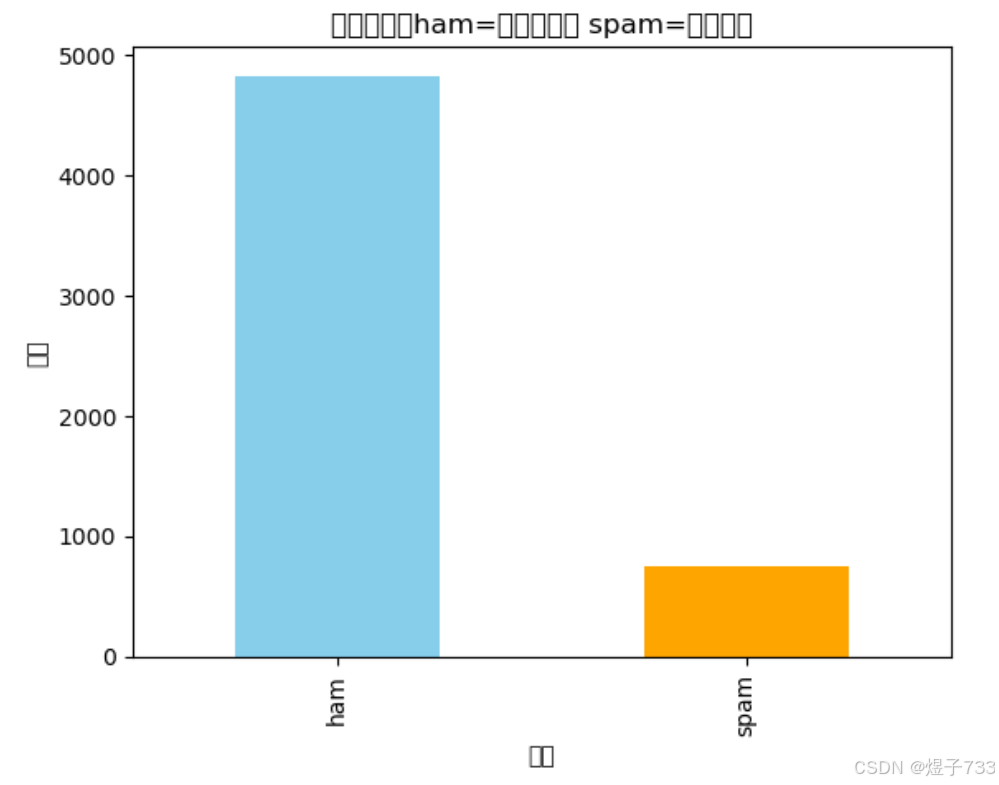
2.数据预处理

朴素贝叶斯要用到词向量数据，要先进行转换

from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer

# 将标签转为二进制
df['label'] = df['label'].map({'ham':0, 'spam':1})

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(df['text'], df['label'], test_size=0.2, random_state=42)

# 文本向量化（将文本转换为词频矩阵）
vectorizer = CountVectorizer()
X_train_vec = vectorizer.fit_transform(X_train)  # 训练集向量化
X_test_vec = vectorizer.transform(X_test)  # 测试集向量化

print("\n训练集维度:", X_train_vec.shape)
print("测试集维度:", X_test_vec.shape)

print("NaN in y_train:", np.isnan(y_train).sum()) # 查看数据中的nan值
print("NaN in X_train_vec:", np.isnan(X_train_vec.toarray()).sum())

输出效果

3.手动实现朴素贝叶斯

先计算先验概率和条件概率再计算后验概率进行预测

class NaiveBayesManual:
    def __init__(self):
        self.class_probs = {} # 类别先验概率P(y)
        self.word_probs = {} # 条件概率P(x∣y)（每个词在类别中的概率）
        
    def fit(self, X, y):
        """训练模型：计算类别先验概率和条件概率"""
        n_samples, n_features = X.shape
        self.classes = np.unique(y) # 去重后的 y
        
        # 计算类别先验概率
        for cls in self.classes:
            self.class_probs[cls] = (np.sum(y == cls) + 1) / (n_samples + len(self.classes))
            
        # 计算条件概率（拉普拉斯平滑）
        self.word_probs = {cls: np.ones(n_features) for cls in self.classes} # 用全1向量初始化，确保每个类别都有概率
        
        for cls in self.classes:
            X_cls = X[y == cls]  # 提取X中属于cls类别的样本
            if X_cls.shape[0] == 0:  # 确保X_cls不是空的
                print(f"Warning: No samples found for class {cls}")
                continue
            total_words = X_cls.sum(axis=0) + 1 # 拉普拉斯平滑
            self.word_probs[cls] = (total_words + 1) / (np.sum(total_words) + n_features)  # + n_features 保证平滑不会导致概率过大
            
    def predict(self, X):
        """预测测试集"""
        y_pred = []
        """遍历X中每个样本x，计算其属于每个类别的后验概率（即P(y∣x)）"""
        for x in X:
            posteriors = {}
            for cls in self.classes:
                if cls not in self.word_probs or np.isnan(self.class_probs[cls]):
                    continue  # 避免 NaN
                word_prob = np.where(self.word_probs[cls] > 0, self.word_probs[cls], 1e-9)  # 避免 log(0)
                # 计算后验概率（对数形式避免下溢）
                posterior = np.log(self.class_probs[cls]) + np.sum(np.log(self.word_probs[cls]) * x)
                posteriors[cls] = posterior
            # 选择后概率最大的类别
            if posteriors:
                y_pred.append(max(posteriors, key=posteriors.get))
            else:
                y_pred.append(self.classes[0])  # 备用默认类别
        return np.array(y_pred)
    
# 训练手动实现的模型
manual_nb = NaiveBayesManual()
manual_nb.fit(X_train_vec.toarray(), y_train)

# 预测测试集
y_pred_manual = manual_nb.predict(X_test_vec.toarray())

4.sklearn实现

调用模型并查看模型参数

from sklearn.naive_bayes import MultinomialNB
sklearn_nb = MultinomialNB()
sklearn_nb.fit(X_train_vec, y_train)

# 预测数据集
y_pred_sklearn = sklearn_nb.predict(X_test_vec)

# 查看模型参数（类别先验概率和条件概率）
print("\n类别先验概率:", sklearn_nb.class_log_prior_)
print("条件概率（部分）:\n", sklearn_nb.feature_log_prob_[:, :5])

输出效果

---

四、模型评估与对比

def evaluate_model(y_true, y_pred, model_name):
    acc = accuracy_score(y_true, y_pred)
    cm = confusion_matrix(y_true, y_pred)
    report = classification_report(y_true, y_pred, target_names=['ham', 'spam'])
    
    print(f"\n[{model_name}] 准确率: {acc:.3f}")
    print(f"[{model_name}] 混淆矩阵:\n", cm)
    print(f"[{model_name}] 分类报告:\n", report)

# 对比两个模型
evaluate_model(y_test, y_pred_manual, "手动实现朴素贝叶斯")
evaluate_model(y_test, y_pred_sklearn, "Scikit-learn朴素贝叶斯")

输出效果

---

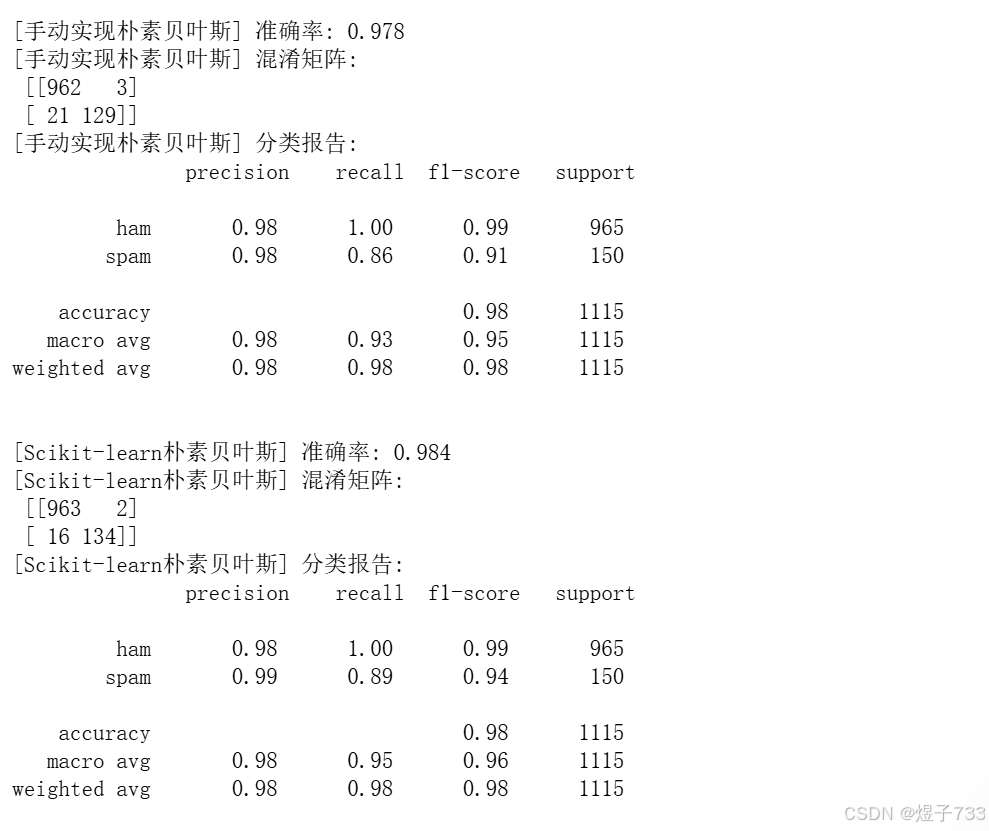
总结

以上就是今天要讲的内容，本文仅仅简单介绍了朴素贝叶斯模型的推导与实现，还有一些其他的优化朴素贝叶斯模型的方法但本文主旨是便于大家复习模型，就不再赘述

---

以上所有代码在Github仓库

结尾致敬

我是一位新手博客小白，将以复习机器学习与深度学习和强化学习模型为系列进行创作，希望能和大家一起共勉学习，如果有问题或者错误请在评论区@鼠鼠，觉得有帮助大家的可别忘了点赞加关注哦！