树与二叉树

树

树的逻辑结构

树的定义

一开始就贴个定义确实不好理解，所以先贴个图吧，通过图中的两个文本框，我们就可以知道：
1.只要构成了环形就不能称为树了
2.子树之间是不能相交的，A称为“根”
3.树的定义采用的是递归的方法，
大概知道这些就够了，我们继续。
举个例子：

我们可以把My Computer当成是根，其余的当做节点，他们之间有层序关系。

生词解释

这些都是比较重要的名词，需要全部掌握，在后面学习树和二叉树的性质时会常常出现，虽然不用我说大家也能感觉出来，由于树不同于前面的栈和队列，他们是线性的，是一对一的关系（如果有所遗忘建议回顾王卓或者懒猫老师的视频，真的是把我们当成“傻子”来教了，respect）
树却显然不是，所以这里给大家贴上一张对比图，以防混淆：

树的遍历（重要）

对于树的遍历，我们不同于前面的线性结构，这里我们分为四种：
前序（根）遍历，中序（根）遍历，后序（根）遍历，层序遍历（字面意思）
这里我习惯叫做前根遍历等等，这样就时刻提醒我遍历的顺序，同样我也建议大家这么做，确保自己能准确判断遍历输出的结果，这里只给出课后练习供大家思考：

这个答案是准确的：

树的存储结构

思考：

双亲表示法

类似用数组模拟链表的思想，正如它的名字，查找双亲的时间复杂度达到O(1)，因为除了根之外的每一个节点都存储了其双亲的信息，想要查找谁的双亲直接Pnode.parent就行了

但是如果需要查找孩子的话，需要遍历一遍树的节点，时间复杂度就是O(n)
改进方法：1.增加一个数据域firstchild记录每一个节点的第一个孩子，
但是树的双亲（区分于二叉树）可以有多个孩子，那怎样才能找到它的全部孩子呢？
2.这里再增加一个数据域表示兄弟节点，-1模拟链表为空的情况，如图：

这样我们就可以以O(1)的时间复杂度找到某个节点的所有孩子，总而的来说就是使用结构体数组来模拟链表。

孩子链表表示法

缺点十分明显，我们在定义节点的时候需要根据度最高的节点来定义孩子数据域的个数而造成空间的浪费

这里有人就要说了，这种方法还是太吃内存空间了，还有没有其他的存储方法推荐呢，有的，兄弟，有的，有人就想出最好每个节点根据度的大小来动态的调整节点大小，这种方法听起来完美，但是实际上却不如人意，首当其冲的就是我们在第一步定义结构体的时候因为节点结构不一致所以就非常困难

找孩子的好方法：

利用表头节点我们创建了一个列表，举个例子帮助大家理解一下查找过程：
比如图中A有俩孩子B和C，对应表中，A的firstchild指向的1 而1正好在表中指的是B
1的next指向2，2的指针域为空，正好对应图中B的兄弟节点是C，C右边再没有节点了，即A只有俩孩子
不难发现如果我们需要在上面找某个节点的双亲，还是需要遍历一遍数组，是比较耗时间的，类似的如果需要快速找到双亲，只需要再加一列表示每个节点的双亲即可：

主要采用了链表的静态和动态存储相结合的方式

找兄弟的好方法

依据：

二叉树

二叉树的逻辑结构

正如它的名字，二叉树就是只有两个分支的树，也就是说每个节点的度最大为2，而且还有更重要的是：它是有序地，上图中左边的两颗树中虽然都只含A.B两个元素 但是他们并不是一棵树，因此它的基本形态如下：

通过下图于上面的补充：（必须要区分树和二叉树的区别）

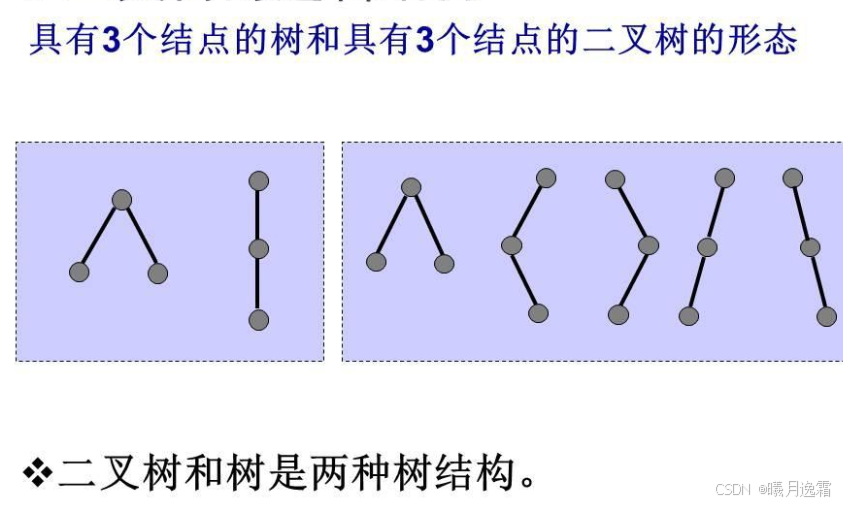
满二叉树和完全二叉树（重要）

完全二叉树的特点（重要）

二叉树性质（贼重要）

虽然图片长，但是还是希望大家耐心结合任意一个二叉树的图片进行对应，这不仅仅是性质，也是很多二叉树代码的核心，这里简单总结一下：
性质一：每一层的性质
性质二：整体层数与节点数的关系（最多2的K次幂-1，最少K）
性质三：叶子节点和度为2节点之间的关系
性质四：知道节点数怎么推出深度

证明方法大概了解就行，尤其是对于性质3,4，前面我们了解了完全二叉树是个啥东西，这里给出它的重要性质，如下：

二叉树的存储结构（重要）

顺序存储

依旧是常规操作，每学一种数据结构都需要考虑它的存储结构，一般考虑顺序和链式存储，二叉树也是如此，二叉树顺序存储的关键就在于结点的序号可以唯一的反映结点之间的逻辑关系。

对于链式存储的案例引入

对于这种斜树，如果依据前面的顺序存储，如果开辟的是静态数组空间，不仅我们在开辟空间的时候就需要事先预留好足够的空间，而且由于有很多空的结点里不能（必须要空着来反映层序关系）也没有存入数据，而造成内存极大地浪费，所以我们想到可以利用链式存储。

链式存储

• 代码：
  
• 效果图示：
  
  我们需要思考对于二叉链表中，如果一共有n个节点，那么有多少空的指针呢？
  从上往下看，一个节点包含两个指针，也就是2n个指针域，从下往上看，而对于每个（除了根之外）结点都会有一条边指向它的双亲，所以一共有n-1条边对应n-1个指针域，所以空指针域为2n-(n-1)=n+1,虽然问题简单，但是这种上下再下上的分析方法对于树这种数据结构的是非常重要的，希望大家掌握

第二个问题：二叉链表的“二叉”是什么意思呢？
这个二叉我觉得可以这么来理解：就是这个结点中指针域的个数，这个问题其实并不是只是为了问“二叉”的意思，而是对于怎样快速寻找双亲的问题产生思考，我们是不是可以类似前面的双亲孩子表示法，再加上一个parent域指向这个结点的双亲呢？因而有了三叉链表

• 静态表示方法
  
  优点：查找时间效率高，存储密度大
  缺点：不适合需要频繁插入删除的场合
  （本质上就是数组和链表基本操作在时间和空间复杂度上的区别）

二叉树存储结构及其实现代码实现

代码示例

这是我用AI优化过后的代码，主要是利用了异常捕获来优化以及对一些递归的出口做了完善，仅供参考，整体类的框架，是按照懒猫老师给的伪代码来编写的 框架用我这个就行 实测完是可以运行的，如果对C++的stl以及一些特性不太明白的朋友，可以参考最后的C语言代码手撕二叉树，希望对你有所帮助

#include <iostream>
#include <queue>
#include <stdexcept>

// 定义二叉树节点结构体
struct Binode {
    int data;
    Binode* lchild;
    Binode* rchild;
};

// 定义二叉树类
class Bitree {
public:
    // 构造函数
    Bitree();
    // 析构函数
    ~Bitree();
    // 前序遍历
    void preorder(Binode* root);
    // 中序遍历
    void inorder(Binode* root);
    // 后序遍历
    void postorder(Binode* root);
    // 层序遍历
    void levelorder(Binode* root);

    Binode* root;
private:
    // 创建二叉树的辅助函数
    Binode* create();
    // 析构函数，释放二叉树占用的内存
    void destroy(Binode* root);
};

// 构造函数，初始化二叉树
Bitree::Bitree() : root(create()) {}

Bitree::~Bitree() {
    destroy(root);
}

// 创建二叉树的辅助函数
Binode* Bitree::create() {
    int data;
    if (!(std::cin >> data)) {
        std::cerr << "Invalid input, please enter an integer." << std::endl;
        throw std::runtime_error("Invalid input");
    }
    if (data == 0)
        return nullptr;

    Binode* node = new Binode{data, nullptr, nullptr};
    try {
        node->lchild = create();
        node->rchild = create();
    } catch (...) {
        delete node; // 清理已分配的节点
        throw; // 重新抛出异常
    }
    return node;
}

// 前序遍历的辅助函数
void Bitree::preorder(Binode* root) {
    try {
        if (root == nullptr)
            return;
        std::cout << root->data << " ";
        preorder(root->lchild);
        preorder(root->rchild);
    } catch (...) {
        std::cerr << "Error occurred during preorder traversal." << std::endl;
        throw;
    }
}

// 中序遍历的辅助函数
void Bitree::inorder(Binode* root) {
    try {
        if (root == nullptr)
            return;
        inorder(root->lchild);
        std::cout << root->data << " ";
        inorder(root->rchild);
    } catch (...) {
        std::cerr << "Error occurred during inorder traversal." << std::endl;
        throw;
    }
}

// 后序遍历的辅助函数
void Bitree::postorder(Binode* root) {
    try {
        if (root == nullptr)
            return;
        postorder(root->lchild);
        postorder(root->rchild);
        std::cout << root->data << " ";
    } catch (...) {
        std::cerr << "Error occurred during postorder traversal." << std::endl;
        throw;
    }
}

// 层序遍历的辅助函数
void Bitree::levelorder(Binode* root) {
    try {
        if (root == nullptr)
            return;
        std::queue<Binode*> q;
        q.push(root);
        while (!q.empty()) {
            Binode* current = q.front();
            q.pop();
            std::cout << current->data << " ";
            if (current->lchild != nullptr)
                q.push(current->lchild);
            if (current->rchild != nullptr)
                q.push(current->rchild);
        }
    } catch (...) {
        std::cerr << "Error occurred during levelorder traversal." << std::endl;
        throw;
    }
}

// 析构函数，释放二叉树占用的内存
void Bitree::destroy(Binode* root) {
    if (root == nullptr)
        return;
    destroy(root->lchild);
    destroy(root->rchild);
    delete root;
}

int main() {
    try {
        Bitree tree;
        std::cout << "Preorder traversal: ";
        tree.preorder(tree.root);
        std::cout << "\nInorder traversal: ";
        tree.inorder(tree.root);
        std::cout << "\nPostorder traversal: ";
        tree.postorder(tree.root);
        std::cout << "\nLevelorder traversal: ";
        tree.levelorder(tree.root);
        std::cout << std::endl;  // 添加换行符
    } catch (const std::exception& e) {
        std::cerr << "Exception caught: " << e.what() << std::endl;
        return 1;
    }
    return 0;
}
************************************************************************************************分割线

```c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct TreeNode {
    char data;
    struct TreeNode* lchild;
    struct TreeNode* rchild;
} TreeNode;

void freeTree(TreeNode* root) {
    if (root == NULL) return;
    freeTree(root->lchild);
    freeTree(root->rchild);
    free(root);
}

void createTree(TreeNode** T, const char* data, int* index) {
    if (data == NULL || *index >= strlen(data)) {
        *T = NULL;
        return;
    }

    char ch = data[*index];
    (*index)++;

    if (ch == '#') {
        *T = NULL;
    } else {
        *T = (TreeNode*) malloc(sizeof(TreeNode));
        if (*T == NULL) {
            fprintf(stderr, "Memory allocation failed\n");
            exit(EXIT_FAILURE);
        }
        (*T)->data = ch;
        createTree(&((*T)->lchild), data, index);
        createTree(&((*T)->rchild), data, index);
    }
}

void preOrder(TreeNode* T) {
    if (T == NULL) {
        return;
    } else {
        printf("%c ", T->data);
        preOrder(T->lchild);
        preOrder(T->rchild);
    }
}

void inOrder(TreeNode* T) {
    if (T == NULL) {
        return;
    } else {
        inOrder(T->lchild);
        printf("%c ", T->data);
        inOrder(T->rchild);
    }
}

void postOrder(TreeNode* T) {
    if (T == NULL) {
        return;
    } else {
        postOrder(T->lchild);
        postOrder(T->rchild);
        printf("%c ", T->data);
    }
}`