【进制及其运算——汇编前的准备】

进制学习与汇编语言的关系

虽然进制学习不是汇编语言的一部分，但在学习和使用汇编语言时，理解不同数制是非常重要的，原因如下：

1. 数据表示：在汇编语言中，数据经常以二进制或十六进制的形式表示。例如，内存地址、寄存器值和指令码通常用十六进制表示。
2. 位操作：汇编语言中经常需要进行位操作，如位移、按位与、按位或等。这些操作通常基于二进制数制。
3. 指令编码：汇编语言指令的编码通常也是基于二进制或十六进制。理解这些编码有助于更好地编写和调试汇编程序。                                                                        

进制书写

N进制的定义，由N个符号组成，逢N进一。每个进制相互独立，都是完美具有优势的，生活中我们常用十进制，在程序学习中，我们不能仅仅只使用十进制，要学会书写不同的进制，掌握用法及其转换，会简单的计算，在学习中一起探索进制的奥妙，发现不局限于十进制的神奇之处。

例如三进制（0、1、2）

 三进制顾名思义逢三进一，由0、1、2组成，下面列举三进制书写的前十五个数（表1）

三进制书写

0	1	2
10	11	12
20	21	22
100	101	102
110	111	112

                                                                         表1

 

书写原理讲解：从0到2满三位进一，所以由第一行最后的2到第二行的开始变成了10，相当于0、1、2满三位要开始进一，于是找2的下一位进位发现是0，因此写入0，0写完没有了目前的数只有0，所以一位数占满开始从两位数写，接着从1开始，写为10然后后面顺位11、12；同理10、11、12满三位继续进位，先从12中的尾数2找下一位发现是0，接着从12中的1开始进位找下一位发现是2，最终按反着的顺序书写为20（进位时从后往前依次进位，也就是从右向左写），后面的书写依次类推（图1）。

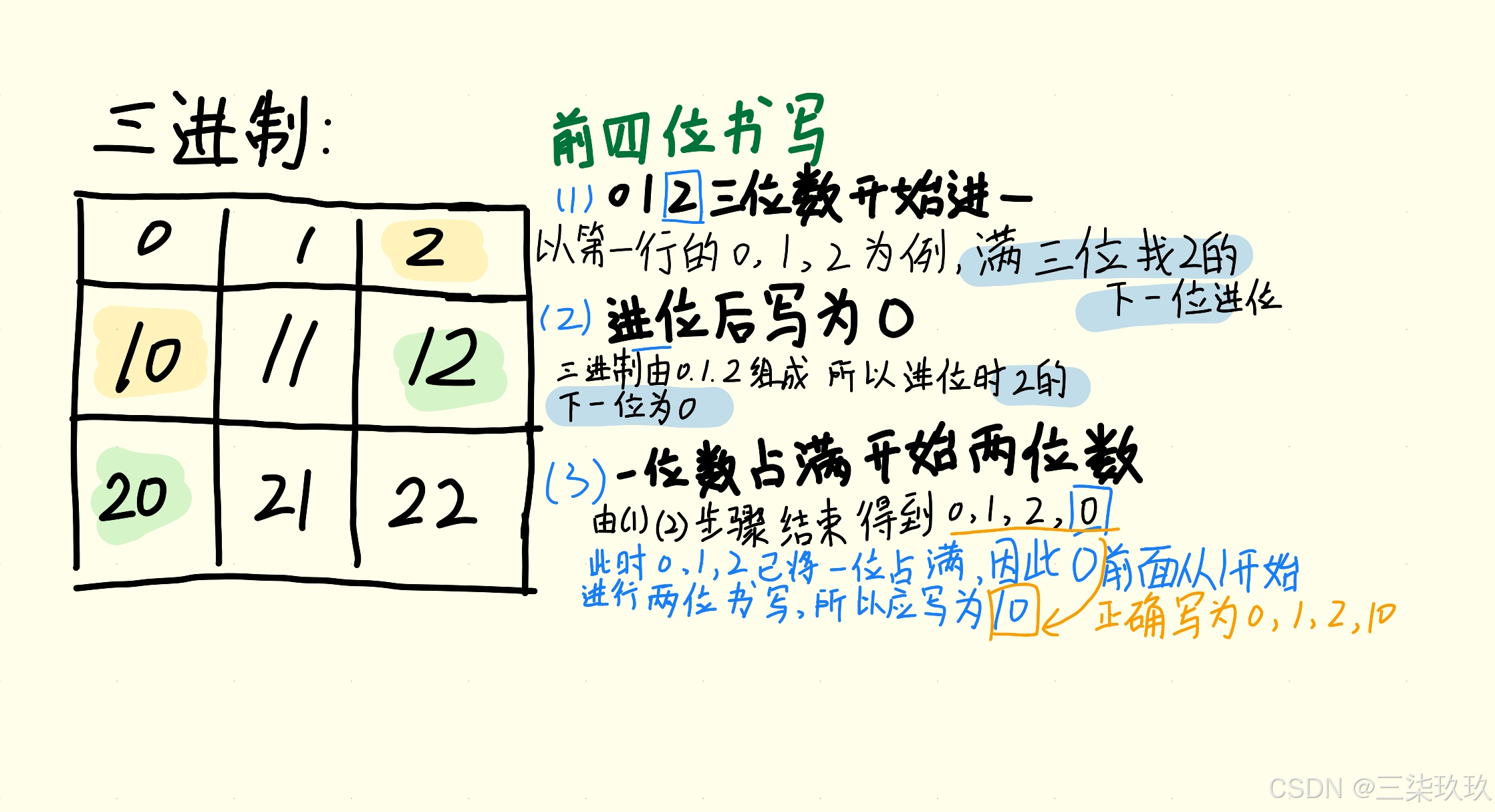图1.0

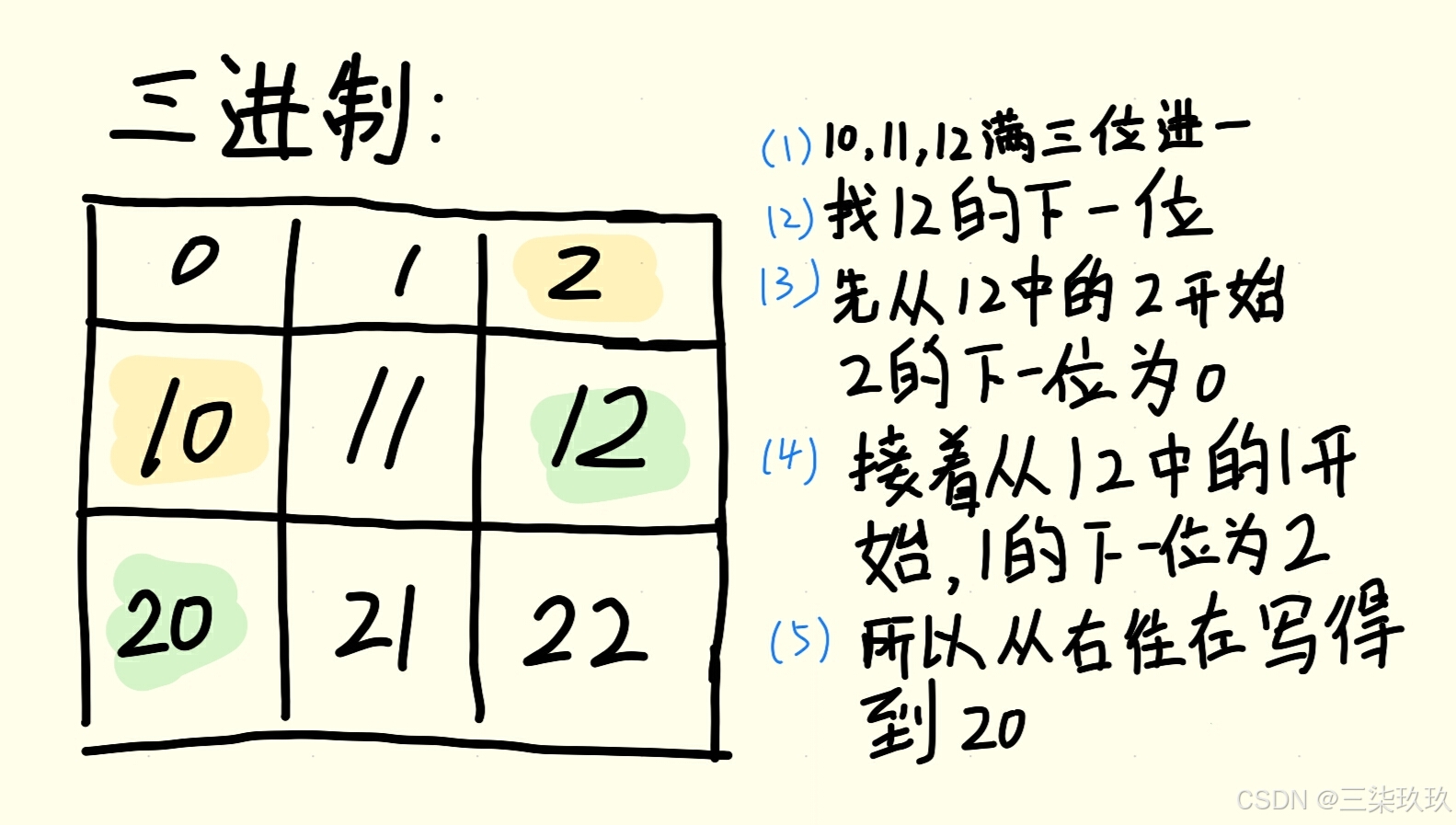
                                                                      图1.1

进制运算

例如八进制（0、1、2、3、4、5、6、7）

八进制前24个：0、1、2、3、4、5、6、7、10、11、12、13、14、15、16、17、20、21、22、23、24、25、26、27

简单计算：2+3 = 5     2*3 = 6     4+5 = 11    4*5 = 24

2+3中相当于两个三相加或三个二相加，也就是从0开始向右连续数三个数两次得到数字5，即第一次数三个数到2第二次接着从2再数三个数得到5或从3开始向右连续数两个数三次得到5，即第一次数两个到1接着从1再数两个到3，再从3再数两个到5，同理4+5也是。

2*3相当于从2开始再数两个数两次或从3开始再数三个数一次，也就是从2开始再到后面再数的两次总共三次表示3*2或者从3开始到后面再数的一次总共两次，表示2*3，分别得到的结果都是6，同理4*5也是。

多位数计算：277+333 = 632   236-54 =162   276 * 54 =20250   234 / 54 = 47

进制计算中减法等同于加法计算，刚开始接触计算，熟悉进制对应的加法进制表（如八进制加法表），可对照着进行运算并作为检查，学会了加法计算便学会了减法计算，如下面的图解，减法是借助加法，反过来思考。会书写每个进制进行简单计算，那么多位数计算便不是问题。

例如277+333 = 632

例如236-54 =162

                     八进制加法表

1+1 = 2
1+2 = 3	2+2 = 4
1+3 = 4	2+3 = 5	3+3 = 6
1+4 = 5	2+4 = 6	3+4 + 7	4+4 = 10
1+5 = 6	2+5 = 7	3+5 = 10	4+5 = 11	5+5 = 12
1+6 = 7	2+6 = 10	3+6 = 11	4+6 = 12	5+6 = 13	6+6 = 14
1+7=10	2+7 = 11	3+7 = 12	4+7 = 13	5+7 = 14	6+7 = 15	7+7 = 16

如上面的加减法一样，掌握了乘法那么除法便学会了，在乘法的基础上进行除法计算，同样也是借助乘法反过来思考除法，计算时可对照下面的八进制乘法表检查。再乘法中，将得到的各个结果相加时也是运用相应的进制加法，例如八进制中用相应的八进制加法相加而不是我们用的十进制，避免惯性计算使结果出错。

例如276*54 = 20250              

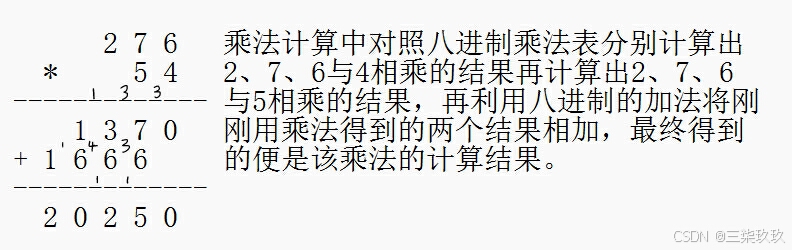
  如234/54 = 47

                     八进制乘法表 

1*1 = 1
1*2 = 2	2*2 = 4
1*3 = 3	2*3 = 6	3*3 = 11
1*4 = 4	2*4 = 10	3*4 = 14	4*4 = 20
1*5 = 5	2*5 = 12	3*5 = 17	4*5 = 24	5*5 = 31
1*6 = 6	2*6 = 14	3*6 = 22	4*6 = 30	5*6 = 36	6*6 = 44
1*7 = 7	2*7 = 16	3*7 = 25	4*7 = 34	5*7 = 43	6*7 = 52	7*7 = 61

进制简写形式

二进制中只有1和0，计算机只能理解0和1这两个二进制数字，因为计算机是一种数字电路系统，数字电路只能处理二进制数值。在数字电路中，信号只有两个状态，即开或关，对应着逻辑电平的高电平和低电平，就类似于0和1代表这两种状态。计算机通过这两个状态来表示信息和控制信号，以实现各种功能。

二进制形式

一个字节中二进制范围为0000 0000----1111 1111，相当于一次写8个数字，相比较下有些长，因此十六进制便有了这方面的好处。

十六进制形式

0、1、2、3、4、5、6、7、8、9、A、B、C，D、F

十六进制是二进制的简写形式

相当于十六进制的0--------F对应二进制的0000---------1111，一个F代表1111，将二进制的书写简洁化。

 

【以上为个人学习笔记，参考不同学习视频进行的总结】