AcWing 843.n-皇后问题

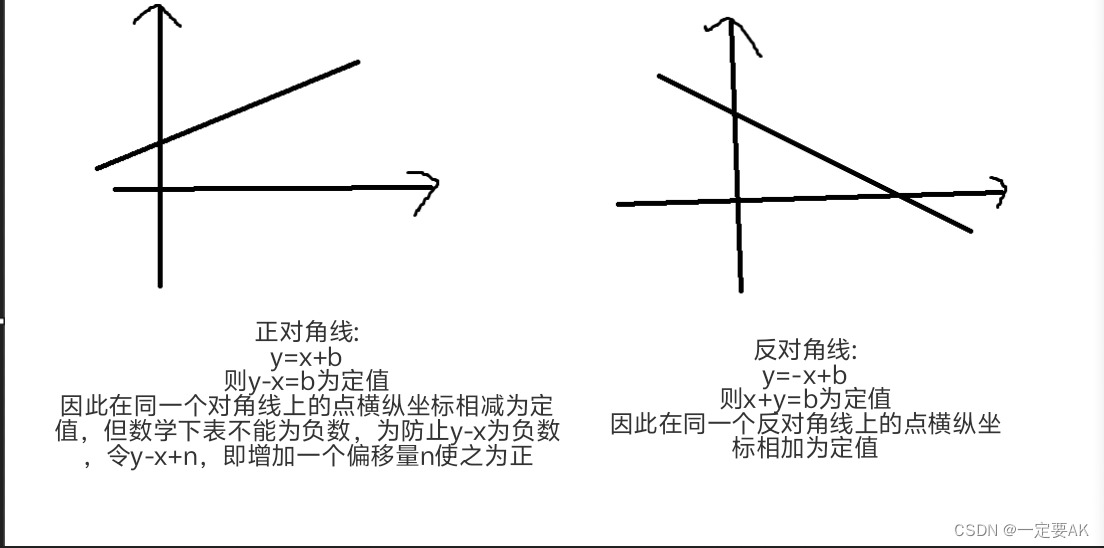
1. 对角线：每一个从左上到右下的对角线上的点横纵坐标相减相等，因为数组下标不能为负 数，所以加上个n保持正数。
2. 反对角线：每一个从左上到右下的对角线上的点横纵坐标相加相等。
3. i + r 和 n - i + r 是斜线和反斜线的斜距，左下到右上的斜线，同一条上，横纵坐标之和不变，即dg数组的同一格；左上到右下斜线同理，udg数组的同一格，从而来限制每一个皇后都不是同一条斜线。
4. puts(g[i]) :用来输出一个字符数组 g[i] ，这个数组被当作一个字符串处理。代码中的 g 是一个二维字符数组，但puts(g[i]) 被放在一个循环中，循环遍历数组 g 的每一行，puts(g[i]) 都会输出这一行的内容，并在每次输出后添加一个换行符，从而在控制台上打印出整个棋盘。
5. puts(""); :这是一个输出空行的操作。因为题中要求每个方案输出后，要输出一个空行。
6. puts 是一个标准库函数，用于输出字符串，并在输出结束后自动添加一个换行符。

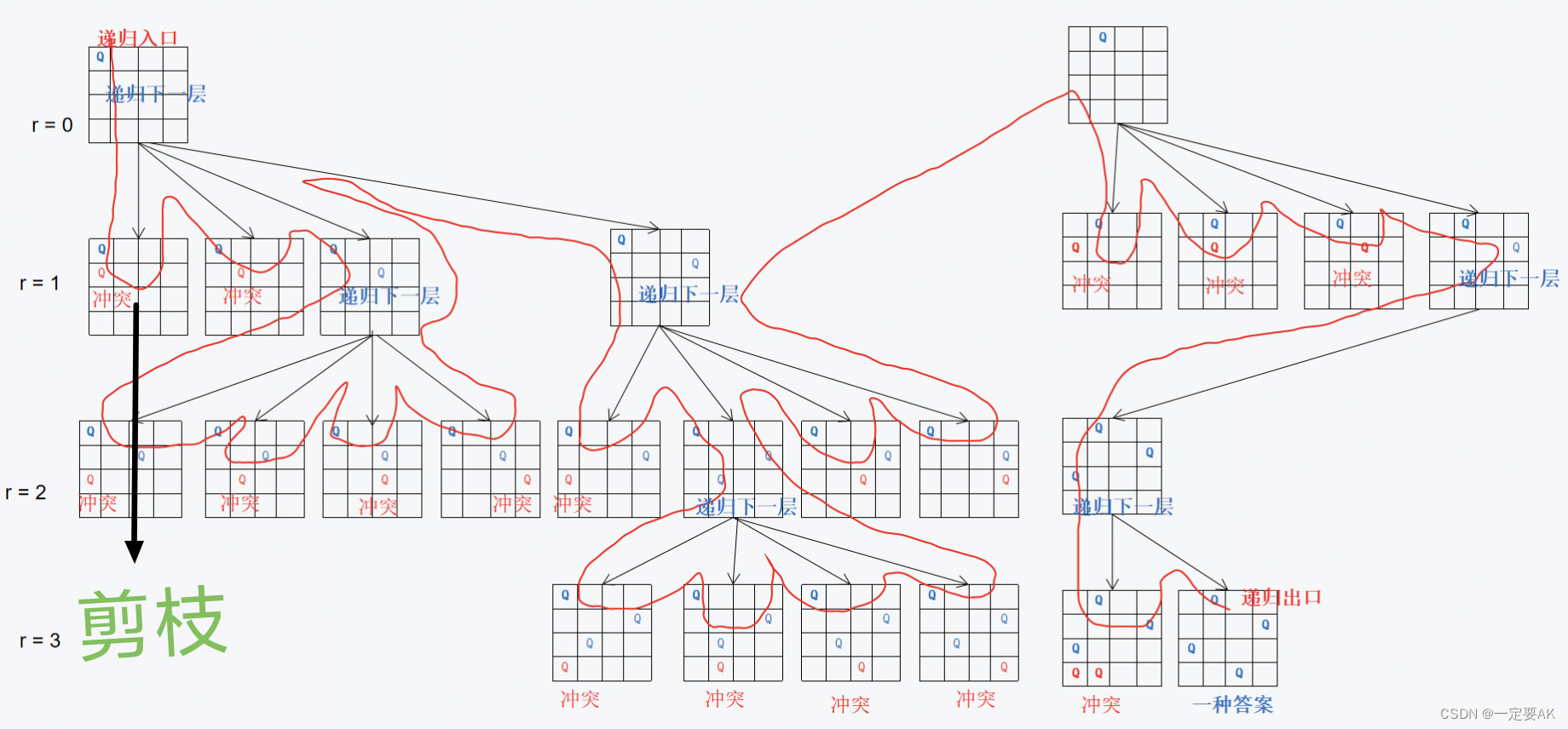
7. 剪枝:在算法中，是一种优化技术，特别是在搜索算法和优化问题中使用。目的在于减少算法需要处理的候选解的数量，通过提前排除那些不可能产生最优解或者不符合特定条件的候选解，从而减少计算资源的消耗，提高算法的效率。

剪枝类型:

1. α-β剪枝：这是在博弈树搜索中常用的一种剪枝技术，特别是在国际象棋、围棋等棋类游戏的算法中。α-β剪枝通过比较当前节点的α（对手的最佳选择）和β（自己的最佳选择）值来剪去那些不会影响最终决策的分支。

2. 分支限界法：在解决优化问题时，分支限界法通过系统地枚举所有可能的候选解空间树的分支，来寻找最优解。在搜索过程中，如果某个分支的解不可能比当前已知的更好，那么这个分支就会被剪枝。

3. 回溯法中的剪枝：回溯法是一种通过试错来寻找所有解的算法，它在搜索过程中，如果发现当前路径不可能产生有效的解，就会回溯到上一个节点，尝试其他可能的路径。在这个过程中，剪枝操作帮助算法避免无效的搜索。

#include<iostream>
using namespace std;
const int N=20;
int n;
char g[N][N];//存储棋盘
bool col[N],dg[N],udg[N];//用来标记每一列，每一条对角线，每一条反对角线上是否有皇后，1代表有，0代表无
void dfs(int u){
	if(u==n){  //由题可知，每一行都会有一个皇后，u==n代表每一行都已经放过皇后，棋盘完整
		for(int i=0;i<n;i++) puts(g[i]);//输出棋盘
		puts(" ");       //每个方案输出完成后，输出一个空行
		return;
	}
	for(int i=0;i<n;i++){   //开始判断第u行的第i列是否放皇后
		if(!col[i]&&!dg[u+i]&&!udg[n-u+i]){  
			g[u][i]='Q';        //不冲突，放皇后
			col[i]=dg[u+i]=udg[n-u+i]=1;//将该行，该点所对应的对角线和反对角线标记为1，代表有皇后了
			dfs(u+1);   //递归到下一行
			col[i]=dg[u+i]=udg[n-u+i]=0;  //回溯，清除标记
			g[u][i]='.';  //将该位置的‘Q’改为‘.’恢复现场
		}
	}
}
int main(){
cin>>n;
for(int i=0;i<n;i++){
	for(int j=0;j<n;j++){
		g[i][j]='.';  //输入棋盘的起始状态，每个方格状态均为空
	}
}
dfs(0);
return 0;	
}