AcWing 836.合并集合(并查集)

 

并查集:

可以快速的支持以下操作:

1.将两个集合合并

2.询问两个元素是否在一个集合中

思想：

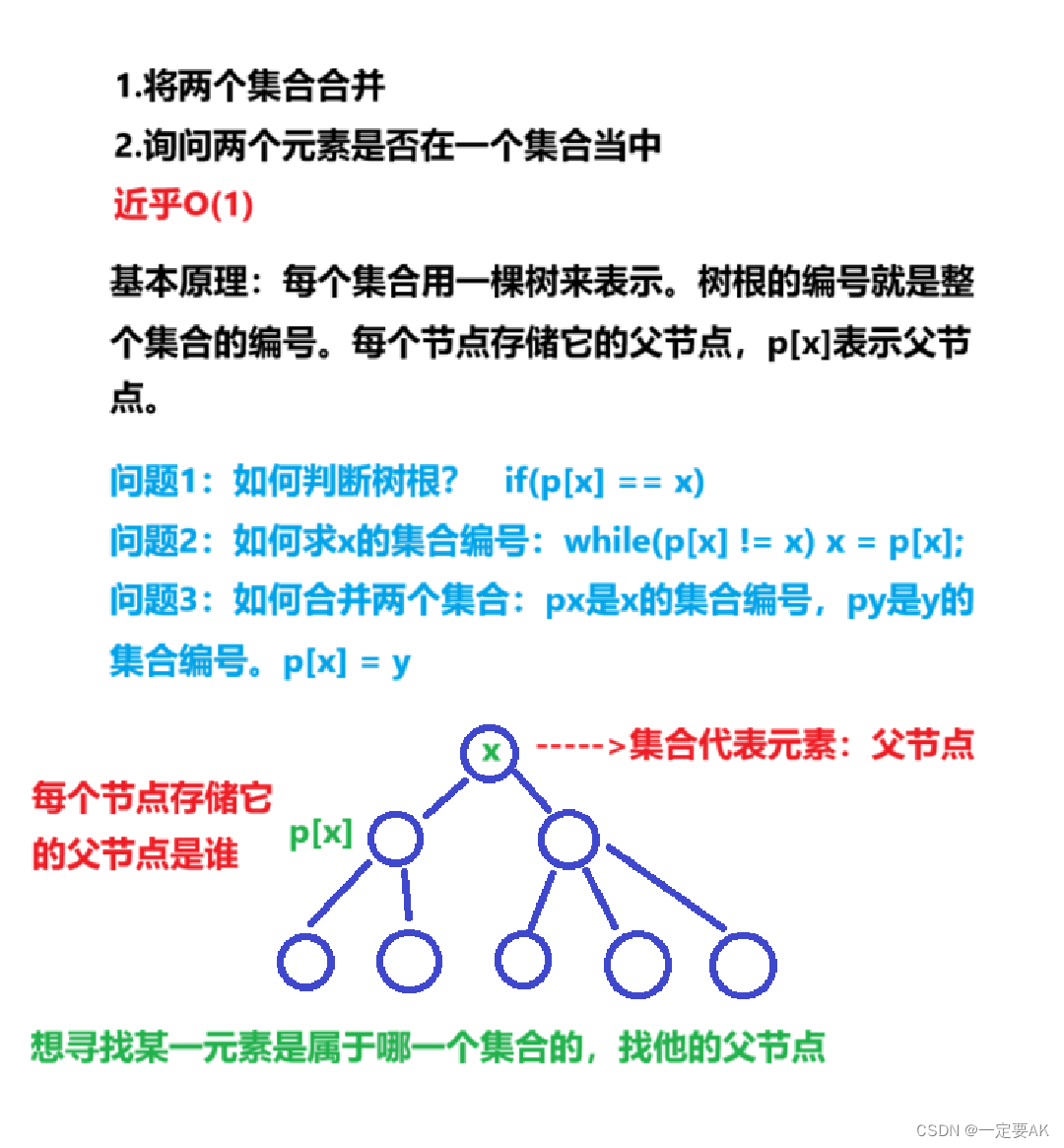
可以用树的形式来存一个集合，每个集合的编号是跟节点的编号，对于每一个点，都存一下他的父节点P;，这样要求他属于哪一个集合的时候，就可以找他的父亲，一直往上找，就找到根节点了，就知道是属于哪个集合了。

判断树根:

我们最初可以让Px =x，只有有父节点之后Px才会变，但根节点是没有父节点的，所以只要P,x== x，x就是根节点。

if (p[x] == ×) 是根节点；else 不是根节点；

求的集合编号

按照最初的思想求就行。

while (p[x] != x)x= p[x];x现在就是编号；

合并两个集合

直接让一个集合的根节点认另一个做爸爸

p[x]= y;

模板

int find(int x){ // 返回x所在集合的编号（祖宗节点）+ 路径压缩。

    if (p[x] != x) p[x] = find(x);

    return p[x];

}

 

强调:

1. op要定义成op[2]，而不是直接写op:op[2]就是读入字符串，可以规避掉意料之外的输入，如空格之类的。
2. find（x）函数找x的祖宗结点:
   重要的是p[x]的值，存的是当前所在集合的祖宗结点,当p[x]=x,表示这个数就是祖宗结点，你把两个不同集合中的两个数a，b传给分别find，返回的是两个集合的祖宗结点值。你可以想象成原来的集合里的一个数在find找它的祖宗结点，找到原来的祖宗结点，此时它的p[x]!=x,代表他不是祖宗结点，还会继续往下面找，直到找到它现在的祖宗结点为止
3. 两者合并问题:令一个p【祖宗结点】=另外一个祖宗结点的值，两个集合就合并了。

4. #include<iostream>
   using namespace std;
   const int N=100010;
   int n,m;
   int p[N];
   int find(int x){  //返回x的祖宗节点+路径压缩
   	if(p[x]!=x) p[x]=find(p[x]);//找到祖宗节点之后，直接指向祖宗节点（就是路径压缩）
   	return p[x];
   }
   int main(){
   	cin>>n>>m;
   	for(int i=1;i<=n;i++) p[i]=i;
   	while(m--){
   		char op[2];
   		int a,b;
   		cin>>op>>a>>b;
   		//集合合并
   		if(op[0]=='M') p[find(a)]=find(b);
   		//判断 a 和 b的两个数是否在同一个集合中
   		else{
   			if(find(a)==find(b)) cout<<"Yes"<<endl;
   			else cout<<"No"<<endl;
   		}
   	}
   	return 0;
   }