图像识别技术与应用课后总结（3）

感知机

美国学者FrankRosenblatt在1957年提出来的。

给予输入x，权重w和偏差b；感知机输出：

权重控制输入信号的重要程度，偏置则调整神经元被激活的难易程度。与回归（输出实数）和Softmax（输出多分类概率）不同，感知专注于二分类任务。

 w称为权重：控制输入信号的重要性的参数

b称为偏置：偏置是调整神经元被激活的容易程度参数

二分类(0或1)

Vs.回归：输出实数

Vs.Softmax：输出的概率，多个分类

感知机应用:简单逻辑电路

 

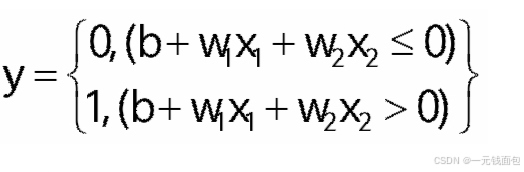
与门

与与门逻辑相反，输入全为1时输出0，其他情况输出1 。参数(-0.5, -0.5, 0.7)可实现该逻辑。

与非门

 

与与门逻辑相反，输入全为1时输出0，其他情况输出1 。参数(-0.5, -0.5, 0.7)可实现该逻辑。

或门

 

只要x_1和x_2中有一个为1，输出y就为1，仅当两者都为0时输出0 。(0.5, 0.5, -0.3)的参数设置可满足或门逻辑。

 训练过程：训练时，通过反向传播算法，计算预测结果与真实标签的误差，将误差从输出层反向传播至各层，调整神经元连接权重，降低误差，提升识别准确率。

在此基础上，多层感知机是由多个单层感知机堆叠而成，增加了隐藏层。隐藏层可学习更复杂的特征表示，解决单层感知机无法处理的非线性可分问题，如异或门问题，在图像识别、语音识别等复杂任务中有广泛应用。

异或门

 用感知机实现这个异或门的话，应该设定

什么样的权重参数呢?

假设隐藏层有两个神经元h_1、h_2，输出层一个神经元o_1。可行的权重和偏置设置如下：

隐藏层神经元h_1：连接输入的权重w_{11}=1，w_{12}=1，偏置b_1 = -1.5 。计算h_1的输出a_{h1}=w_{11}x_1 + w_{12}x_2 + b_1 ，经激活函数（单位阶跃函数，a_{h1}\leq0时输出0，a_{h1}>0时输出1 ）得到h_1的值。此神经元实现“与”逻辑。

隐藏层神经元h_2：连接输入的权重w_{21}=1，w_{22}=1，偏置b_2 = -0.5 。计算h_2的输出a_{h2}=w_{21}x_1 + w_{22}x_2 + b_2 ，经激活函数得到h_2的值。此神经元实现“或”逻辑。

输出层神经元o_1：连接隐藏层的权重w_{31}=-1，w_{32}=-1，偏置b_3 = 0.5 。计算o_1的输出a_{o1}=w_{31}h_1 + w_{32}h_2 + b_3 ，经激活函数得到最终输出y。此神经元实现“与非”逻辑。

 

验证

以x_1 = 0，x_2 = 0为例：

对于h_1，a_{h1}=1\times0 + 1\times0+(-1.5)= -1.5，h_1 = 0。

对于h_2，a_{h2}=1\times0 + 1\times0+(-0.5)= -0.5，h_2 = 0。

对于o_1，a_{o1}=(-1)\times0+(-1)\times0 + 0.5=0.5，y = 1。

其他输入组合也可依此验证，从而实现异或门功能。

感知机局限性

 

感知机的局限性：感知机的局限性就是只能表示由一条直线分割的空间。

面对这种线性不可分的情况该怎么办呢?

用非线性的曲线划分出非线性空间

——多层感知机：最简单的深度神经网络

单隐藏层

单分类

 单隐藏层突破了单层感知机的线性局限。单层感知机只能处理线性可分问题，而添加隐藏层后，模型可通过激活函数引入非线性因素，划分非线性空间，从而处理复杂的分类任务。同时，它增加了模型的复杂度和参数数量，提升了模型的表达能力。

激活函数

 

激活函数在神经网络中至关重要，它将输入信号总和转换为输出信号，决定神经元的激活方式。理想的激活函数应具备连续并可导（允许少数点不可导）的非线性特性，函数及其导函数要简单以提升计算效率，且导函数值域需合适，避免影响训练效率和稳定性。常见的激活函数包括阶跃函数（感知机所用，输入超0输出1，否则为0 ）、tanh函数（将输入映射到(-1, 1)区间）和ReLU函数（线性修正单元 ）。

多层感知机的学习与训练：神经网络的学习过程是在输入样本刺激下，动态调整连接权值和拓扑结构，使输出逼近期望结果，本质是对可变权值的调整。训练时，前向传播将输入样本从输入层经隐藏层传递到输出层，产生预测结果；反向传播则从输出层开始，将误差反向传播至各层，计算参数梯度并修正权值。

模型评估指标与数据集划分：训练误差衡量模型在训练数据集上的表现，泛化误差反映模型在新数据集上的性能。为计算这两种误差，需合理划分数据集。验证数据集用于评估模型好坏，通常选取部分训练数据，要避免与训练集混淆；测试数据集用于评估最终模型性能，理论上仅使用一次，如高考。在数据量不足时，K - 折交叉验证是有效的方法，将训练数据划分为K个部分，轮流使用其中一部分作为验证集，其余用于训练，最后报告K次验证的平均误差，常见K值为5或10。

过拟合与欠拟合及应对策略：

 

过拟合是模型过度学习训练样本的特点，将特殊情况当作普遍规律；欠拟合则是模型未能充分学习训练样本的一般性质。模型复杂度受参数个数和参数值选择范围影响，数据复杂度涉及样本数量、特征数量、时间和空间结构及多样性等因素。为应对过拟合，可采用权重衰减和暂退法（丢弃法）等策略。

总结

感知机作为神经网络的起点，虽功能有限，但为理解复杂模型奠定了基础。结合图像识别技术，需掌握从数据预处理到模型优化的全流程，并关注实际场景中的技术落地挑战（如计算资源、实时性要求）。