使用示例:
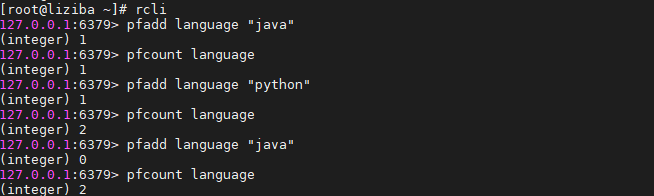
2.2 PFCOUNT key [key …]
PFCOUNT 指令后面可以跟多个key,当PFCOUNT key [key …]命令作用于单个键时,返回存储在给定键的HyperLogLog的近似基数,如果键不存在,则返回0;当PFCOUNT key [key …]命令作用于多个键时,返回所给定HyperLogLog的并集的近似基数,这个近似基数是通过将索引给定HyperLogLog合并至一个临时HyperLogLog来计算得出的。
返回值:
返回给定HyperLogLog包含的唯一元素的近似数量的整数值
时间复杂度:
当命令作用于单个HyperLogLog时,时间复杂度为O(1),并且具有非常低的平均常数时间。当命令作用于N个HyperLogLog时,时间复杂度为O(N),常数时间会比单个HyperLogLog要大的多。
使用示例:

2.3 PFMERGE destkey sourcekey [sourcekey …]
将多个HyperLogLog合并到一个HyperLogLog中,合并后HyperLogLog的基数接近于所有输入HyperLogLog的可见集合的并集,合并后得到的HyperLogLog会被存储在destkey键里面,如果该键不存在,那么命令在执行之前,会先为该键创建一个空的HyperLogLog。
返回值:
字符串回复,返回OK
时间复杂度:
O(N),其中N为被合并的HyperLogLog的数量,不过这个命令的常数复杂度比较高
使用示例:

三、原理
3.1 伯努利试验
HyperLogLog的算法设计能使用12k的内存来近似的统计2^64个数据,这个和伯努利试验有很大的关系,因此在探究HyperLogLog原理之前,需要先了解一下伯努利试验。
以下是百度百科关于伯努利试验的介绍:
伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努利概型。单个伯努利试验是没有多大意义的,然而,当我们反复进行伯努利试验,去观察这些试验有多少是成功的,多少是失败的,事情就变得有意义了,这些累计记录包含了很多潜在的非常有用的信息。
伯努利试验是数据概率论中的一部分,它的典故源于“抛硬币”。
**一个硬币只有正面和反面,每次抛硬币出现正反面的概率都是50%,我们一直抛硬币直到出现第一次正面为止,记录抛硬币的次数,这个就被称为一次伯努利试验。**伯努利试验需要做非常多的次数,数据才会变得有意义。
对于n次伯努利试验,出现正面的次数为n,假设每次伯努利试验抛掷的次数为k(也就是每次出现正面抛掷的次数),第一次伯努利试验抛掷次数为k1,第n次伯努利试验抛掷次数为kn,在这n次伯努利试验中,抛掷次数最大值为kmax。
上述的伯努利试验,结合极大似然估算方法(极大似然估计),得出n和kmax之间的估算关系:n=2^kmax。很显然这个估算关系是不准确的,例如如下案例:
第一次试验:抛掷1次出现正面,此时k=1,n=1;
第二次实验:抛掷3次出现正面,此时k=3,n=2;
第三次实验:抛掷6次出现正面,此时k=6,n=3;
第n次试验:抛掷10次出现正面,此时k=10,n=n,通过估算关系计算,n=2^10
上述案例可以看出,假设n=3,此时通过估算关系n=2kmax,26 ≠3,而且偏差很大。因此得出结论,这种估算方法误差很大。
3.2 估值优化
关于上述估值偏差较大的问题,可以采用如下方式结合来缩小误差:
-
增加测试的轮数,取平均值。假设三次伯努利试验为1轮测试,我们取出这一轮试验中最大的的kmax作为本轮测试的数据,同时我们将测试的轮数定位100轮,这样我们在100轮实验中,将会得到100个kmax,此时平均数就是(k_max_1 + … + k_max_m)/m,这里m为试验的轮数,此处为100.
-
增加修正因子,修正因子是一个不固定的值,会根据实际情况来进行值的调整。
上述这种增加试验轮数,去kmax的平均值的方法,是LogLog算法的实现。因此LogLog它的估算公式如下:
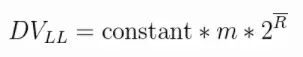
HyperLogLog与LogLog的区别在于HyperLogLog使用的是调和平均数,并非平均数。调和平均数指的是倒数的平均数(调和平均数)。调和平均数相比平均数能降低最大值对平均值的影响,这个就好比我和马爸爸两个人一起算平均工资,如果用平均值这么一下来我也是年薪数十亿,这样肯定是不合理的。
使用平均数和调和平均数计算方式如下:
假设我的工资20000,马云1000000000
使用平均数的计算方式:(20000 + 1000000000) / 2 = 500010000
调和平均数的计算方式:2/(1/20000 + 1/1000000000) ≈ 40000
很明显,平均工资月薪40000更加符合实际平均值,5个亿不现实。
调和平均数的基本计算公式如下:

3.3 HyperLogLog的实现
根据3.1和3.2大致可以知道HyperLogLog的实现原理了,它的主要精髓在于通过记录下低位连续零位的最大长度K(也就是上面我们说的kmax),来估算随机数的数量n。
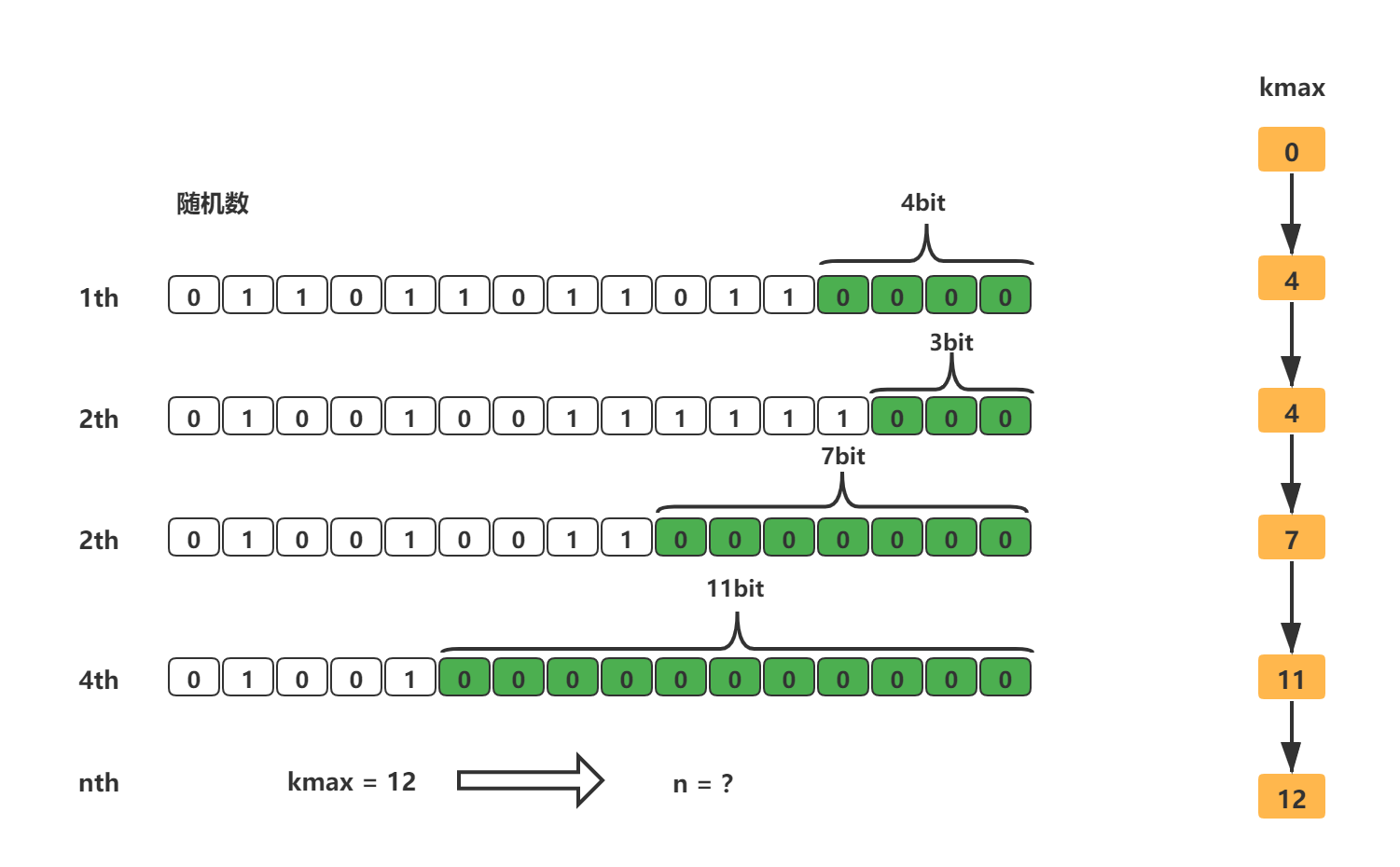
任何值在计算机中我们都可以将其转换为比特串,也就是0和1组成的bit数组,我们从这个bit串的低位开始计算,直到出现第一个1为止,这就好比上面的伯努利试验抛硬币,一直抛硬币直到出现第一个正面为止(只是这里是数字0和1,伯努利试验中使用的硬币的正与反,并没有区别)。而HyperLogLog估算的随机数的数量,比如我们统计的UV,就好比伯努利试验中试验的次数。
综上所述,HyperLogLog的实现主要分为三步:
第一步:转为比特串
通过hash函数,将输入的数据装换为比特串,比特串中的0和1可以类比为硬币的正与反,这是实现估值统计的第一步
第二步:分桶
分桶就是上面3.2估值优化中的分多轮,这样做的的好处可以使估值更加准确。在计算机中,分桶通过一个单位是bit,长度为L的大数组S,将数组S平均分为m组,m的值就是多少轮,每组所占有的比特个数是相同的,设为 P。得出如下关系:
-
L = S.length
-
L = m * p
-
数组S的内存 = L / 8 / 1024 (KB)
在HyperLogLog中,我们都知道它需要12KB的内存来做基数统计,原因就是HyperLogLog中m=16834,p=6,L=16834 * 6,因此内存为=16834 * 6 / 8 / 1024 = 12 (KB),这里为何是6位来存储kmax,因为6位可以存储的最大值为64,现在计算机都是64位或32位操作系统,因此6位最节省内存,又能满足需求。
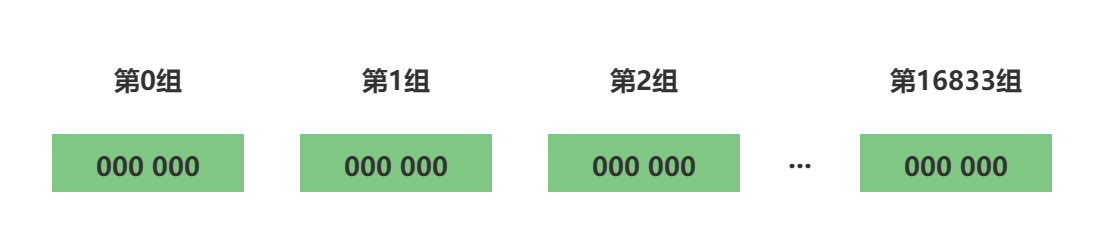
第三步:桶分配
最后就是不同的数据该如何分配桶,我们通过计算hash的方式得到比特串,只要hash函数足够好,就很难产生hash碰撞,我们假设不同的数值计算得到不同的hash值,相同的数值得到相同的hash值(这也是HyperLogLog能用来统计UV的一个关键点),此时我们需要计算值应该放到那个桶中,可以计算的方式很多,比如取值的低16位作为桶索引值,或者采用值取模的方式等等。
3.4 代码实现-BernoulliExperiment(伯努利试验)
首先来写一个3.1中伯努利试验n=2^kmax的估算值验证,这个估算值相对偏差会比较大,在试验轮次增加时估算值的偏差会有一定幅度的减小,其代码示例如下:
package com.lizba.pf;
import java.util.concurrent.ThreadLocalRandom;
/**
*
* 伯努利试验 中基数n与kmax之间的关系 n = 2^kmax
*
* @Author: Liziba
* @Date: 2021/8/17 23:16
*/
public class BernoulliExperimentTest {
static class BitKeeper {
/** 记录最大的低位0的长度 */
private int kmax;
public void random() {
// 生成随机数
long value = ThreadLocalRandom.current().nextLong(2L << 32);
int len = this.lowZerosMaxLength(value);
if (len > kmax) {
kmax = len;
}
}
/**
* 计算低位0的长度
* 这里如果不理解看下我的注释
* value >> i 表示将value右移i, 1<= i <32 , 低位会被移出
* value << i 表示将value左移i, 1<= i <32 , 低位补0
* 看似一左一右相互抵消,但是如果value低位是0右移被移出后,左移又补回来,这样是不会变的,但是如果移除的是1,补回的是0,那么value的值就会发生改变
* 综合上面的方法,就能比较巧妙的计算低位0的最大长度
* @param value
* @return
*/
private int lowZerosMaxLength(long value) {
int i = 1;
for (; i < 32; i++) {
if (value >> i << i != value) {
break;
}
}
return i - 1;
}
}
static class Experiment {
/** 测试次数n */
private int n;
private BitKeeper bitKeeper;
public Experiment(int n) {
this.n = n;
this.bitKeeper = new BitKeeper();
}
public void work() {
for(int i = 0; i < n; i++) {
this.bitKeeper.random();
}
}
/**
* 输出每一轮测试次数n
* 输出 logn / log2 = k 得 2^k = n,这里的k即我们估计的kmax
* 输出 kmax,低位最大0位长度值
*/
public void debug() {
System.out.printf(“%d %.2f %d\n”, this.n, Math.log(this.n) / Math.log(2), this.bitKeeper.kmax);
}
}
public static void main(String[] args) {
for (int i = 0; i < 100000; i++) {
Experiment experiment = new Experiment(i);
experiment.work();
experiment.debug();
}
}
}
我们可以通过修改main函数中,测试的轮次,再根据输出的结果来观察,n=2^kmax这样的结果还是比较吻合的。
3.5 代码实现-HyperLogLog
接下来根据HyperLogLog中采用调和平均数+分桶的方式来做代码优化,模拟简单版本的HyperLogLog算法的实现,其代码如下:
package com.lizba.pf;
import java.util.concurrent.ThreadLocalRandom;
/**
*
* HyperLogLog 简单实现
*
* @Author: Liziba
* @Date: 2021/8/18 10:40
*/
public class HyperLogLogTest {
static class BitKeeper {
/** 记录最大的低位0的长度 */
private int kmax;
/**
* 计算低位0的长度,并且保存最大值kmax
* @param value
*/
public void random(long value) {
int len = this.lowZerosMaxLength(value);
if (len > kmax) {
kmax = len;
}
}
/**
* 计算低位0的长度
* 这里如果不理解看下我的注释
* value >> i 表示将value右移i, 1<= i <32 , 低位会被移出
* value << i 表示将value左移i, 1<= i <32 , 低位补0
* 看似一左一右相互抵消,但是如果value低位是0右移被移出后,左移又补回来,这样是不会变的,但是如果移除的是1,补回的是0,那么value的值就会发生改变
* 综合上面的方法,就能比较巧妙的计算低位0的最大长度
* @param value
* @return
*/
private int lowZerosMaxLength(long value) {
int i = 1;
for (; i < 32; i++) {
if (value >> i << i != value) {
break;
}
}
return i - 1;
}
}
static class Experiment {
private int n;
private int k;
/** 分桶,默认1024,HyperLogLog中是16384个桶,并不适合我这里粗糙的算法 */
private BitKeeper[] keepers;
public Experiment(int n) {
this(n, 1024);
}
public Experiment(int n, int k) {
this.n = n;
this.k = k;
this.keepers = new BitKeeper[k];
for (int i = 0; i < k; i++) {
this.keepers[i] = new BitKeeper();
}
}
/**
* (int) (((m & 0xfff0000) >> 16) % keepers.length) -> 计算当前m在keepers数组中的索引下标
* 0xfff0000 是一个二进制低16位全为0的16进制数,它的二进制数为 -> 1111111111110000000000000000
* m & 0xfff0000 可以保理m高16位, (m & 0xfff0000) >> 16 然后右移16位,这样可以去除低16位,使用高16位代替高16位
* ((m & 0xfff0000) >> 16) % keepers.length 最后取模keepers.length,就可以得到m在keepers数组中的索引
*/
public void work() {
for (int i = 0; i < this.n; i++) {
long m = ThreadLocalRandom.current().nextLong(1L << 32);
BitKeeper keeper = keepers[(int) (((m & 0xfff0000) >> 16) % keepers.length)];
keeper.random(m);
}
}
/**
* 估算 ,求倒数的平均数,调和平均数
* @return
*/
public double estimate() {
double sumBitsInverse = 0.0;
// 求调和平均数
for (BitKeeper keeper : keepers) {
sumBitsInverse += 1.0 / (float) keeper.kmax;
}
double avgBits = (float) keepers.length / sumBitsInverse;
return Math.pow(2, avgBits) * this.k;
}
}
/**
* 测试
* @param args
*/
public static void main(String[] args) {
for (int i = 100000; i < 1000000; i+=100000) {
Experiment experiment = new Experiment(i);
experiment.work();
double estimate = experiment.estimate();
// i 测试数据
// estimate 估算数据
// Math.abs(estimate - i) / i 偏差百分比
System.out.printf(“%d %.2f %.2f\n”, i, estimate, Math.abs(estimate - i) / i);























 3027
3027

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








