基于层次分析法赋权的TOPSIS法

据相关媒体报道，2023 年考研可以称得上是“最难”的一年，全国研究生报考人数突破新高达到 474 万人部分考研学生感染新冠带病赴考、保研名额增多挤压考研录取名额等因素都导致了 2023 年考研上岸难度加大。不少同学参加完 2023 年考研直呼：今年考研也太难了！从客观的角度来说，2023 年考研确实不简单，考研难度甚至超过了之前的任何一年。报考人数突破新高，保研率持续上涨，录取率降低。不少 985 高校保研率都已经突破了 50%，考取 985 高校的考生竞争非常激烈，录取的可能进一步降低。从数据来看，2023 年考研上岸的难度比往年更大。根据不完全统计，2023年考研录取率将低于 20%，将有超过 300 万考生落榜。基于以上背景，请你们的团队收集相关数据，研究解决以下问题：

 

问题 1. 量化分析 2023 年考研有多难，导致考研难的主要因素有哪些？

模型假设与理由：

假设一：数据来源来源与数据质量有所保证

理由：由于考研数据来源渠道多样与个渠道信息杂糅的原因，我们只采用官方给出的数据，并采用专家打分的方式去计算各个指标的权重

假设二：忽略天气、疫情等因素的影响

理由：在2023年，疫情等客观因素的确为考研造成了极大的困扰，但这些数据由于难以统计和量化的问题不被我们考虑在内，忽略这些因素也提高了模型的普适性

5.1问题1：量化2023年考研有多难，导致2023年考研难的因素主要有哪些？

关于此问题我们建立基于层次分析法赋权的TOPSIS模型

5.1.1 搜集数据并进行预处理

从官方网站搜集了2023-2021年研究生录取人数、报考人数等相关数据，绘制出下表

	报考人数	录取率	保研公示人数	A类平均考研成绩查询
2023年	474万	24.23%	15.5万	315.77
2022年	457万	24.15%	14万	320.46
2021年	377万	27.87%	12.26万	310.46

因为这里既有极大型指标又有极小型指标，所以我们这里要先进行指标正向化。TOPSIS优劣解距离法，根据层次分析法计算得出的权重，进一步计算综合得分指数，衡量2023 年度考研难度。TOPSIS 法是 C.L.Hwang 和 K.Yoon 于 1981 年首次提出，根据有限个评价对象与理想化目标的接近程度进行排序。

 

指标名称	指标特点
极大型（效益型）指标	越大（越多）越好
极小型（成本型）指标	越小（越少）越好
中间型指标	越接近某个值越好
区间型指标	落在某个区间内最好

因此我们先对数据进行正向化处理，正向化处理就是把不同的指标类型都转化为极大型指标

X=Xmax-X

为消除不同指标量纲的影响，我们还有必要对已经正向化的指标进行标准化处理，为保证标准化后各项指标仍为正值，我们不采用一般概率统计当中

的标准化思路，记标准化后的矩阵为Z，其中Zij=

，也就是

对数据进行了相应的处理后，可以用Zi来表达第 i 个方案。假设有 n 个待评价的方案，m 个指标，此时Zi=[Zi1,Zi2,..,Zim]由这m个数据构成的矩阵也就是我们的标准化矩阵了：

 

 

5.1.2层次分析法赋权

因为要利用层次分析法对各项指标进行赋权，因此我们先制作调查问卷，采用专家打分的方式并搜集调查问卷，最后绘制出判断矩阵如下：

	报考人数	录取率	保研公示人数	A类平均考研成绩查询
报考人数	1	1/9	1/7	1/6
录取率	9	1	3	2
保研公示人数	7	1/3	1	1/2
A类平均考研成绩查询	6	1/2	2	1

根据层次分析法，我们先要计算一致性指标：

其中，n为矩阵的最大阶数，λmax为矩阵的最大特征值，进而计算一致性比例。

当

CR < 0.1

我们认为判断矩阵的一致性检验可以接受

经计算，该判断矩阵的一致性指标和一致性比例分别为

CI = 0.0856913107, CR =  0.0952125 < 0.1

因此，该判断矩阵是可以接受的。

利用算数平均法并归一化求得权重：

R = [ 0.0694, 0.4893,0.2217,0.2197]

5.1.3 赋权TOPSIS法来量化2023年考研难度：

经过了正向化处理和标准化处理并加权的评分矩阵 Z，里面的数据全部是极大型数据。我们就可以从中取出理想最优解和最劣解。取出每个指标，即每一列中最大的数，构成理想最优解向量，即：

 

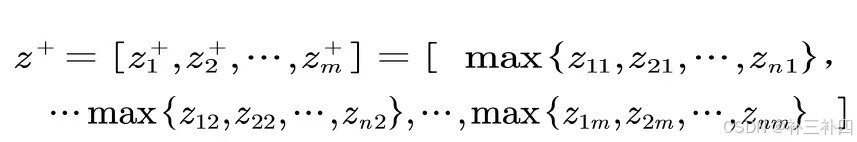
同理，取出每一列的最劣解向量：

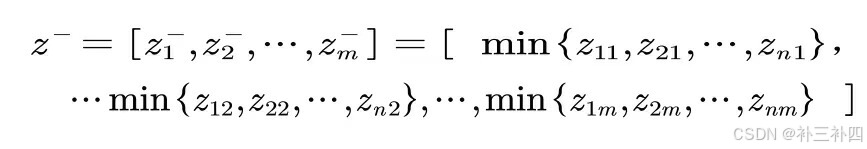
对于第i个方案 ，我们计算它与最优解的距离：

与最劣解的距离：

定义第i个方案的评分Si：

最终我们得到2023年考研难度在TOPSIS法下2023年的相对接近度就是其分数：

2023年的相对接近度（分数）: 0.6411341053712002

综上所述2023年考研难度达0.641分，导致2023年考研难的主要因素有保研率的提高、报考人数的增加、考研分数的上涨、逆向考研的现象上涨、录取率的下降以及疫情方面的影响。

附录：

import numpy as np



# 输入四维判断矩阵

A = np.array([[1, 1/7, 1/2, 1/5],

              [7, 1, 3, 2],

              [2, 1/3, 1, 2],

              [5, 1/2, 1/2, 1]])



# 使用算术平均法求权重

# 计算每一列的和

column_sums = np.sum(A, axis=0)



# 计算每个元素占其所在列的比例

proportions = A / column_sums



# 计算每个元素所在行的比例的平均值，即为权重

weights = np.mean(proportions, axis=1)



# 归一化权重，使其和为1

weights = weights / np.sum(weights)



print("算术平均法求得的权重：", weights)



# 计算判断矩阵的最大特征值和对应的特征向量

eigenvalues, eigenvectors = np.linalg.eig(A)

max_eigenvalue = np.max(np.real(eigenvalues))

max_eigenvector = np.real(eigenvectors[:, np.argmax(eigenvalues)])



# 计算一致性指标CI

n = A.shape[0]

CI = (max_eigenvalue - n) / (n - 1)



# 查表得到平均随机一致性指数RI，并精确到小数点后两位

RI_dict = {1: 0.00, 2: 0.00, 3: 0.58, 4: 0.90, 5: 1.12, 6: 1.24, 7: 1.32, 8: 1.41, 9: 1.45}

RI = RI_dict[n]



# 计算一致性比率CR

CR = CI / RI if RI != 0 else 0



print("最大特征值：", max_eigenvalue)

print("最大特征向量：", max_eigenvector)

print("一致性指标CI：", CI)

print("平均随机一致性指数RI：", RI)

print("一致性比率CR：", CR)



if CR < 0.1:

    print("判断矩阵通过一致性检验")

else:

print("判断矩阵未通过一致性检验")

import numpy as np



# 创建矩阵（去掉年份列）

data_matrix = np.array([

    [114.84, 0.2423, 15.5, 315.77],

    [110.35, 0.2415, 14.0, 320.46],

    [105.07, 0.2787, 12.26, 310.46]

])



# 找到录取率的最大值

max_admission_rate = np.max(data_matrix[:, 1])

print("录取率的最大值:", max_admission_rate)



# 对录取率进行正向化处理 (max - x)

data_matrix[:, 1] = max_admission_rate - data_matrix[:, 1]

print("正向化处理后的矩阵:")

print(data_matrix)



# 计算正向化处理后的录取率的标准差

admission_rate_std = np.std(data_matrix[:, 1])

print("正向化处理后录取率的标准差:", admission_rate_std)



# 标准化：对每一列元素除以该列的平方和的平方根

data_matrix = data_matrix / np.sqrt(column_sums_of_squares)

print("标准化处理后的矩阵:")

print(data_matrix)





# 赋权

weights = np.array([0.0694, 0.4893, 0.2217, 0.2197])

weighted_matrix = data_matrix * weights

print("赋权后的矩阵:")

print(weighted_matrix)



# 计算正理想解和负理想解

positive_ideal_solution = np.max(weighted_matrix, axis=0)

negative_ideal_solution = np.min(weighted_matrix, axis=0)

print("正理想解:", positive_ideal_solution)

print("负理想解:", negative_ideal_solution)



# 计算2023年与正理想解和负理想解的距离

distance_to_positive_ideal_2023 = np.linalg.norm(weighted_matrix[0, :] - positive_ideal_solution)

distance_to_negative_ideal_2023 = np.linalg.norm(weighted_matrix[0, :] - negative_ideal_solution)

print("2023年到正理想解的距离:", distance_to_positive_ideal_2023)

print("2023年到负理想解的距离:", distance_to_negative_ideal_2023)



# 计算2023年的相对接近度

relative_closeness_2023 = distance_to_negative_ideal_2023 / (distance_to_positive_ideal_2023 + distance_to_negative_ideal_2023)

print("2023年的相对接近度（分数）:", relative_closeness_2023)