对称密码（DES）

已于 2024-12-03 01:02:52 修改
阅读量379 收藏 1
点赞数 1
文章标签： 密码学 算法
于 2024-11-05 17:22:13 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/2401_88324198/article/details/143511649
版权

一、比特序列（0和1排列而成）运算

1.编码（≠加密）过程

明文字母→ASCII(十进制)→二进制

二、XOR运算（异或）

1.一个比特的异或

0 XOR 0 = 0

1 XOR 0 = 1

0 XOR 1 = 1

1 XOR 1 = 0

2.多个比特的异或（一一对应）

0 1 0 1 0 1 0 1 0 1

         XOR

0 1 0 1 0 1 1 0 1 0

             = 

0 0 0 0 0 0 1 1 1 1

3.不可推测的蒙版中的比特序列是随机数

三、DES

1.加密和解密

将64比特的明文加密成64比特的密文，规格上来所密钥长度是64比特，但是每隔7个比特会有一个比特用来校验,校验位为8，16，24，32，40，48，56，64，因此实际上密钥只有56比特。

64比特的单位称为分组。

迭代加密称为模式。

2.结构（Feistel网络）

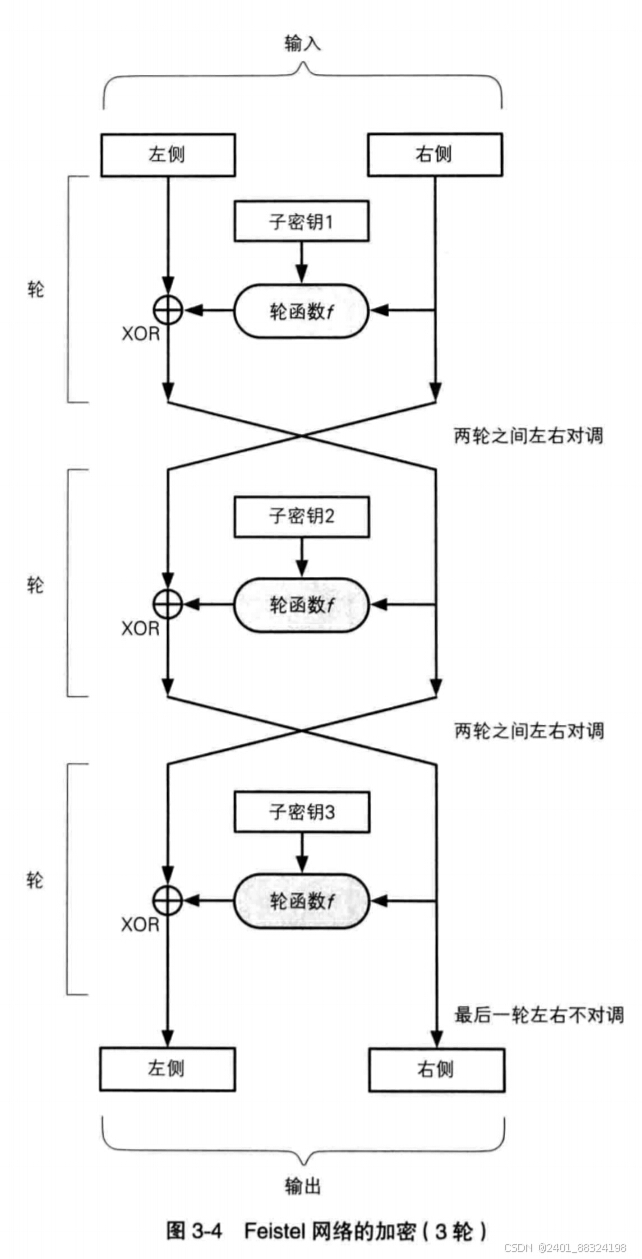
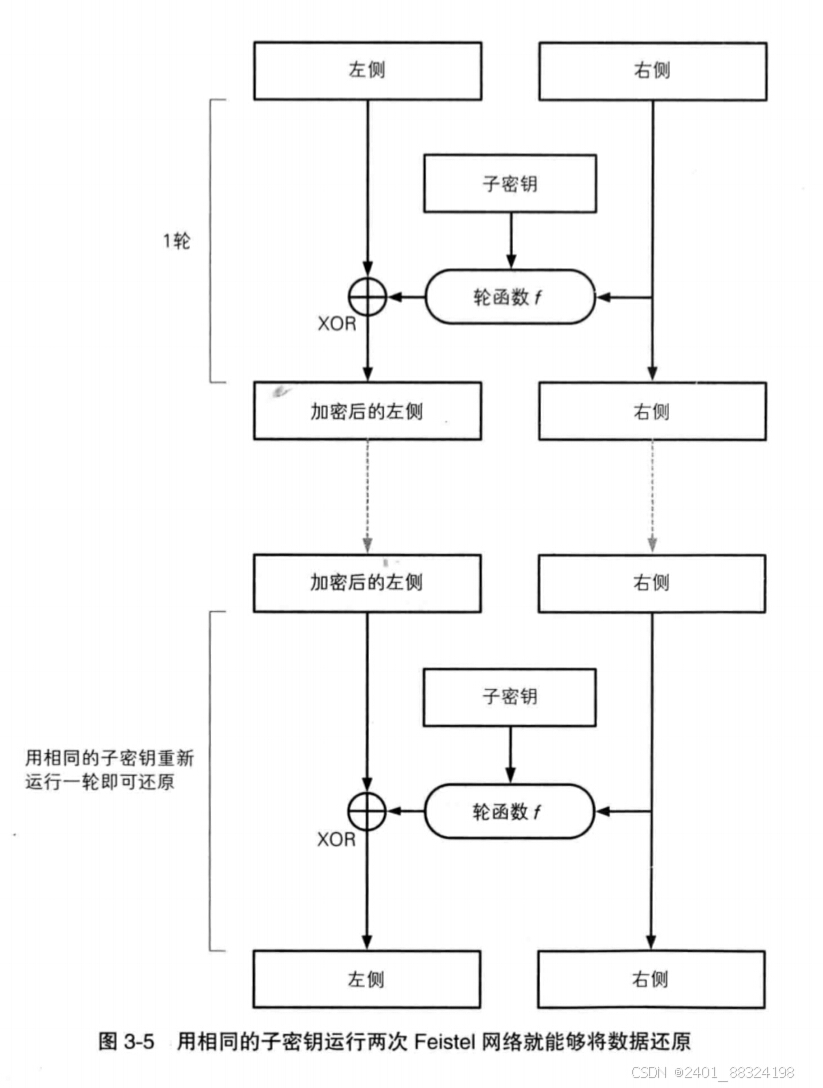
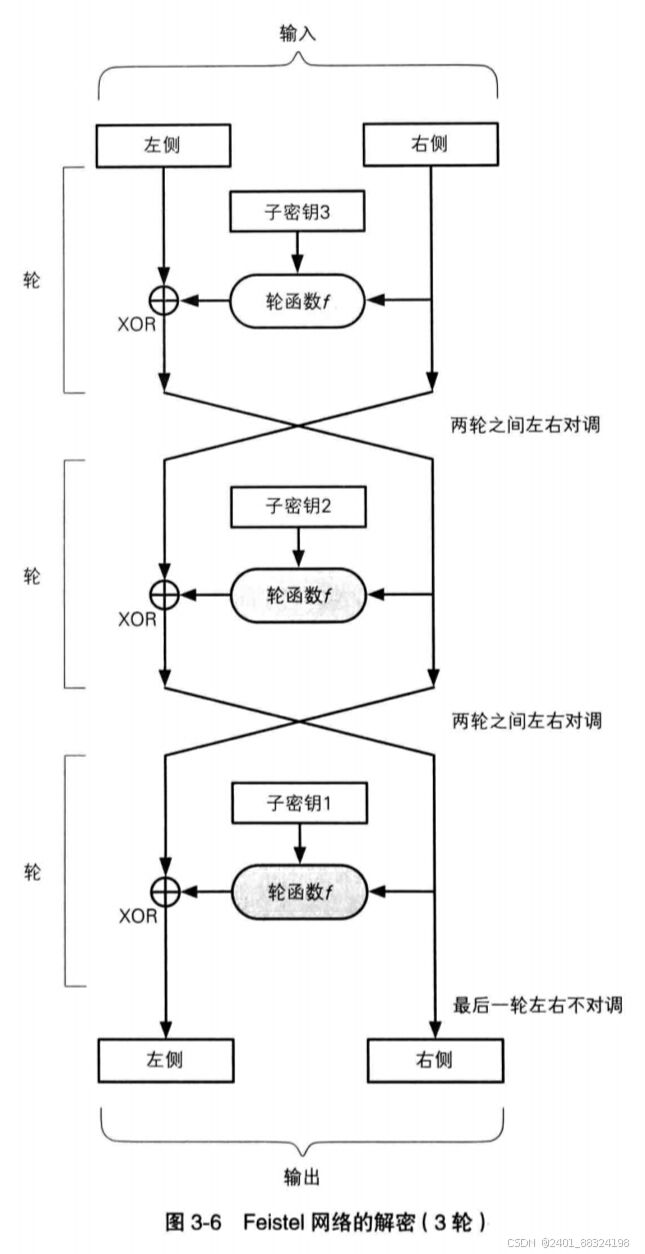
3.具体算法http://【金山文档 | WPS云文档】 DES加密算法 https://kdocs.cn/l/ci9U9bGrd8FX

DES

基本原理

  1. DES算法是一个分组加密的对称密码算法。

  2. 密钥长64位,56位参与运算,其余8位为校验位。(8,16,24,32,40,48,56,64)

  3. 当n个64位明文数据块都经过DES加密处理后,所得到的n个64位密文数据块串在一起就是密文。

明文IP置换

先将明文换成二进制

#转化为二进制数的代码解释
plain = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in plain])
'''
for i in plain: 对于 plain 列表中的每个元素 i 进行迭代。
bin(i): 将整数 i 转换为二进制字符串。
[2:]: 去除二进制字符串中的前缀 "0b"。
zfill(8): 在二进制字符串的左侧填充零，使其总长度为 8。
list(map(int, ...)): 将二进制字符串中的每个字符转换为整数，并将结果放入一个列表。
[...] for i in plain: 将步骤 5 中的结果放入一个列表，形成一个二维列表。
reduce(add, ...): 使用 reduce 函数和 add 函数对步骤 6 中的二维列表进行累加，将所有的二进制位连接成一个大的二进制列表。
'''

按照⼀定的规则，将原来的64位⼆进制明文重新排序。

_IP = [57, 49, 41, 33, 25, 17, 9,  1,
    59, 51, 43, 35, 27, 19, 11, 3,
    61, 53, 45, 37, 29, 21, 13, 5,
    63, 55, 47, 39, 31, 23, 15, 7,
    56, 48, 40, 32, 24, 16, 8,  0,
    58, 50, 42, 34, 26, 18, 10, 2,
    60, 52, 44, 36, 28, 20, 12, 4,
    62, 54, 46, 38, 30, 22, 14, 6
]
​
def IP(plain: List[int]):
    return list(map(lambda x: plain[x], _IP))
'''
lambda x: plain[x]是一个匿名函数，它接受一个参数x，并返回plain[x]的值。在这里，x表示_IP列表中的索引值，plain[x]表示根据索引值从plain列表中获取对应的元素。
​
map(lambda x: plain[x], _IP)的作用是将_IP列表中的每个元素作为索引值，通过匿名函数映射到plain列表中的对应元素，最终返回一个映射后的结果列表。
     plain = b'12345678'
     plain = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in plain])
'''
64位均分为两组，一组32位，即为L。和R。。

block = IP(plain)
L, R = block[:32], block[32:]  #切片操作
'''
调用IP函数，将置换后的明文plain赋值给block
再将block分为L R 两部分
[:32]可以返回该列表从开头到第 31 个元素（索引为 0 开始计数，所以是到索引为 31 的元素）组成的新列表
'''

轮函数——E扩展置换

将R的32位输⼊扩展为48位输出。

#E扩展表
__expansion_table = [
    31,  0,  1,  2,  3,  4,
     3,  4,  5,  6,  7,  8,
     7,  8,  9, 10, 11, 12,
    11, 12, 13, 14, 15, 16,
    15, 16, 17, 18, 19, 20,
    19, 20, 21, 22, 23, 24,
    23, 24, 25, 26, 27, 28,
    27, 28, 29, 30, 31,  0
]
​
def EP(data: List[int]):  # 扩展置换
    return list(map(lambda x: data[x], __expansion_table)) #x表示_EP列表中的索引值

轮函数——S盒压缩处理

经过扩展的48位明⽂和48位密钥进⾏异或运算。

   R = EP(R)  # 扩展置换
   R = list(map(lambda x, y: x ^ y, R, skeys[index])) 
    # 异或
'''
map(lambda x, y: x ^ y, R, skeys[index]) 
首先，map() 函数在这里被用来对两个序列中的对应元素应用一个匿名函数 lambda x, y: x ^ y。
这里的 x 来自于经过扩展置换后的 R，
y 来自于 skeys[index]     (假设 skeys 是一个列表 [10, 20, 30, 40, 50]，如果 index 的值为 2，那么 skeys[index] 就会返回 30)。
匿名函数 lambda x, y: x ^ y 的作用是对传入的两个参数 x 和 y 进行按位异或操作。所以这行代码整体上就是对 R 和 skeys[index] 这两个序列的对应元素逐一进行按位异或操作，然后将得到的结果组成一个新的序列（通过 list() 函数将 map() 函数返回的可迭代对象转换为列表），并重新赋值给 R。
'''
​
'''
相关密钥生成函数
def get_sub_key(key: List[int]):
    key = PC_1(key) # PC-1置换
    L, R = key[:28], key[28:] # 分成两半
​
    skeys = []
​
    for i in range(16):
        for j in range(ROTATIONS[i]): # 根据轮次左移
            L = L[1:] + L[:1]  #将 L 原来的第一个元素移到了序列的末尾。
            R = R[1:] + R[:1]
​
        skeys.append(PC_2(L+R)) # PC-2置换
    
    return skeys
'''

将48位输⼊等分为8块，每块6位输⼊压缩为4位输出，得到32 位数据。

#将48位输入等分为8块，每块6位输入压缩为4位输出
def F(index: int, R: List[int], skeys: List[List[int]]):
    """
    index: 代表这是第几轮
    R: 输入数据
    skeys: 子密钥数组
    """
    R = EP(R)  # 扩展置换
    R = list(map(lambda x, y: x ^ y, R, skeys[index]))  # 异或
    B = [R[:6], R[6:12], R[12:18], R[18:24], R[24:30], R[30:36], R[36:42], R[42:]]  # 分成八份
​
Bn = [0] * 32  #创建一个新的列表 Bn，并将其初始化为包含 32 个元素，且每个元素的值都为 0。这个列表将在后续基于 S 盒的处理中用于存储中间结果。
pos = 0  #定义一个变量 pos（通常可以理解为 “位置”“指针” 等含义记录位置），并将其初始值赋为 0。
for i in range(8):  #8次s盒循环
    
    #  计算该使用S盒的行坐标和列坐标
    row = (B[i][0] << 1) + B[i][5] #组合六位的首末位
    #首先根据 B 列表中第 i 个子部分（即 B[i]）的第一个元素 B[i][0] 和第六个元素 B[i][5]来计算用于 S 盒操作的行坐标。（计算格式：假如假设 B[i][0] 的值为整数 1，1 的二进制表示为 1。当进行 B[i][0] << 1 操作时，将其二进制位向左移动 1 位，得到 10，也就是十进制的 2，再加上B[i][5]=1，十进制依然是1，则row=3）
    '左移操作原理'
        '当对一个整数进行左移操作时，它在二进制表示下，所有的位都向左移动指定的位数（这里是 1 位），右边空出的位用 0 填充。
        
    col = (B[i][1] << 3) + (B[i][2] << 2) + (B[i][3] << 1) + B[i][4]  #组合中间四位形成新的二进制
​
    sb = __sbox[i][(row << 4) + col]  #sb是s盒中的十进制数字
​
    Bn[pos + 0] = (sb & 8) >> 3  # 四位输出，首先 sb & 8 是进行按位与操作，它会将 sb 中的每一位与二进制数 1000（十进制的 8）进行按位与运算，这样做的结果是只会保留 sb 中对应二进制位为 1 的那些位
    Bn[pos + 1] = (sb & 4) >> 2
    Bn[pos + 2] = (sb & 2) >> 1
    Bn[pos + 3] = (sb & 1)
'与：是一种二进制位运算
    pos += 4
R = P(Bn)
return R

第3行第15列是13，转化为二进制就是1101，这样进行8次，得到32位密文。

P盒置换

S盒位再经过P盒置换。⾄此，⼀次轮函数操作完毕。

__p = [
    15, 6, 19, 20, 28, 11,
    27, 16, 0, 14, 22, 25,
    4, 17, 30, 9, 1, 7,
    23,13, 31, 26, 2, 8,
    18, 12, 29, 5, 21, 10,
    3, 24
]#P置换表
​
def P(data: List[int]):  # P置换
    return list(map(lambda x: data[x], __p))

与L0进行异或，并将值赋给R1

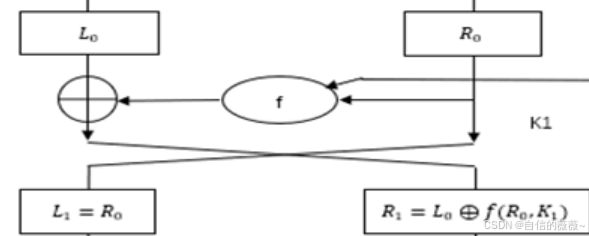
for i in range(16):
    tpR = R[:]#将R的值存给tpR
    R = F(i, R, skeys)
    R = list(map(lambda x, y: x ^ y, R, L))#将加密后的数与L进行异或并存给R
    L = tpR#将tcR的值赋给L，即交换R和L

IP逆置换

#逆置换表
_FP = [
	39,  7, 47, 15, 55, 23, 63, 31,
	38,  6, 46, 14, 54, 22, 62, 30,
	37,  5, 45, 13, 53, 21, 61, 29,
	36,  4, 44, 12, 52, 20, 60, 28,
	35,  3, 43, 11, 51, 19, 59, 27,
	34,  2, 42, 10, 50, 18, 58, 26,
	33,  1, 41,  9, 49, 17, 57, 25,
	32,  0, 40,  8, 48, 16, 56, 24
]

def FP(plain: List[int]):
    return list(map(lambda x: plain[x], _FP))

密钥生成

#其他代码中的
//轮密钥产生
void produceKey(char key[8],char keyL[16][48])
{
	char bit[64],keyout[56],C[28],D[28],temp[64];
	char8Tobit64(key,bit);
	//补8位奇偶校验位
	for(uchar j=0;j<8;j++)
	{
		memcpy(temp+j*8,bit+j*7,7);
		temp[j*8+7]=1;
	}
	memcpy(bit,temp,64);
	//64--->56
	reversePC_1(bit,keyout);
	memcpy(C,keyout,28);
	memcpy(D,keyout+28,28);
	for(uchar i=0;i<16;i++)
	{
		leftMove(C,D,Left_Move[i]);
		reversePC_2(C,D,keyL[i]);
	}
}

密钥为64位，进行PC-1置换除去8位校验位，剩余56位参与运算。

#首先据表PC-1进行置换
__pc1 = [56, 48, 40, 32, 24, 16,  8,
	  0, 57, 49, 41, 33, 25, 17,
	  9,  1, 58, 50, 42, 34, 26,
	 18, 10,  2, 59, 51, 43, 35,
	 62, 54, 46, 38, 30, 22, 14,
	  6, 61, 53, 45, 37, 29, 21,
	 13,  5, 60, 52, 44, 36, 28,
	 20, 12,  4, 27, 19, 11,  3
]#密钥置换表1
def get_sub_key(key: List[int]):
    key = PC_1(key) # PC-1置换

56位的密钥分成两组分别为28位，C。=1111000 0110011 0010101 0101111

和D。=0101010 1011001 1001111 0001111。

#分为c1,c2
 L, R = key[:28], key[28:] # 分成两半

根据移位次数表进行循环左移得到C1和D1~C16和D16。

C1=1110000 1100110 0101010 1011111

D1=1010101 0110011 0011110 0011110

#循环左移
ROTATIONS = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]#左移表
 for i in range(16):
        for j in range(ROTATIONS[i]): # 根据轮次左移
            L = L[1:] + L[:1]
            R = R[1:] + R[:1]
#L[1:]：这会获取列表 L 中除了第一个元素之外的所有元素，组成一个新的列表。例如，如果 L = [1, 2, 3, 4]，那么 L[1:] = [2, 3, 4]。    L[:1]：这会获取列表 L 中仅第一个元素，组成一个新的列表。例如，对于 L = [1, 2, 3, 4]，L[:1] = [1]。    L[1:] + L[:1]：将前面得到的两个新列表进行拼接，得到的结果就是将原列表 L 的第一个元素移到了末尾，实现了循环左移一位的效果。例如，对于 L = [1, 2, 3, 4]，经过 L[1:] + L[:1] 操作后，新的 L 变为 [2, 3, 4, 1]。

 '''
 代码包含两个嵌套的循环，外部循环迭代 16 次，内部循环迭代的次数由 ROTATIONS[i] 指定。
在每次内部循环中，L（左半部分）和 R（右半部分）分别执行了循环左移操作。
循环左移是指将二进制序列的位按照规定的位数向左移动，并将被移出的位重新放入序列的末尾。
 '''

拼接C1和D1。再进行PC-2,48位参与PC-2运算，得到K1。

__pc2 = [
    13, 16, 10, 23, 0, 4,
    2, 27, 14, 5, 20, 9,
    22, 18, 11, 3, 25, 7,
    15, 6, 26, 19, 12, 1,
    40, 51, 30, 36, 46, 54,
    29, 39, 50, 44, 32, 47,
    43, 48, 38, 55, 33, 52,
    45, 41, 49, 35, 28, 31
]

def PC_2(key: List[int]):
    return list(map(lambda x: key[x], __pc2))

按照交换规则，⽣成16个48位的轮密钥：K1~K16。

结束。

from operator import add
from typing import List
from functools import reduce

_IP = [57, 49, 41, 33, 25, 17, 9, 1,
       59, 51, 43, 35, 27, 19, 11, 3,
       61, 53, 45, 37, 29, 21, 13, 5,
       63, 55, 47, 39, 31, 23, 15, 7,
       56, 48, 40, 32, 24, 16, 8, 0,
       58, 50, 42, 34, 26, 18, 10, 2,
       60, 52, 44, 36, 28, 20, 12, 4,
       62, 54, 46, 38, 30, 22, 14, 6
       ]


def IP(plain: List[int]):  #根据_IP置换表对输入的明文列表进行初始置换操作，返回置换后的列表。

    return list(map(lambda x: plain[x], _IP)) #通过map函数和 lambda 表达式，按照_IP表中的索引从输入的明文中取出对应元素，组成新的列表。


__pc1 = [56, 48, 40, 32, 24, 16, 8,
         0, 57, 49, 41, 33, 25, 17,
         9, 1, 58, 50, 42, 34, 26,
         18, 10, 2, 59, 51, 43, 35,
         62, 54, 46, 38, 30, 22, 14,
         6, 61, 53, 45, 37, 29, 21,
         13, 5, 60, 52, 44, 36, 28,
         20, 12, 4, 27, 19, 11, 3
         ]

__pc2 = [
    13, 16, 10, 23, 0, 4,
    2, 27, 14, 5, 20, 9,
    22, 18, 11, 3, 25, 7,
    15, 6, 26, 19, 12, 1,
    40, 51, 30, 36, 46, 54,
    29, 39, 50, 44, 32, 47,
    43, 48, 38, 55, 33, 52,
    45, 41, 49, 35, 28, 31
]
ROTATIONS = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]  #一个列表，指定了在生成子密钥过程中每一轮的左移位数。


def PC_1(key: List[int]):
    return list(map(lambda x: key[x], __pc1))


def PC_2(key: List[int]):
    return list(map(lambda x: key[x], __pc2))


def get_sub_key(key: List[int]): #生成用于加密过程的子密钥列表。首先对密钥进行 PC-1 置换，然后将其分成左右两部分，根据ROTATIONS列表指定的轮次进行左移操作，最后通过 PC-2 置换得到每一轮的子密钥并添加到列表中返回。
    key = PC_1(key)  # PC-1置换
    L, R = key[:28], key[28:]  # 分成两半

    skeys = []

    for i in range(16):
        for j in range(ROTATIONS[i]):  # 根据轮次左移
            L = L[1:] + L[:1]
            R = R[1:] + R[:1]

        skeys.append(PC_2(L + R))  # PC-2置换

    return skeys


__expansion_table = [
    31, 0, 1, 2, 3, 4,
    3, 4, 5, 6, 7, 8,
    7, 8, 9, 10, 11, 12,
    11, 12, 13, 14, 15, 16,
    15, 16, 17, 18, 19, 20,
    19, 20, 21, 22, 23, 24,
    23, 24, 25, 26, 27, 28,
    27, 28, 29, 30, 31, 0
]  #扩展置换表，用于扩展数据以便后续与子密钥进行异或操作。
__sbox = [
    # S1
    [14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
     0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
     4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
     15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],

    # S2
    [15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
     3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
     0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
     13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],

    # S3
    [10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
     13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
     13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
     1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],

    # S4
    [7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
     13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
     10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
     3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],

    # S5
    [2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
     14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
     4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
     11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],

    # S6
    [12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
     10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
     9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
     4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],

    # S7
    [4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
     13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
     1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
     6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],

    # S8
    [13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
     1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
     7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
     2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
]
__p = [
    15, 6, 19, 20, 28, 11,
    27, 16, 0, 14, 22, 25,
    4, 17, 30, 9, 1, 7,
    23, 13, 31, 26, 2, 8,
    18, 12, 29, 5, 21, 10,
    3, 24
]


def EP(data: List[int]):  # 扩展置换
    return list(map(lambda x: data[x], __expansion_table))


def P(data: List[int]):  # P置换
    return list(map(lambda x: data[x], __p))


def F(index: int, R: List[int], skeys: List[List[int]]):
    """
    index: 代表这是第几轮
    R: 输入数据
    skeys: 子密钥数组
    """
    R = EP(R)  # 扩展置换
    R = list(map(lambda x, y: x ^ y, R, skeys[index]))  # 异或

    B = [R[:6], R[6:12], R[12:18], R[18:24], R[24:30], R[30:36], R[36:42], R[42:]]  # 分成八份

    Bn = [0] * 32
    pos = 0
    for i in range(8):
        #  计算该使用S盒的行坐标和列坐标
        row = (B[i][0] << 1) + B[i][5]
        col = (B[i][1] << 3) + (B[i][2] << 2) + (B[i][3] << 1) + B[i][4]

        sb = __sbox[i][(row << 4) + col]

        Bn[pos + 0] = (sb & 8) >> 3  # 四位输出
        Bn[pos + 1] = (sb & 4) >> 2
        Bn[pos + 2] = (sb & 2) >> 1
        Bn[pos + 3] = (sb & 1)

        pos += 4
    R = P(Bn)
    return R


_FP = [
    39, 7, 47, 15, 55, 23, 63, 31,
    38, 6, 46, 14, 54, 22, 62, 30,
    37, 5, 45, 13, 53, 21, 61, 29,
    36, 4, 44, 12, 52, 20, 60, 28,
    35, 3, 43, 11, 51, 19, 59, 27,
    34, 2, 42, 10, 50, 18, 58, 26,
    33, 1, 41, 9, 49, 17, 57, 25,
    32, 0, 40, 8, 48, 16, 56, 24
]


def FP(plain: List[int]):
    return list(map(lambda x: plain[x], _FP))


key = b'12345678'
plain = b'12345678'

# 转为二进制数组
key = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in key])
plain = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in plain])
skeys = get_sub_key(key)

block = IP(plain)

L, R = block[:32], block[32:]
for i in range(16):
    tpR = R[:]
    R = F(i, R, skeys)
    R = list(map(lambda x, y: x ^ y, R, L))
    L = tpR
block = R + L
block = FP(block)
enc = bytes([int(''.join(map(str, block[i * 8:(i + 1) * 8])), 2) for i in range(8)])

print(enc)

四、三重DES（3DES）

1.加密流程

加密→解密→加密

2.解密流程

解密→加密→解密

DES算法-S盒计算
qq_62940532的博客
05-30 1801
S2对应第一位和倒数第一位组成的二进制数为00，对应十进制为0，对应S2盒第1行。（每个S盒4行16列，注意数字从0开始：0~3，0~15）S1:0 行 0 列：14－－1110。S4:1 行 0 列：13－－1101。S2:0 行 8 列：9－－1001。S3:0 行 2 列：9－－1001。S5:0 行 0 列：2－－0010。S6:0 行 8 列：0－－0000。S7:0 行 2 列：2－－0010。S8:0 行 1 列：2－－0010。
算法之十进制转换成二进制
Y673582465的专栏
06-07 646
#define bits(x) sizeof(x)*8void decToBin(short x) { int temp[bits(x)]; int num = bits(x); if(x < 0) { x = -x; printf("-"); } for(int i = 0; i < num; i++) {
Python 中DES解密，16进制转2进制
kunpengku
12-15 2514
事情是这样的. 有一个 外部 域名 的接口A ，我自己也在本地提供了一个 php的服务 B，这个php里调用的就是 A，  然后我用 Python去调用 接口B，好慢好慢。 知道我用Pyhon直接去urllib直接调用A 。真的好快 。 不知道为什么 。中间隔了一层 竟然会这么慢。 以后不再这么弄了。  又是 贪小便宜 。 原因是 对方过来的数据是DES加密的。我用php解密了一次，
对称密码之DES
Learning
12-12 900
1、对称密码的概念       1.加密密钥和解密密钥相同，对于大多数对称密码算法，加解密过程互逆       2.加解密通信模型                  3.特点：算法公开、计算量小、加密速度快、加密效率高       4.弱点：双方都使用同样密钥，安全性得不到保证 2、常见的对称加密方式       （1）DES   （Data Encryption Standar
信息安全概论复习笔记 第五章 对称密码des算法
csdncaozhenming的博客
04-21 1770
信息安全概论复习笔记 第五章 对称密码des算法
密码学之DES算法
零度°C的博客
08-19 3865
DES（Data Encryption Standard），即数据加密标准，是一种广泛使用的对称密钥加密算法。它是由IBM在20世纪70年代初期设计，并在1977年被美国国家标准局（NBS，现国家标准与技术研究院NIST）正式采纳为联邦信息处理标准（FIPS）。DES算法使用56位密钥对64位的数据块进行加密，产生64位的密文。其加密过程包括初始置换、16轮迭代的Feistel网络、以及最终的逆置换。
密码学【第三节：对称密码-DES\AES】
尽欢
09-19 733
DES加密算法、AES加密算法、DES与AES加密算法的区别比较、加密解密工具推荐
密码学 | 对称加密算法DES
爬虫进击之路
10-12 2450
DES全称为Data Encryption Standard，是一种对称密钥的分组加密算法。DES加密、解密用的密钥是一样的所有称之为对称密钥。这种算法在加密的过程中会把明文划分为很多个等长的块(block)，然后对每个块进行加密，最后把所有的块拼在一起。也可以称之为“块加密”。
密码学之DES密码
weixin_43699616的博客
11-18 1850
DES密码是比较重要的对称加密算法，使用了移位、分组、置换等多种加密方法。 DES加密过程 S={P,C,K,E,D}，其中明文P，密文C是64bit的数据，密钥K是56bit的数据 1.明文首先经过一次置换（IP），置换后还是64bit。 2.将置换后的明文分为两部分：L，R，分别的32bit。然后与k作用，经过16圈的迭代。此时的k1…k16经过去除奇偶校验位等后变成48bit。其通用公式为...
对称密码及案例
qq_31639829的博客
10-29 5335
1. 概述 1.1概念 根据密钥的使用方式，可以将密码分为对称密码和非对称密码（公钥密码）。 对称密码（symmetric cryptography）是指在加密和解密时使用同一密钥的方式。而公钥密码（public key cryptography）则是在加密和解密时使用不同的密钥。 常用的对称密码有：DES、3DES、AES等等。 1.2 特性 加密和解密使用同一个密钥 加密和解密速度较快，适合加密比较大的数据 密钥传递的过程不安全，而且容易被破解，密钥管理也比较麻烦 2. DES 2.1 介绍 DES
对称密码之DES实验源代码
05-05
输入密钥和明文，明文先进行初始变换，分为左右两半L0和R0，各32位长，R0放入扩展函数E，扩展成48位；密钥k进行置换选择PC1，密钥中每个第8 位都用作奇偶校验，故有效密钥长度是56位，分为左右两半，各为28位，分别...
密码学实验_对称加密算法DES_非对称加密算法RSA.pdf
02-20
本实验报告主要涉及两种加密算法：对称加密算法DES（Data Encryption Standard）和非对称加密算法RSA。实验旨在帮助学生深入理解这两种算法的基本原理，并通过Python编程实现加密和解密过程。 ### **对称加密算法...
DES.zip_DES加密_对称加密算法_对称密码算法
09-22
在"DES.zip_DES加密_对称加密算法_对称密码算法"的压缩包中，可能包含了关于DES加密算法的详细解释、示例代码或程序实现，以及可能的测试数据。学习和理解DES，不仅可以了解对称加密的基本原理，也能为理解和使用更...
Des.rar_对称密码_对称密码算法
09-14
DES算法为密码体制中的对称密码体制，又被成为美国数据加密标准，是1972年美国IBM公司研制的对称密码体制加密算法。
基于对称密码技术的DES算法
11-13
通过对称密码技术的DES算法实现通信。des对称加密，对称加密，是一种比较传统的加密方式，其加密运算、解密运算使用的是同样的密钥，信息的发送者和信息的接收者在进行信息的传输与处理时，必须共同持有该密码(称为...
深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法
JakeMa1024的博客
06-06 1091
在现代 Web 开发中，随机数的生成看似简单，却隐藏着许多玄机。无论是生成密码、加密密钥，还是创建安全令牌，随机数的质量直接关系到系统的安全性。JavaScript 提供了多种生成随机数的方法，而其中 **`window.crypto.getRandomValues()`** 是最值得开发者关注的高安全方案。本文将深入解析这一方法的原理、用法和适用场景，帮助你更好地理解其背后的技术逻辑。
[密码学实战]C语言使用SDF库构建国密算法RESTful服务（五）
曼岛_的博客
06-06 309
[密码学实战]C语言使用SDF库构建国密算法RESTful服务（五）
python数据结构和算法(5)
最新发布
编码小栈
06-11 177
插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中，从而得到一个新的，个数加一的有序数据，算法适用于少量数据的排序。
加法c++
D_31415926的博客
06-06 390
给定 a 和 b 分别作为被加数和加数，而且限定 a 是 4 位数字，b 是 3 位数字，都是正整数。请你模拟以上加法过程进行输出。如果最后 a+b 的结果是 5 位数，为了保证对齐，需要在被加数和加数前面加空格。只需判断a+b的位数（注：四位数+三位数只可能是四位数或五位数，因为1000+100=1100，9999+999=10998），当a+b为四位数或五位数时输出特定的格式即可。输入两个正整数 a 和 b。
三重DES加密分析与对称密码体制
"本文主要探讨了对称密码体制中的一个重要变种——双密钥的三重DES，并介绍了分组密码的基本原理，包括DES和AES，以及分组密码的工作模式。" 双密钥的三重DES是一种增强版的DES加密算法，它通过使用两个不同的密钥...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值