学习记录
文章目录
原题位置:https://atcoder.jp/contests/abc404
A Not Found 2 sec 1024 MB Submit
题目:将字符串的字符用数组存储,出现则计次,最后输出计次为0的字符即可
#include<bits/stdc++.h>
using namespace std;
int main(){
string s;
cin >> s;
vector<int> v(27 , 0);
for(auto i : s){
v[i - 'a']++;
}
for(int i = 0; i <= 27;i ++){
if(v[i] == 0){
printf("%c" , i + 'a');
return 0;
}
}
}
B Grid Rotation 2 sec 1024 MB Submit
题目给的是两张二维网格s 和 t ,每个网格都有颜色,为白色或者黑色,要求是通过不限次数的 将s表整体顺时针旋转90度 和 将网格颜色反转 这两个操作来把 s 表变成 t 表,要求次数尽可能少
解题:操作:要么旋转,要么改色, 那就有三种搭配,
· 多次旋转 多次改色 11122222
· 多次改色 多次旋转 22211111
· 改色 和 旋转 混搭 12121212121221
显而易见,3 排除, 混搭变数很多, 那么分类计算旋转不同角度后的改色次数,最少的就是答案
将数据读入二维数组 s 和 t 中,再对比旋转后的s表和t表,计次,最后输出最小值
由于旋转操作也算入计次,所以代码中的cnt表有初始值
#include<bits/stdc++.h>
using namespace std;
int main(){
int N;
cin >> N;
//s t 表
vector<vector<char>> s(N + 1 , vector<char>(N + 1)) , t(N + 1 , vector<char>(N + 1));
//这里使用cnt数组来存储不同旋转角度的改色次数
vector<int> cnt = {0 , 1 , 2 , 3};
for(int i = 1;i <= N;i++){
for(int j = 1;j <= N;j++){
cin >> s[i][j];
}
}
for(int i = 1;i <= N;i++){
for(int j = 1;j <= N;j++){
cin >> t[i][j];
}
}
//不旋转
for(int i = 1;i <= N;i++){
for(int j = 1;j <= N;j++){
if(s[i][j] != t[i][j]){
cnt[0]++;
}
// cout << s[i][j];
}
// cout << endl;
}
//90
for(int i = 1;i <= N;i++){
for(int j = N , k = 1;j >= 1 , k <= N;j-- , k++){
if(s[j][i] != t[i][k]){
cnt[1]++;
}
// cout << s[j][i];
}
// cout << endl;
}
//180
for(int i = N , k = 1;i >= 1 , k <= N;i-- , k++){
for(int j = N , m = 1;j >= 1 , m <= N;j-- , m++){
if(s[i][j] != t[k][m]){
cnt[2]++;
}
}
}
//270
for(int i = N , k = 1;i >= 1 , k <= N;i-- , k++){
for(int j = 1;j <= N;j++){
if(s[j][i] != t[k][j]){
cnt[3]++;
}
}
}
cout << *min_element(cnt.begin() , cnt.end());
return 0;
}
C Cycle Graph? 2 sec 1024 MB Submit
这题的话,给了一张图的信息,判断图是否是循环图,循环图点和边数量相同,并且每个点的度数为2,循环图必然是连通的,所以dfs或者bfs走一遍,那么每个点和边都可以走到,稠密图用bfs,稀疏图用dfs,再看N和M的范围,所以选择bfs解题
#include<bits/stdc++.h>
using namespace std;
int main(){
int n , m;
cin >> n >> m;
if(n != m){
cout << "No" << endl;
return 0;
}
vector<vector<int>> vv(n);
vector<int> cnt(n , 0);
for(int i = 1;i <= m;i++){
int x , y;
cin >> x >> y;
x--;
y--;
vv[x].push_back(y);
vv[y].push_back(x);
cnt[x]++;
cnt[y]++;
}
for(int i : cnt){
if(i != 2){
cout << "No" << endl;
return 0;
}
}
vector<bool> vst(n , false);
queue<int> q;
q.push(0);
vst[0] = true;
int cnt2 = 1;
while(!q.empty()){
int u = q.front();
q.pop();
for(int v : vv[u]){
if(!vst[v]){
vst[v] = true;
q.push(v);
cnt2++;
}
}
}
if(cnt2 == n){
cout << "Yes" << endl;
}else{
cout << "No" << endl;
}
return 0;
}
D Goin’ to the Zoo 2 sec 1024 MB Submit
题意:给了N个动物园,又给了M个想看的动物,后面的数据是告诉我们每只想看的动物在哪些动物园里面可以看,例如下面给的样例:
4 3
1000 300 700 200
3 1 3 4
3 1 2 4
2 1 3
这里面的3 1 3 4是第一行,所以这第一行的数据表示M个想看的动物里面的第一个想看的动物的数据,是有3个动物园可以看到,分别是 1号,3号,4号动物园;
解题:N最大为10,每一种动物园有三种去法,为0 , 1 ,2次,多于2次就是浪费钱了,暴力枚举的时间复杂度计算大约为O(3^N ),尝试暴力枚举解题;
代码思路:
先获取数据,将数据存储好,对于jz[]数组,是进制,里面存的是3的每个次方的数据,方便后面使用;
对于主要遍历部分,思路:从0开始,一直到3^N,所有的可能都走一遍,创建一个amlcnt数组,里面是每个动物被访问次数的记录,仅仅用于本次循环,因为后面判断每个动物是否被访问两次,true才算成功,最后与上一次循环得出的费用比较,取低的值。
for(int i = 1;i <= N;i++){
int tm = cnt / jz[i - 1] % 3;
这段代码的意思是对于每个动物园,我们都把他看成一个数数,然后这个数一个三进制,int tm = cnt / jz[i - 1] % 3;是用于求每个三进制对应的值,所以主要思想是将遍历看成三进制数字,这是一种位运算思想,因为每个动物园只能去三次,所以可以看成三进制,再进行遍历,这样子的遍历是每次都有的,不会漏,就像从1数到100,每个数字都会数到,只不过这里是三进制的数数,从0数到3^N,每次数数的时候都计算一次费用。
#include<bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(0) , cin.tie(0);
// freopen("cpptest.txt" , "r" , stdin);
int N , M;
cin >> N >> M;
vector<int> cost(N+1);
for(int i = 1;i <= N;i++){
cin >> cost[i];
}
vector<int> jz(N + 1);
jz[0] = 1;
for(int i = 1;i <= N;i++){
jz[i] = pow(3 , i);
}
vector<vector<int>> zoo(N+1);
for(int i = 1;i <= M;i++){
int t; cin >> t;
for(int j = 0;j < t;j ++){
int x; cin >> x;
zoo[x].push_back(i);
}
}
long long ret = 1e18;
for(int cnt = 0;cnt < jz[N];cnt++){
vector<int> amlcnt(M + 1 , 0);
long long tcost = 0;
for(int i = 1;i <= N;i++){
int tm = cnt / jz[i - 1] % 3;
tcost += tm * cost[i];
for(int j = 0;j < tm;j++){
for(int taml: zoo[i]){
amlcnt[taml]++;
}
}
}
bool tbl = true;
for(int i = 1;i <= M;i++){
if(amlcnt[i] < 2){
tbl = false;
break;
}
}
if(tbl == true){
ret = min(tcost , ret);
}
}
cout << ret << endl;
return 0;
}
G Specified Range Sums 2 sec 1024 MB Submit
题意:给了三个正整数序列,需要我们求一个A序列,这个A序列如果不存在则输出-1,A序列满足下面的要求:
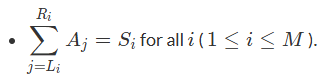
题目中的N是对序列的长度要求,M是给出的三个序列的长度,上面的这个公式解释:
我们看样例1:
5 3
1 2 4
2 3 5
5 5 5
那么L:1 2 5
R:2 3 5
M:4 5 5
对于范围内的i,代入求和公式,
当i = 1时,L1 = 1 , R1 = 2,所以区间为【1,2】那么Aj = A1 + A2 = S1 = 4
当i = 2时,L2 = 2 , R2 = 3,所以区间为【2,3】那么Aj = A2 + A3 = S2 = 5
当i = 3时,L3 = 5 , R3 = 5,所以区间为【5,5】那么Aj = A5 = 5
所以我们可以求A1 , A2 , A3 ,A5,题目要去A序列有5个,并且A序列求和要偏小,而序列都是正整数序列,所以我们A4给1作为他的值。
A1 + A2 = 4
A2 + A3 = 5
A5 = 5
那么有下面几种可能:
A1 A2 A3 A4 A5
1 3 2 1 5
2 2 3 1 5
3 1 4 1 5
求和下来,最上面的那个种和最小,为12,所以答案为12,
所以这道题目就变成了对一组不等式求解的问题,我们可以使用差分约束系统,那么就成了一道差分约束的模板题
#include<bits/stdc++.h>
using namespace std;
struct Edge {
int from, to;
long long w;
};
bool bellmanFord(int n, const vector<Edge>& e, vector<long long>& d) {
d.assign(n + 1, LLONG_MAX);
d[0] = 0;
for (int i = 0; i < n; ++i) {
for (const Edge& edge : e) {
if (d[edge.from] != LLONG_MAX && d[edge.from] + edge.w < d[edge.to]) {
d[edge.to] = d[edge.from] + edge.w;
}
}
}
for (const Edge& edge : e) {
if (d[edge.from] != LLONG_MAX && d[edge.from] + edge.w < d[edge.to]) {
return false;
}
}
return true;
}
int main() {
int n, m;
cin >> n >> m;
vector<Edge> e;
for (int i = 0;i < m;i++) {
int l, r;
long long s;
cin >> l >> r >> s;
e.push_back({l - 1, r, -s});
e.push_back({r, l - 1, s});
}
for (int j = 1; j <= n; ++j) {
e.push_back({j - 1, j, -1});
}
vector<long long> d;
if (!bellmanFord(n, e, d)) {
cout << -1 << endl;
} else {
cout << -d[n] << endl;
}
return 0;
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








