3.16代码随想录第十八天打卡

669. 修剪二叉搜索树

(1)题目描述:

(2)解题思路:

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr ) return nullptr;
        if (root->val < low) {
            TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
            return right;
        }
        if (root->val > high) {
            TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
            return left;
        }
        root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
        root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
        return root;
    }
};

(3)总结:

1.当前节点数若小于左边界，当前节点及其左子树均删除，只需对其右子树进行递归查找
2.当前节点数若大于右边界，当前节点及其右子树均删除，只需对其左子树进行递归查找

108.将有序数组转换为二叉搜索树

(1)题目描述:

(2)解题思路:

class Solution {
private:
    TreeNode* traversal(vector<int>& nums, int left, int right) {
        if (left > right) return nullptr;
        int mid = left + ((right - left) / 2);
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = traversal(nums, left, mid - 1);
        root->right = traversal(nums, mid + 1, right);
        return root;
    }
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        TreeNode* root = traversal(nums, 0, nums.size() - 1);
        return root;
    }
};

(3)总结:

1.注意是构造平衡二叉搜索数

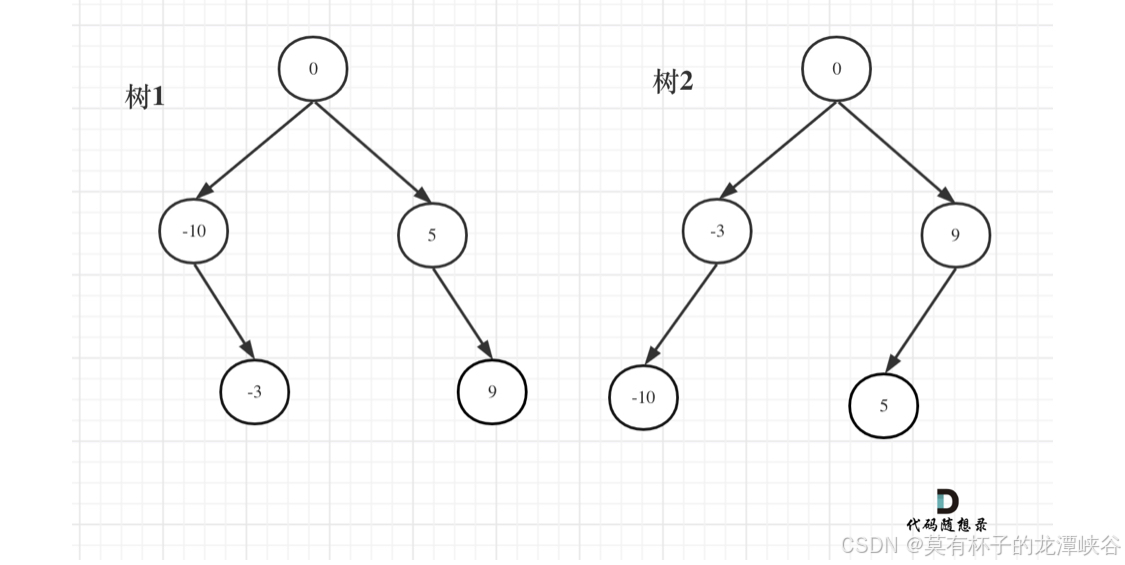
2.数组中数为奇数时取中间的数0作为二叉树的根节点，以0为分界左右分为两个数组，当数组长度为偶数时，从这个数组的左右开始都可以写出二叉数，只是构造出的二叉树结构会略有不同

3.递归时参数如果不用引用，将重复的copy内存空间，会造成程序的性能很差

4.在调用traversal的时候传入的left和right为什么是0和nums.size() - 1，因为定义的区间为左闭右闭。

 538.把二叉搜索树转换为累加树

(1)题目描述:

(2)解题思路:

class Solution {
private:
    int pre = 0; // 记录前一个节点的数值
    void traversal(TreeNode* cur) { // 右中左遍历
        if (cur == NULL) return;
        traversal(cur->right);
        cur->val += pre;
        pre = cur->val;
        traversal(cur->left);
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        pre = 0;
        traversal(root);
        return root;
    }
};

(3)总结:

1.要从大到小遍历是右中左，累加前一个结点的数值用双指针法