一日攻克十大经典排序算法（1)

一，冒泡排序 

1.算法步骤

比较相邻元素：从列表的第一个元素开始，比较相邻的两个元素。

交换位置：如果前一个元素比后一个元素大，则交换它们的位置。

重复遍历：对列表中的每一对相邻元素重复上述步骤，直到列表的末尾。这样，最大的元素会被"冒泡"到列表的最后。

缩小范围：忽略已经排序好的最后一个元素，重复上述步骤，直到整个列表排序完成。

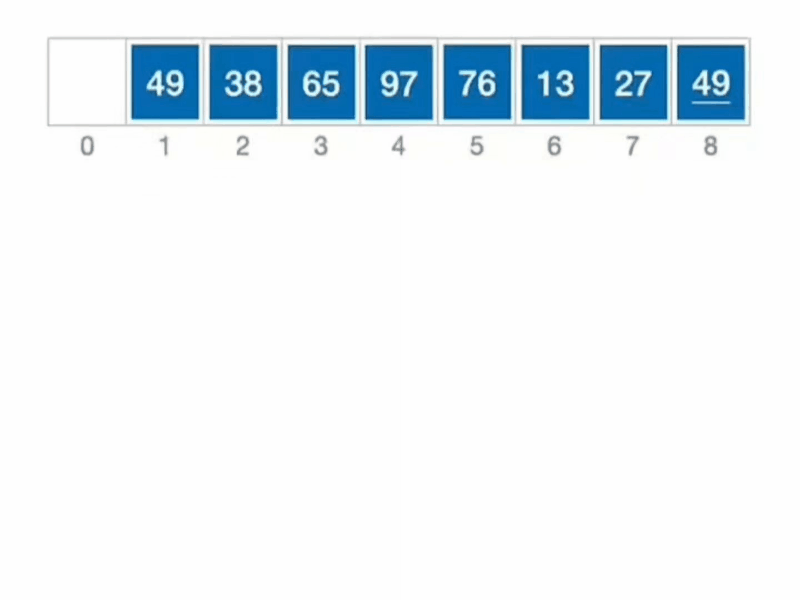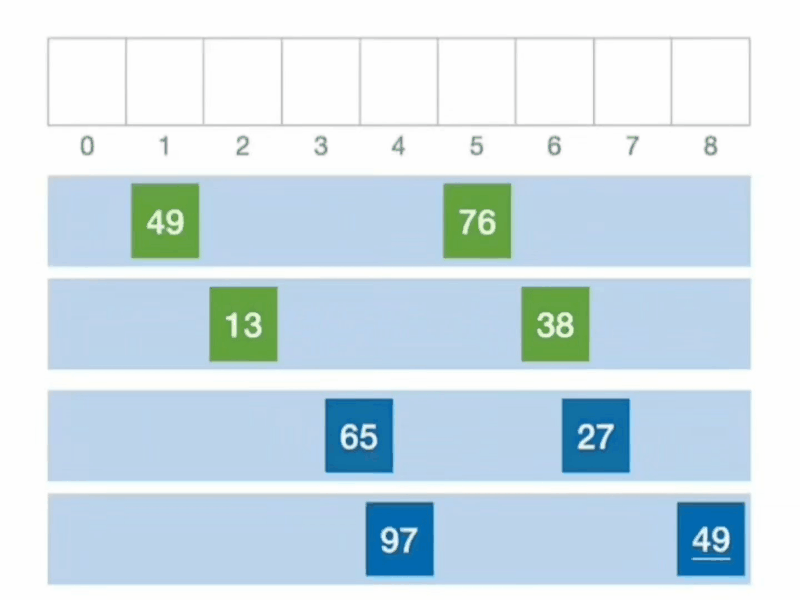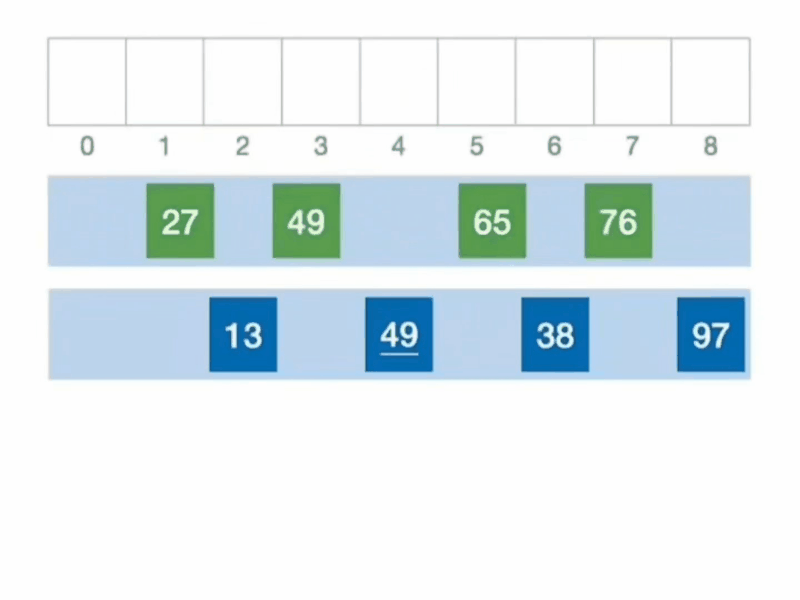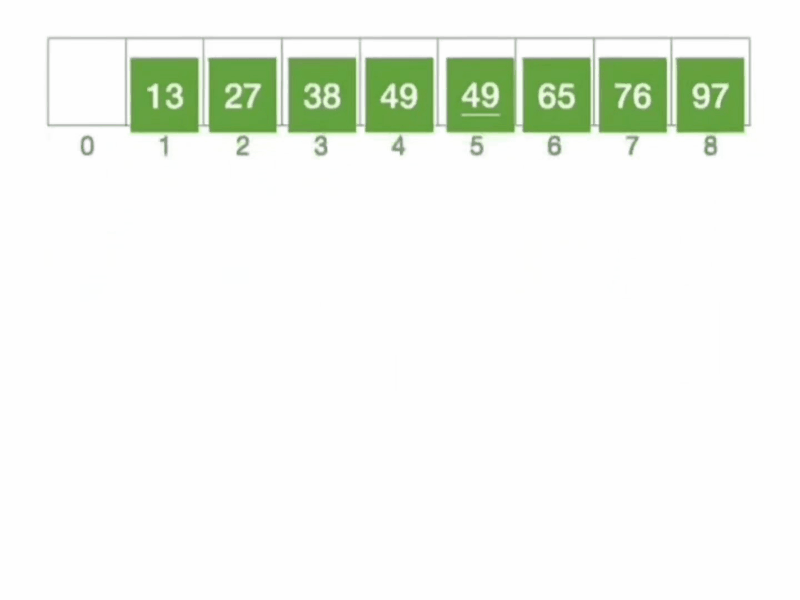
2.动画演示

3.具体示例 

假设有一个待排序的列表 [8，39，14，56，1]，冒泡排序的过程如下：

1. 第一轮遍历：

   • 比较 8 和 39，不交换。

   • 比较 39 和 14，交换位置，列表变为 [8, 14, 39, 56, 1]。

   • 比较 39 和 56，不交换。

   • 比较 56 和 1，交换位置，列表变为 [8, 14, 39, 1, 56]。

   • 第一轮结束后，最大的元素 56 已经"冒泡"到列表的最后。

2. 第二轮遍历：

   • 比较 8 和 14，不交换。

   • 比较 14 和 39，不交换。

   • 比较 39 和 1，交换位置，列表变为 [8, 14, 1, 39, 56]。

   • 第二轮结束后，第二大的元素 39 已经"冒泡"到列表的倒数第二位置。

3. 第三轮遍历：

   • 比较 8 和 14，不交换。

   • 比较 14 和 1，交换位置，列表变为 [8, 1, 14, 39, 56]。

   • 第三轮结束后，第三大的元素 14 已经"冒泡"到列表的倒数第三位置。

4. 第四轮遍历：

   • 比较 8 和 1，交换位置，列表变为 [1, 8, 14, 39, 56]。

   • 列表已经完全有序。

4.代码实现

#include <iostream>
using namespace std;
void bubble_sort(int arr[], int len) {
        int i, j, temp;
        for (i = 0; i < len - 1; i++)
                for (j = 0; j < len - 1 - i; j++)
                        if (arr[j] > arr[j + 1]) {
                                temp = arr[j];
                                arr[j] = arr[j + 1];
                                arr[j + 1] = temp;
                        }
}
int main() {
        int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
        //sizeof(arr) 会返回整个数组占用的内存大小。sizeof(arr[0]) 会返回数组中单个元素占用的内存大小。
        int len = sizeof(arr) / sizeof(arr[0]); //两者相除，得到的就是数组的长度。
        bubble_sort(arr, len);
        int i;
        for (i = 0; i < len; i++)
                cout<<arr[i]<<"\t";
        return 0;
}

二，选择排序 

1.算法步骤

初始化：将列表分为已排序部分和未排序部分。初始时，已排序部分为空，未排序部分为整个列表。

查找最小值：在未排序部分中查找最小的元素。

交换位置：将找到的最小元素与未排序部分的第一个元素交换位置。

更新范围：将未排序部分的起始位置向后移动一位，扩大已排序部分的范围。

重复步骤：重复上述步骤，直到未排序部分为空，列表完全有序。

2.动画演示

3.具体实例

假设有一个待排序的列表 [58, 32, 12, 18, 6]，选择排序的过程如下：

1. 第一轮：

   • 未排序部分：[58, 32, 12, 18, 6]。

   • 找到最小值 6，将其与第一个元素 58 交换。

   • 列表变为 [6，18, 32, 12, 58]。

   • 已排序部分：[6]，未排序部分：[32, 12, 18, 58]。

2. 第二轮：

   • 未排序部分：[32, 12, 18, 58]。

   • 找到最小值 12，将其与第一个元素 32 交换。

   • 列表变为 [6, 12, 32, 18, 58]。

   • 已排序部分：[6, 12]，未排序部分：[32, 18, 58]。

3. 第三轮：

   • 未排序部分：[32, 18, 58]。

   • 找到最小值 18，将其与第一个元素 32 交换。

   • 列表变为 [6, 12, 18, 32, 58]。

   • 已排序部分：[6, 12, 18]，未排序部分：[32, 58]。

4. 第四轮：

   • 未排序部分：[32, 58]。

   • 找到最小值 32，它已经在正确的位置，无需交换。

   • 列表保持不变：[6, 12, 18, 32, 58]。

   • 已排序部分：[6, 12, 18, 32]，未排序部分：[58]。

5. 第五轮：

   • 未排序部分：[58]。

   • 只有一个元素，无需操作。

   • 列表完全有序：[6, 12, 18, 32, 58]。

4.代码实现

void swap(int *a,int *b) 
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
void selection_sort(int arr[], int len) 
{
    int i,j;

        for (i = 0 ; i < len - 1 ; i++) 
    {
                int min = i;
                for (j = i + 1; j < len; j++)     //走访未排序的元素
                        if (arr[j] < arr[min])    //找到未排序中最小值
                                min = j;    //记录最小值
                swap(&arr[min], &arr[i]);    //将未排序中第一个数与最小值做交換
        }
}

三，插入排序 

1.算法步骤

初始化：将列表分为已排序部分和未排序部分。初始时，已排序部分只包含第一个元素，未排序部分包含剩余元素。

选择元素：从未排序部分中取出第一个元素。

插入到已排序部分：将该元素与已排序部分的元素从后向前依次比较，找到合适的位置插入。

重复步骤：重复上述步骤，直到未排序部分为空，列表完全有序。

2.动画演示

3.具体实例

 假设有一个待排序的列表 [46, 28, 31, 78, 18, 20]，插入排序的过程如下：

1. 初始状态：

   • 已排序部分：[46]。

   • 未排序部分： [28, 31, 78, 18, 20]。

2. 第一轮：

   • 取出未排序部分的第一个元素 28。

   • 将 28 与已排序部分的 46 比较，28<46，插入到 5 前面。

   • 列表变为  [ 28,46, 31, 78, 18, 20]。

   • 已排序部分： [ 28,46]，未排序部分： [31, 78, 18, 20]。

3. 第二轮：

   • 取出未排序部分的第一个元素 31。

   • 将 31与已排序部分的 46 比较，31<46，继续与 28比较，31>28，插入到 28 和 46之间。

   • 列表变为 [ 28,31,46, 78, 18, 20]。

   • 已排序部分：[ 28,31,46 ]，未排序部分：[  78, 18, 20]。

4. 第三轮：

   • 取出未排序部分的第一个元素 78。

   • 将 78 与已排序部分的 46 比较，78>46，直接插入到末尾。

   • 列表变为 [ 28,31,46, 78, 18, 20]。

   • 已排序部分：[ 28,31,46, 78 ]，未排序部分：[ 18, 20]。

5. 第四轮：

   • 取出未排序部分的第一个元素 18。

   • 将 18 与已排序部分的 78 比较，18 < 78，继续与 46、31、28 比较，18 是最小的，插入到最前面。

   • 列表变为 [ 18,28,31,46, 78, 20]。

   • 已排序部分：[ 18,28,31,46, 78]，未排序部分：[20]。

6. 第五轮：

   • 取出未排序部分的第一个元素 20。

   • 将 20 与已排序部分的 78 比较，20<78 ，继续与 46、31、28 比较，20>18 ，插入到 18 和 28 之间。

   • 列表变为 [ 18, 20,28,31,46, 78]。

   • 已排序部分： [ 18, 20,28,31,46, 78]，未排序部分为空。

4.代码实现

#include <iostream>
using namespace std;
void insertion_sort(int arr[],int len){
        for(int i=1;i<len;i++){
                int key=arr[i]; //取出未排序中的第一个元素
                int j=i-1;
                //将key插入已排序部分的正确位置
                while((j>=0) && (key<arr[j])){
                        arr[j+1]=arr[j]; //向后移动元素
                        j--;
                }
                arr[j+1]=key;  //插入key
        }
}
int main() {
        int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
        int len = sizeof(arr) / sizeof(arr[0]);
        insertion_sort(arr, len);
        int i;
        for (i = 0; i < len; i++)
                cout<<arr[i]<<"\t";
        return 0;
}

四，希尔排序

1.算法步骤

选择增量序列：选择一个增量序列（gap sequence），用于将列表分成若干子列表。常见的增量序列有希尔增量（n/2, n/4, ..., 1）等。

分组插入排序：按照增量序列将列表分成若干子列表，对每个子列表进行插入排序。

缩小增量：逐步缩小增量，重复上述分组和排序过程，直到增量为 1。

最终排序：当增量为 1 时，对整个列表进行一次插入排序，完成排序。

2.动画演示

3.具体实例

假设有一个待排序的列表 [8, 3, 1, 2, 7, 5, 6, 4]，使用希尔增量（初始增量为 n/2），排序过程如下：

1. 初始状态：

   • 列表：[8, 3, 1, 2, 7, 5, 6, 4]。

   • 初始增量：4（列表长度 8 的一半）。

2. 第一轮（增量为 4）：

   • 将列表分成 4 个子列表：                                  2.对每个子列表进行插入排序：

     • 子列表 1：[8, 7]。                                          1.子列表 1：[7, 8]。

     • 子列表 2：[3, 5]。                                           2.子列表 2：[3, 5]。

     • 子列表 3：[1, 6]。                                           3.子列表 3：[1, 6]。

     • 子列表 4：[2, 4]。                                           4.子列表 4：[2, 4]。 

                 排序后的列表：[7, 3, 1, 2, 8, 5, 6, 4]。 

    3. 第二轮（增量为 2）：

              1. 将列表分成 2 个子列表：                                   2.对每个子列表进行插入排序：

                      1. 子列表 1：[7, 1, 8, 6]。                                  1. 子列表 1：[1, 6, 7, 8]。

                       2. 子列表 2：[3, 2, 5, 4]。                                 2. 子列表 2：[2, 3, 4, 5]。

         排序后的列表：[1, 2, 6, 3, 7, 4, 8, 5]。

    4. 第三轮（增量为 1）：

              1. 将整个列表视为一个子列表，进行插入排序。

              2.排序后的列表：[1, 2, 3, 4, 5, 6, 7, 8]。

4.代码实现

void shell_sort(int arr[], int len) {
        int d, i, j;
        for(d=n/2; d>=1; d=d/2)
            for (i = d+1; i <= n; ++i) 
                if(arr[i]<arr[i-d]){
                    arr[0]=arr[i];
                        for (j = i - d; j >= 0 && arr[j] > arr[0]; j -= d)
                                arr[j + d] = arr[j];
                        arr[j + d] = arr[0];
                }
}

五，归并排序

1.算法步骤

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；

3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

4. 重复步骤 3 直到某一指针达到序列尾；

5. 将另一序列剩下的所有元素直接复制到合并序列尾

2.动画演示

3.具体实例

假设有一个待排序的列表 [38, 27, 43, 3, 9, 82, 10]，归并排序的过程如下：

1. 分解：

   • 将列表分成两半：[38, 27, 43, 3] 和 [9, 82, 10]。

   • 继续分解：

     • [38, 27, 43, 3] 分成 [38, 27] 和 [43, 3]。

     • [9, 82, 10] 分成 [9] 和 [82, 10]。

   • 继续分解：

     • [38, 27] 分成 [38] 和 [27]。

     • [43, 3] 分成 [43] 和 [3]。

     • [82, 10] 分成 [82] 和 [10]。

   • 最终分解为单个元素的子列表。

2. 合并：

   • 合并 [38] 和 [27] 得到 [27, 38]。

   • 合并 [43] 和 [3] 得到 [3, 43]。

   • 合并 [27, 38] 和 [3, 43] 得到 [3, 27, 38, 43]。

   • 合并 [9] 和 [10, 82] 得到 [9, 10, 82]。

   • 合并 [3, 27, 38, 43] 和 [9, 10, 82] 得到最终有序列表 [3, 9, 10, 27, 38, 43, 82]。

4.代码实现

int min(int x, int y) {
    return x < y ? x : y;
}
void merge_sort(int arr[], int len) {
    int *a = arr;
    int *b = (int *) malloc(len * sizeof(int));
    int seg, start;
    for (seg = 1; seg < len; seg += seg) {
        for (start = 0; start < len; start += seg * 2) {
            int low = start, mid = min(start + seg, len), high = min(start + seg * 2, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        int *temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        int i;
        for (i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    free(b);
}